Andhra Pradesh SSC Board Question Paper for Class 10th Maths Paper 1 2019 In PDF

AP SSC or 10th Class Question Paper Mathematics Paper 1 English Medium 2019 with Solutions – Free Download

Andhra Pradesh SSC (Class 10) Maths 2019 question paper 1 with solutions are available here in a downloadable pdf format and also in the text so that the students can easily make use of them. Along with the solutions, they can also get the Maths question paper 1 2019 Class 10 SSC for reference. Students are able to access all the Andhra Pradesh board previous year maths question papers here. AP 10th Class Mathematics Question Paper 2019 Paper 1 with Solutions can be downloaded easily and students can solve and verify the answers provided by BYJU’S. Solving 2019 Maths question paper 1 for Class 10 will help the students to predict what type of questions will appear in the exam.

Download SSC 2019 Question Paper Maths Paper 1

Download SSC 2019 Question Paper Maths Paper 1 With Solutions

Andhra Pradesh SSC Class 10th Maths Question Paper 1 With Solution 2019

QUESTION PAPER CODE 15E(A)

SECTION – I

(4 * 1 = 4)

Question 1: Write A = {2, 4, 8, 16} in set-builder form.

Solution:

A = {2ⁿ / n ∈ N, and n < 5}

Question 2: Find the value of log₅ √625.

Solution:

log₅ √625

= log₅ 25

= log₅ 5²

= 2 log₅ 5

= 2 * 1

= 2

Question 3: The larger of two supplementary angles exceeds the smaller by 58^o, then find the angles.

Solution:

Let the required supplementary angles be x and y.

x + y = 180^o —- (1)

The larger angle exceeds the smaller by 58^o.

x – y = 58^o —- (2)

Solve (1) and (2),

2x = 238

x = 238 / 2

x = 119^o

y = 61^o

Question 4: Find the curved surface area of the cylinder, whose radius is 7cm and height is 10cm.

Solution:

Radius if the cylinder (r) = 7cm

Height of the cylinder (h) = 10cm

The curved surface area of the cylinder = 2𝛑rh

= 2 * (22 / 7) * (7) * (10)

= 440 cm²

SECTION – II

(5 * 2 = 10)

Question 5: Rohan’s mother is 26 years older than him. The product of their ages after 3 years will be 360. Then write the required quadratic equation to find Rohan’s present age.

Solution:

Let Rohan’s present age be x years.

His mother’s age at present is (x + 26) years.

After 3 years, Rohan’s age = (x + 3) years

After 3 years, his mother’s age = (x + 26) + 3 = (x + 29) years

The product of their ages = (x + 3) (x + 29)

= x * x + x * 29 + 3 * x + 3 * 29

= x² + 29x + 3x + 87

= x² + 32x + 87

By the sum, the product of their ages is 360

x² + 32x + 87 = 360

x² + 32x + 87 – 360 = 0

x² + 32x – 273 = 0 is the required quadratic equation.

Question 6: Find the zeroes of the quadratic polynomial x² – x – 30 and verify the relation between the zeroes and its coefficients.

Solution:

Given the polynomial x² – x – 30,

To find the zeros, x² – x – 30 = 0 [say]

= x² – 6x + 5x – 30

= x (x – 6) + 5 (x – 6)

= (x + 5) (x – 6)

x = -5 and x = 6

Sum of the zeroes = 6 + (-5)

= 1

= (-1) / 1

= – (coefficient of x) / (coefficient of x²)

Product of the zeroes = 6 (-5)

= -30

= (-30 / 1)

= (constant term) / (coefficient of x²)

Question 7: A joker’s cap is in the form of a right circular cone, whose base radius is 7cm and height is 24cm. Find the area of the sheet required to make 10 such caps.

Solution:

Base radius of the conical cap (r) = 7cm

Height (h) = 24cm

Slant height (l) = √r² + h²

= √7² + 24²

= √49 + 576

= √625

= 25 cm

Area of sheet required to make a cap = Lateral surface area of the cap

= 𝛑rl

= (22 / 7) * 7 * 25

= 550 sq.cm

Area of sheet required to 10 such caps

= 10 * 550

= 5500 sq.cm

Question 8: Find the HCF of 1260 and 1440 by using Euclid’s division lemma.

Solution:

The given numbers are 1260 and 1440.

1440 = 1260 * 1 + 180

1260 = 180 * 7 + 0

HCF of 1440 and 1260 is 180.

Question 9: If the sum of the first 15 terms of an AP is 675 and its first term is 10, then find 25^th term.

Solution:

First-term of an AP = a = 10

Let the common difference be d.

Sum of the first 15 terms is S₁₅ = 675

(15 / 2) = [2a + 14d] = 675

14d = 90 – 20 = 70

d = 70 / 14

d = 5

25^th term of an AP is a₂₅ = a + 24d

= 10 + 24 * 5

= 10 + 120

= 130

SECTION – III

(4 * 4 = 16)

Question 10:

[a] Show that 2 + 5√3 is irrational.

OR

[b] Check whether -321 is a term of the AP 22, 5, 8, 1…..

Solution:

2 + 5√3 = (a / b)

5√3 = (a / b) – 2

√3 = (a / 5b) – (2 / 5)

Since (a / 5b) and (2 / 5) ∈ Q, (a / 5b) – (2 / 5) ∈ Q.

So, √3 is rational.

But this contradicts the fact that √3 is irrational.

So, our assumption that 2 + 5√3 is rational is wrong.

So, 2 + 5√3 is irrational.

a = 22, d = -7

n^th term of an AP = a_n = a + (n – 1)d

In this AP, let the n^th term be -321

a + (n – 1)d = -321

22 + (n – 1) (-7) = -321

(n – 1) (-7) = -343

n – 1 = (-343) / (-7)

n = 49 + 1

n = 50

Hence, -321 will be the 50^th term in the given AP.

Question 11:

[a] In a class test, the sum of Moulika’s marks in mathematics and English is 30. If she got 2 marks more in mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in the two subjects.

OR

[b] An oil drum is in the shape of the cylinder, whose diameter is 2m and height is 7m. The painter charges Rs. 5 per m² to paint the drum. Find the total charges to be paid to the painter for 10 drums.

Solution:

Let the marks of Moulika in Mathematics be x and that of in English be 30 – x.

If she got 2 marks more in mathematics then marks in maths = x + 2

And she got 3 marks less in English then the marks in English = 30 – x – 3 = 27 – x

Product of these two = (x + 2) (27 – x) = 210

x² – 25x + 156 = 0

(x – 12) (x – 13) = 0

x = 12, 13

Case (i) If x = 12, the marks of Moulika in

Mathematics = 12

English = 30 – 12 = 18

Case (ii) If x = 13, the marks of Moulika in

Mathematics = 13

English = 30 – 13 = 17

The radius of the drum = r = d / 2 = 2 / 2 = 1m

Height = h = 7cm

Total surface area of the drum which is in the shape of cylinder = 2𝛑r (r + h)

= 2 * (22 / 7) * (1) * (1 + 7)

= 2 * (22 / 7) * 8

= 50.28 sq.m

Charges to paint the drum per sq.m = Rs. 5

The total cost of painting 10 such type of drums = 50.28 * 5 * 10 = Rs. 2514

Question 12:

(i) [a] If A = {x : x is a natural number less than is 6}.

B = {x : x is a prime number which is a divisor of 60}.

C = {x : x is an odd natural number less than 10}.

D = {x : x is an even natural number which is a divisor of 48}.

Then write the roster form for all the above sets and find

[a] A ⋃ B

[b] B ⋂ C

[c] A – D

[d] D – B

OR

(ii) 6 pencils and 4 notebooks together cost Rs. 90 whereas 8 pencils and 3 notebooks together cost Rs. 85. Find the cost of one pencil and that of one notebook.

Solution:

(i) [a] A = {1, 2, 3, 4, 5}

B = {2, 3, 5}

C = {1, 3, 5, 7, 9}

D = {2, 4, 6, 8, 12, 14, 16, 24, 48}

(ii) Let the cost of one pencil be Rs. x.

Cost of one notebook = Rs. y.

The total cost of 6 pencils and 4 notebooks = Rs. 90

6x + 4y = 90 —- (1)

The total cost of 8 pencils and 3 notebooks = Rs. 85

8x + 3y = 85 —- (2)

On solving the above two equations, x = 5, y = 15.

The cost of one pencil = Rs. 5

The cost of one notebook = Rs. 15

Question 13:

[a] Find the zeroes of the quadratic polynomial p(x) = x² + x – 20 using the graph.

OR

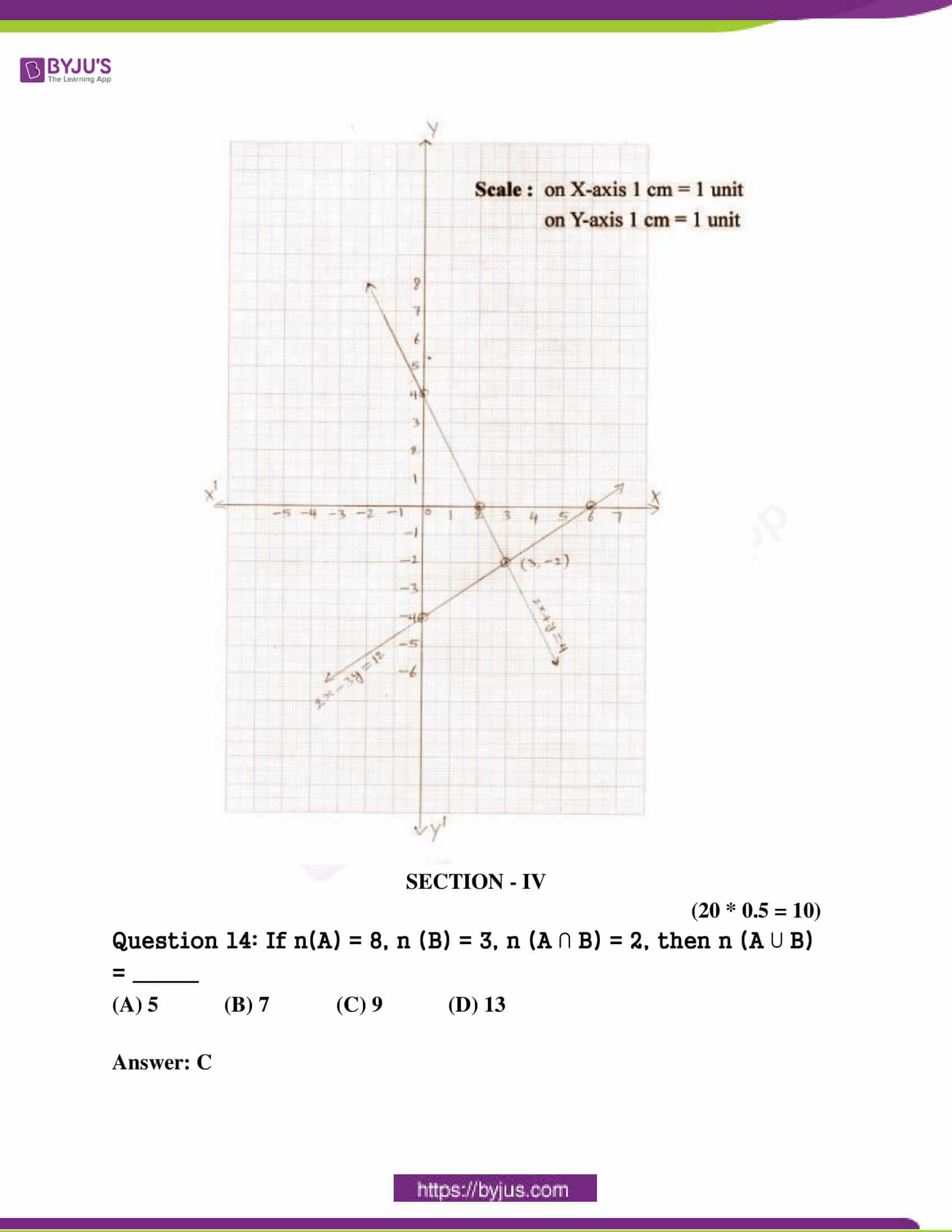
[b] Solve the following pair of linear equations graphically.

2x + y + 4 and 2x – 3y = 12.

Solution:

SECTION – IV

(20 * 0.5 = 10)

Question 14: If n(A) = 8, n (B) = 3, n (A ⋂ B) = 2, then n (A ⋃ B) = ______

(A) 5 (B) 7 (C) 9 (D) 13

Answer: C

Question 15: The discriminant of 6x² – 5x + 1 = 0 is ______

(A) 1 (B) 2 (C) 6 (D) (-5 / 6)

Answer: A

Question 16: Sum of the zeroes of the polynomial x² + 5x + 6 = 0 is

(A) 5 (B) -5 (C) 6 (D) (5 / 6)

Answer: B

Question 17: Which of the following is not irrational?

(A) √2 (B) √3 (C) √4 (D) √5

Answer: C

Question 18: One root of the equation x – (3 / x) = 2 is _____

(A) 1 (B) 2 (C) 3 (D) 4

Answer: C

Question 19: If 4, a, 9 are in GP, then a = ____

(A) 6 (B) ±6 (C) 7 (D) ±7

Answer: B

Question 20: If the total surface area of a cube is 96cm², then its volume is _____

(A) 32cm³ (B) 64 cm³ (C) 128cm³ (D) 256 cm³

Answer: B

Question 21: log ₁₀ 0.001 = _____

(A) 2 (B) 3 (C) -2 (D) -3

Answer: D

Question 22: Match the following.

If a, b, c are the zeroes of a cubic polynomial ax³ + bx² + cx + d = 0, then

[i] a + b + c [a] (-d / a)

[ii] ab + bc + ca [b] (c / a)

[iii] abc [c] (-b / a)

(A) [i] – c, [ii] – b, [iii] – a

(B) [i] – a, [ii] – b, [iii] – c

(C) [i] – b, [ii] – a, [iii] – c

(D) [i] – c, [ii] – a, [iii] – b

Answer: A

Question 23: The next term in AP √3, √12, √27, ……

(A) √32 (B) √36 (C) √42 (D) √48

Answer: D

Question 24: The shaded region in the figure shows

(A) A – B (B) B – A (C) μ – B (D) A ⋃ B

Answer: C

Question 25: 5x – 3 represents ______ polynomial.

(A) Linear (B) Quadratic (C) Cubic (D) Fourth degree

Answer: A

Question 26: The common difference in AP log₂ 2, log₂ 4, log₂ 8 …… is

(A) 1 (B) 2 (C) 3 (D) 4

Answer: A

Question 27: The sum of the first ‘n’ odd natural numbers is ______

(A) n (B) n² (C) n (n + 1) (D) n (n + 1) / 2

Answer: B

Question 28: The quadratic polynomial, whose zeroes are √2 and √-2 is ____

(A) x² – 2 (B) x² + 2 (C) x² + √2 (D) x – 2

Answer: A

Question 29: The number of zeroes of the polynomial in the graph is _____

(A) 0 (B) 1 (C) 2 (D) 3

Answer: D

Question 30: The line 2x – 3y = 8 intersects x-axis at

(A) (2, -3) (B) (0, -3) (C) (2, 0) (D) (4, 0)

Answer: D

Question 31: The volume of the cone, whose radius is 3cm and height is 8cm, is _____ cm³.

(A) 6𝛑 (B) 12𝛑 (C) 18𝛑 (D) 24𝛑

Answer: D

Question 32: If 6x + 2y + 9 = 0 and kx + y – 7 = 0 has no solution, then k = ______

(A) 3 (B) 2 (C) -3 (D) -2

Answer: A

Question 33: If the equation x² + 5x + k = 0 has real and distinct roots, then ____

(A) k = 6 (B) k < 6.25 (C) k > 6 (D) k > 25

Answer: B