Bravais Lattice

Bravais Lattice refers to the 14 different 3-dimensional configurations into which atoms can be arranged in crystals. The smallest group of symmetrically aligned atoms which can be repeated in an array to make up the entire crystal is called a unit cell.

There are several ways to describe a lattice. The most fundamental description is known as the Bravais lattice. In words, a Bravais lattice is an array of discrete points with an arrangement and orientation that look exactly the same from any of the discrete points, that is the lattice points are indistinguishable from one another.

Thus, a Bravais lattice can refer to one of the 14 different types of unit cells that a crystal structure can be made up of. These lattices are named after the French physicist Auguste Bravais.

Table of Contents

• 14 Types of Bravais Lattices
• Frequently Asked Questions – FAQs

14 Types of Bravais Lattices

Out of 14 types of Bravais lattices some 7 types of Bravais lattices in three-dimensional space are listed in this subsection. Note that the letters a, b, and c have been used to denote the dimensions of the unit cells whereas the letters 𝛂, 𝞫, and 𝝲 denote the corresponding angles in the unit cells.

1. Cubic Systems

In Bravais lattices with cubic systems, the following relationships can be observed.

a = b = c

𝛂 = 𝞫 = 𝝲 = 90^o

The 3 possible types of cubic cells have been illustrated below.

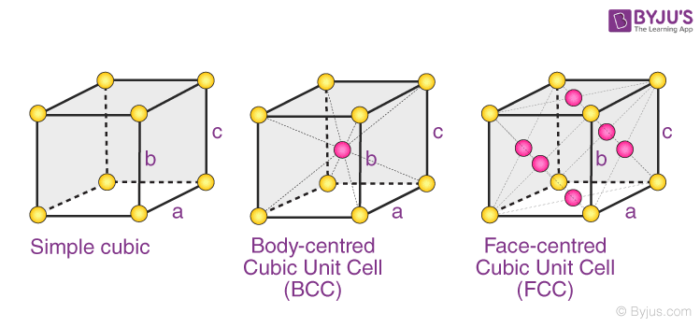
These three possible cubic Bravais lattices are –

• Primitive (or Simple) Cubic Cell (P)
• Body-Centered Cubic Cell (I)
• Face-Centered Cubic Cell (F)

Examples: Polonium has a simple cubic structure, iron has a body-centered cubic structure, and copper has a face-centered cubic structure.

2. Orthorhombic Systems

The Bravais lattices with orthorhombic systems obey the following equations:

a ≠ b ≠ c

𝛂 = 𝞫 = 𝝲 = 90^o

The four types of orthorhombic systems (simple, base centered, face-centered, and body-centered orthorhombic cells) are illustrated below.

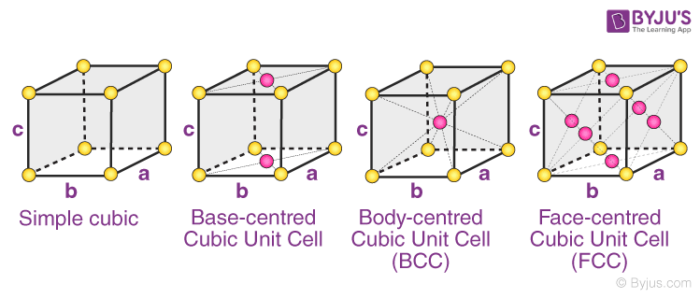
Examples of Orthorhombic Systems:

• Rhombic Sulphur has a simple orthorhombic structure
• Magnesium sulfate heptahydrate (MgSO₄.7H₂O) is made up of a base centred orthorhombic structure.
• Potassium Nitrate has a structure which is body-centered orthorhombic.
• An example of a substance with a face-centered orthorhombic structure is barium sulfate.

3. Tetragonal Systems

In tetragonal Bravais lattices, the following relations are observed:

a = b ≠ c

𝛂 = 𝞫 = 𝝲 = 90^o

The two types of tetragonal systems are simple tetragonal cells and body-centered tetragonal cells, as illustrated below.

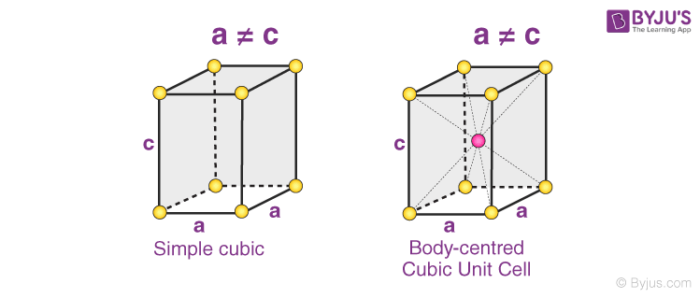
Examples of tetragonal Bravais lattices are – stannic oxide (simple tetragonal) and titanium dioxide (body-centered tetragonal)

4. Monoclinic Systems

Bravais lattices having monoclinic systems obey the following relations:

a ≠ b ≠ c

𝞫 = 𝝲 = 90^o and 𝛂 ≠ 90^o

The two possible types of monoclinic systems are primitive and base centered monoclinic cells, as illustrated below.

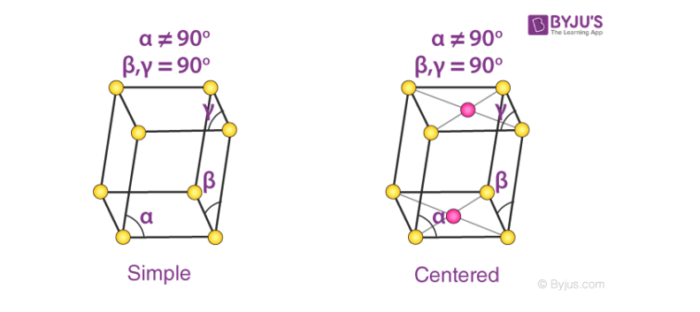
Cubic cells are – Monoclinic sulphur (simple monoclinic) and sodium sulfate decahydrate (base centered monoclinic)

5. Triclinic System

There exists only one type of triclinic Bravais lattice, which is a primitive cell. It obeys the following relationship.

a ≠ b ≠ c

𝛂 ≠ 𝞫 ≠ 𝝲 ≠ 90^o

An illustration of a simple triclinic cell is given below.

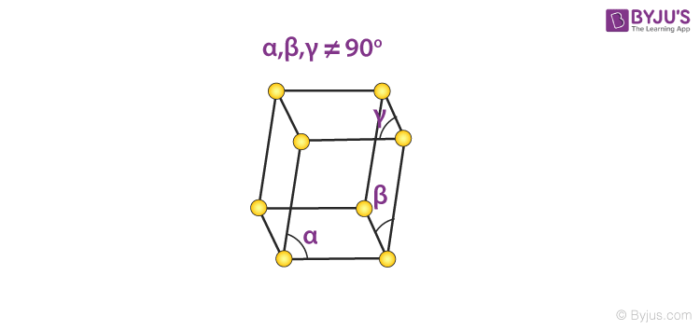
Such unit cells are found in the structure of potassium dichromate (Chemical formula K₂Cr₂O₇).

6. Rhombohedral System

Only the primitive unit cell for a rhombohedral system exists. Its cell relation is given by:

a = b = c

𝛂 = 𝞫 = 𝝲 ≠ 90^o

An illustration of the primitive rhombohedral cell is provided below.

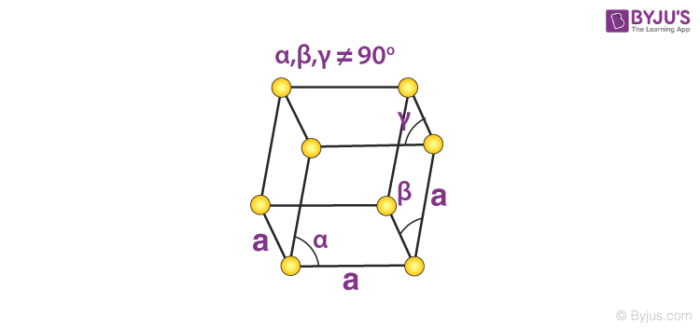
Calcite and sodium nitrate are made up of simple rhombohedral unit cells.

7. Hexagonal System

The only type of hexagonal Bravais lattice is the simple hexagonal cell. It has the following relations between cell sides and angles.

a = b ≠ c

𝛂 = 𝞫 = 90^o and 𝝲 = 120^o

An illustration of a simple hexagonal cell is provided below.

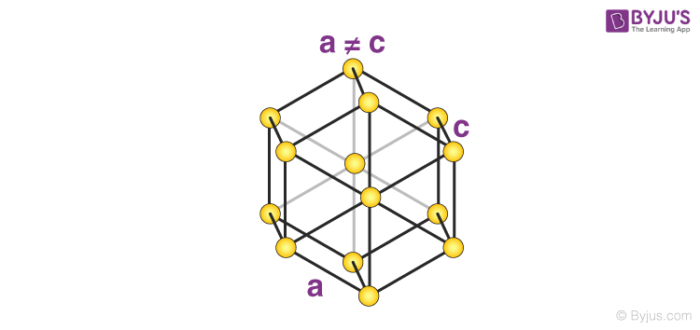
Zinc oxide and beryllium oxide are made up of simple hexagonal unit cells.

Thus, it can be noted that all 14 possible Bravais lattices differ in their cell length and angle relationships. It is important to keep in mind that the Bravais lattice is not always the same as the crystal lattice.