Calculating Equilibrium Concentrations

In a chemical reaction, when both the reactants and the products are in a concentration which does not change with time any more, it is said to be in a state of chemical equilibrium. In this state, the rate of forward reaction is same as the rate of backward reaction. For a reaction, if you know the initial concentrations of the substances, you can calculate the equilibrium concentration. Let us see how we do it with the help of an example.

Steps to Calculate Equilibrium Concentration

Problem Statement: At 300K, 6.00 moles of PCl₅ kept in 1 L closed reaction vessel was allowed to attain equilibrium. You are required to find the composition of the mixture at equilibrium. Given that K_c for the reaction is 1.

• Step1: Write the balanced equation for the reaction for which the concentration is to be calculated.

PCl₅⇌ PCl₃ + Cl₂

• Step 2: Convert the given concentrations into Molarity. Here the amount of PCl₅ before the reaction is 6 moles and the volume of the reaction vessel is 1 L. Therefore, the concentration of PCl₅ is 6/1 moles/litre = 6 M.

• Step 3: Make a note of the initial concentration and the change in concentration for each substance on undergoing equilibrium. Change in concentration is calculated by taking x as the concentration of one of the reactants and then finding out the concentrations of other substances in terms of x.

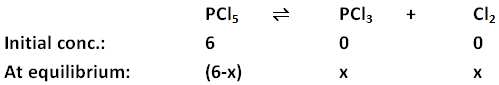
• Step 4: Using the K_c provided in the problem statement, fill in the values of the equilibrium concentrations in the equation. Note: While writing concentrations at equilibrium in the equation below, only those substances are taken into consideration whose concentrations change considerably. 

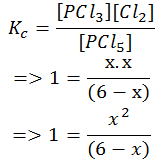
• Step 5: Solve for x. Since the concentration value cannot be negative, we take up the positive value of x. In other words, the value of x that makes chemical sense is taken.
  x²+ x -6 = 0
  The equation gives x = 2 or x = -3.

• Step 6: Calculate the values of equilibrium concentration for each substance using the value of x.
  Thus, we have
  [PCl₅] = 6 – x = 6 – 2 = 4 M
  [PCl₃] = [Cl₂] = x = 2 M

Recommended Video

Introduction to Chemical Equilibrium

To learn more about equilibrium concentration calculations, Gibbs free energy and to watch vibrant video lessons on the same, download BYJU’S The Learning App.