Energy in Simple Harmonic Motion

Energy is a quantitative property of the matter, which is the key factor for performing the work. Energy is defined as the ability to do work. Energyis the fundamental unit for many types of motions. Energy, depending on the intensity, can lead to deformations too. According to the laws of conservation of energy, it is stated that “energy cannot be created or destroyed, although it can be changed from one form to another”. The international system of units of measurement of energy is Joule.

There are many types of energy. Many objects store energy in order to perform work. Batteries store chemical and potential energy. Biomass and petroleum store chemical energy. Mechanical energy is stored in the stretched rubber bands. Solar energy is an example of radiant energy. Rock on the top of a hill stores gravitational potential energy. Lightning stores electrical energy.

Examples: Gasoline undergoes combustion reaction inside the car’s engine in order to operate the car. Here chemical Energy is converted into mechanical energy. Solar cells convert light energy into electrical energy.

We can observe in the above examples that one form of energy is converted into another form and is not wasted. Energy is stored for a purpose in various bodies, objects and devices.

Through the following ways, energy can be transferred:

  • By Radiation – By light waves or sound waves
  • Mechanically – By the action of force
  • Electrically – By the flow of electric current
  • By Heating – By conduction, convection, or radiation

Oscillations and Simple Harmonic Motion

Oscillations are repetitive variations that are periodic. Oscillations are measured about a point of equilibrium, also known as central value or between two or more different states. Repeating variations of any quantity or measure about its equilibrium value in time is defined as oscillation. Oscillations also occur in dynamic systems or, more accurately, in every field of science.

Example: The movement of a simple pendulum in a clock.

Simple Harmonic Motion or SHM is defined as a motion in which the restoring force is directly proportional to the displacement of the body from its mean position. SHM is a special case of oscillation in which motion takes place along a straight line between the two extreme points. A restoring force is seen directed towards the mean position or towards the equilibrium position in SHM. The mean position in simple harmonic motion is a stable equilibrium.

Note: All the SHM are oscillatory and periodic.

Every oscillatory motion is not a simple harmonic motion.

Let us know the energy in simple harmonic motion.

Read More: Simple Harmonic Motion

Energy in Simple Harmonic Motion

We can note there involves a continuous interchange of potential and kinetic energy in a simple harmonic motion. The system that performs simple harmonic motion is called the harmonic oscillator.

Case 1: The potential energy is zero, and the kinetic energy is maximum at the equilibrium point where zero displacement takes place.

Case 2: The potential energy is maximum, and the kinetic energy is zero, at a maximum displacement point from the equilibrium point.

Case 3: The motion of the oscillating body has different values of potential and kinetic energy at other points.

Consider a particle of mass m, executing linear simple harmonic motion with angular frequency(ω) and amplitude(A).

\(\begin{array}{l} \textup{The displacement}(\vec{x}),\textup{ velocity}(\vec{v}), \textup{ and acceleration} (\vec{a}) \textup{ at any time t are given by } \end{array} \)
\(\begin{array}{l}x = A sin (\omega t + \phi)\end{array} \)
\(\begin{array}{l}v = A\omega \cos \left( \omega t+\phi \right)=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}\end{array} \)
\(\begin{array}{l}a = -{{\omega }^{2}}A\sin \left( \omega t+\phi \right)=-{{\omega }^{2}}x\end{array} \)
\(\begin{array}{l} \textup{The restoring force } ( \vec{F}) \textup{ acting on the particle is given by} \end{array} \)

F = -kx

Where k = mω2.

Read More: Frequency, Time Period and Angular Frequency

Kinetic Energy of a Particle in Simple Harmonic Motion

\(\begin{array}{l}\textup{Kinetic Energy} = \frac{1}{2}m{{v}^{2}} \,\,\, \left[ Since, \;{{v}^{2}}={{A}^{2}}{{\omega }^{2}}{{\cos }^{2}}\left( \omega t+\phi \right) \right]\end{array} \)
\(\begin{array}{l} = \frac{1}{2}m{{\omega }^{2}}{{A}^{2}}{{\cos }^{2}}\left( \omega t+\phi \right)\end{array} \)
\(\begin{array}{l} = \frac{1}{2}m{{\omega }^{2}}\left( {{A}^{2}}-{{x}^{2}} \right)\end{array} \)
\(\begin{array}{l} \therefore \textup{Kinetic Energy} = \frac{1}{2}m{{\omega }^{2}}{{A}^{2}}{{\cos }^{2}}\left( \omega t+\phi \right)=\frac{1}{2}m{{\omega }^{2}}\left( {{A}^{2}}-{{x}^{2}} \right)\end{array} \)

Potential Energy of Simple Harmonic Motion

Work done by the restoring force while displacing the particle from the mean position (x = 0) to x = x:

The work done by restoring force when the particle has been displaced from the position x to x + dx is given by

dw = F dx = -kx dx

\(\begin{array}{l}w = \int{dw}=\int\limits_{0}^{x}{-kxdx=\frac{-k{{x}^{2}}}{2}}\end{array} \)
\(\begin{array}{l}= -\frac{m{{\omega }^{2}}{{x}^{2}}}{2}\end{array} \)
\(\begin{array}{l}\left[ \,k=m{{\omega }^{2}} \right]\end{array} \)
\(\begin{array}{l}= -\frac{m{{\omega }^{2}}}{2}{{A}^{2}}{{\sin }^{2}}\left( \omega t+\phi \right)\end{array} \)

Potential Energy = -(work done by restoring force)

\(\begin{array}{l}\textup{Potential Energy} = \frac{m{{\omega }^{2}}{{x}^{2}}}{2}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}{{\sin }^{2}}\left( \omega t+\phi \right)\end{array} \)

Read More: Types of Motion

Total Mechanical Energy of the Particle Executing Simple Harmonic Motion

The total energy of the system of a block and a spring is equal to the sum of the potential energy stored in the spring plus the kinetic energy of the block and is proportional to the square of the amplitude.

\(\begin{array}{l}\frac{1}{2}m{{\omega}^{2}}\left({{A}^{2}}-{{x}^{2}}\right)+\frac{1}{2}m{{\omega}^{2}}{{x}^{2}}\end{array} \)
\(\begin{array}{l}E = \frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\end{array} \)

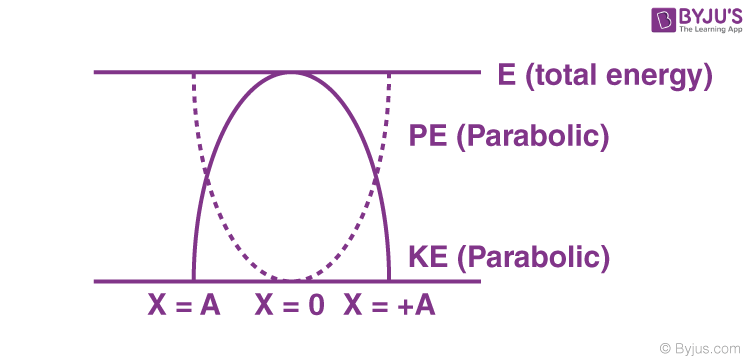
Hence, the total energy of the particle in SHM is constant and it is independent of the instantaneous displacement. Relationship between potential energy, kinetic energy, and time in Simple Harmonic Motion at t = 0, when x = ±A.

Simple harmonic motion image 8

Variation of kinetic energy and potential energy in SHM with displacement:

Simple harmonic motion image 9

Related Links

Relative Motion

Protection Against Earthquake

Lenz Law

Radioactivity – Alpha Decay

Frequently Asked Questions on Simple Harmonic Motion

Q1

1. What is a simple harmonic motion?

Simple harmonic motion is a periodic motion in which the particle acceleration is directly proportional to its displacement and is directed towards the mean position.

Q2

2. Give an example of periodic motion.

Motion of a pendulum.

Q3

3. A motion that repeats itself after an equal interval of time is known as

Periodic motion.

Q4

4. State the law of conservation of energy.

It states that “energy cannot be created or destroyed, although it can be changed from one form to another”.

Q5

5. Give an example for simple harmonic motion.

Oscillation of a simple pendulum.

Stay tuned with BYJU’S for more such interesting articles on physics, chemistry and maths in an engaging way with video explanations.

Test your Knowledge on Energy In Simple Harmonic Motion
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!

Select the correct answer and click on the "Finish" button
Check your score and explanations at the end of the quiz

Congrats!

Visit BYJU'S for all Physics related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted
PHYSICS Related Links
Examples Of Electromagnetic Waves Physics Numericals For Class 9 Motion With Answers
Difference Between Ac And Dc Generator Source Of Energy
Atomic Radius Definition State The Law Of Conservation Of Momentum
Insulator Definition Physics What Is Rectilinear Motion
Non Contact Force Examples Destructive Interference

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*