AP Board Class 9 Maths Chapter 7 Triangles

The topic of triangles in Maths is usually studied in many classes. However, as students progress from a primary to secondary to higher education, the topic gets more advanced and students have to study it in more depth along with many other related terms. As such, in Class 9 Maths of Andhra Pradesh board, students are introduced to properties of triangles and other complex concepts like;

• Congruence of Triangles.
• Properties of a Triangle
• Different Congruence rules.
• Inequalities in a Triangle.

This AP Board Class 9 Maths Chapter 7 Triangles are the perfect resource to revise the concepts of the subject thoroughly. Students can refer to this before the exams to get an idea about the topics covered.

Triangle

A triangle is a plane figure having three straight sides and usually three angles. Some of the different types of triangles are a right triangle, equilateral triangle, isosceles triangle, scalene triangle, acute triangle and obtuse triangle.

Properties of A Triangle

1. Vertex: The corner part on a triangle is known as a vertex.
2. Base: It is usually drawn at the bottom, but can be anyone among the three sides.
3. Altitude: The perpendicular from the base to the opposite vertex is the altitude of a triangle.
4. Interior angles: The angles present on the inside of a triangle.
5. Exterior angles: The angles between a side of a triangle and the extension of an adjacent side.

Congruence of Triangles

Two triangles are said to be congruent if the sides of one triangle are equal to the sides of another triangle and the corresponding angles are equal in the two triangles.

Students can view some of the chapter questions along with their solutions to know more about the concept.

Question 1: Mid-points of equal sides AB and AC of “ABC are given as E and F in the figure. Prove that BF = CE.

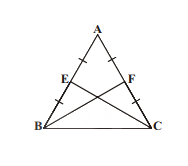
Solution: In [latex]\Delta ABF and \Delta ACE[/latex]

Given AB = AC

AF = AE (Halves of equal sides)

Therefore, BF = CE (CPCT)

Know more about AP Board and access various study materials, including syllabus, exam timetable, etc. at BYJU’s.

Also Read;