Andhra Pradesh SSC Board Question Paper for Class 10th Maths Paper 1 2018 In PDF

AP SSC or 10th Class Question Paper Mathematics Paper 1 English Medium 2018 with Solutions – Free Download

Andhra Pradesh SSC (Class 10) Maths 2018 question paper 1 with solutions are available here in a downloadable pdf format and also in the text so that the students can easily access them. Along with the solutions, they can also get the Maths question paper 1 2018 Class 10 SSC for reference. Students are able to access all the Andhra Pradesh board previous year maths question papers here. AP 10th Class Mathematics Question Paper 2018 Paper 1 can be downloaded easily and students can use them and verify the answers provided by BYJU’S. Solving 2018 Maths question paper 1 for Class 10 will help the students to predict what type of questions will appear in the exam.

Download SSC 2018 Question Paper Maths Paper 1

Download SSC 2018 Question Paper Maths Paper 1 With Solutions

Andhra Pradesh SSC Class 10th Maths Question Paper 1 With Solution 2018

QUESTION PAPER CODE 15E(A)

SECTION – I

(4 * 1 = 4)

Question 1: Find the HCF of 60 and 100 by using Euclid’s division lemma.

Solution:

Using Euclid’s division lemma –

100 = (60 × 1) + 40

60 = (40 × 1) + 20

40 = (20 × 2) + 0

The remainder is 0.

The HCF of 60 and 100 is 20.

Question 2: Write A = {3, 9, 27, 81} in set builder form.

Solution:

A = {3 , 9 , 27 , 81}

Set builder form

A = {x : x = 3ⁿ, n belongs to N & n < 5}

Question 3: Find the value of k for which the pair of equations 2x + ky + 3 = 0, 4x + 6y – 5 = 0 represent parallel lines.

Solution:

On comparing the given equations,

2x – ky + 3 = 0 ,

4x + 6y – 5 = 0 with

a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0

a₁ = 2 , b₁ = -k , c₁ = 3 ;

a₂ = 4 , b₂ = 6 , c₂ = -5 ;

a₁ / a₂ = b₁ / b₂ ≠ c₁ / c₂

a₁ / a₂ = b₁ / b₂

2 / 4 = (-k) / 6

(2 × -6) / 4 = k

k = -3 or 18 / 5

Question 4: Find the volume of the right circular cone with radius 3cm and height 14cm.

Solution:

Given the radius of the cone is 3cm and height is 14cm.

The volume of the cone = (⅓) πr²h

= (1 / 3) × (22 / 7) × 3 × 3 × 14

= 22 × 3 × 2

= 132cm³

SECTION – II

(5 * 2 = 10)

Question 5: Find the zeroes of the polynomial x² – 3 and verify the relationship between the zeroes and coefficients.

Solution:

x² – 3 = 0

x² = 3

x = ±√3

The zeroes of the given polynomial are √3 and -√3.

Relationship between the zeroes and coefficients

Sum of zeroes = √3 + (-√3) = √3 – √3 = 0 = coefficient of -x / coefficient of x²

Product of zeroes = (√3) (-√3) = -(√3)² = -3 / 1 = constant / coefficient of x²

Question 6: How many three-digit numbers are divisible by 3?

Solution:

The three-digit natural numbers start from 100 and end with 999.

The first three-digit number which is divisible by 3 is 102.

The last three-digit number which is divisible by 3 is 999.

The number of three-digit numbers divisible by 3

= 999 / 3 – (102 / 3) + 1

= 333 − 34 + 1

= 300

Question 7: A solid iron rod has a cylindrical shape. Its height is 11cm and base diameter is 7cm. Then find the total volume of 50 rods.

Solution:

The height of the cylinder is 11cm.

The diameter of the cylinder is 7cm.

The volume of cylinder = πr²h

= (22 / 7) * (7 / 2) * (7 / 2) * 11

= (121) * (7 / 2)

= 423.5

The volume of 50 such rods

= 50 × 423.5

= 21175 cm²

Question 8: Find the roots of x + (6 / x) = 7, x ≠ 0.

Solution:

x + (6 / x) = 7

x² – 7x + 6 = 0

x² – 6x – x + 6 = 0

x (x – 6) – 1 (x – 6) = 0

x = 1, 6

Question 9: Length of a rectangle is 2 units greater than its breadth. If the area of the rectangle is 120 square units, then find its length.

Solution:

Breadth = x

Length = x + 2

Area = 120 square units

x (x + 2) = 120

x² + 2x = 120

x² + 2x – 120 = 0

(x + 12)(x – 10) = 0

x = (-12), (10)

The value of x can’t be negative as it is the breadth of a rectangle.

x = 10

Breadth = 10

Length = x + 2 = 10 + 2 = 12

SECTION – III

(4 * 4 = 16)

Question 10:

[a] Hari went to a bank to withdraw Rs. 2000. He asked the cashier to give the cash in Rs. 50 and Rs. 100 separately. He got 25 notes in all. Can you tell how many notes, each of Rs. 50 and Rs. 100 he received?

OR

[b] How many spherical balls can be made out of a solid cube of lead, whose edges measure 66 cm and each ball being 3cm in radius?

Solution:

Let the number of Rs. 100 notes are ‘y’.

Total notes = 25

⇒ x + y = 25

⇒ x = 25 – y

Total amount only in Rs. 50 notes = 50x

Total amount only in Rs. 100 notes = 100y

Total amount = 2000

⇒ 50x + 100y = 2000

⇒ 50(25 – y) + 100y = 2000

⇒ 50* 25 – 50y + 100y = 2000

⇒ 1250 + 50 y = 2000

⇒ 50y = 2000 – 1250 = 750

⇒ y = 750 / 50 = 15

x = 25 – 15 = 10

The number of Rs. 50 notes = 10

The number of Rs. 100 notes = 15

Length of the edge of cube = 66 cm

The volume of each ball is given by V = (4 / 3) πr³

= (4 / 3) * (22 / 7) * (3³)

= 113.14 cm³

The volume of a cube is given by a³ = 66³ = 287496

So, the number of spherical balls is given by

= volume of the cube / volume of the ball

= 287496 / 113.14

= 2541

Hence, there are 2541 spherical balls that can be made.

Question 11:

[a] Show that √3 is irrational.

OR

[b] If A = {x : x is a natural number }

B = {x : x is an even number}

C = {x : x is an odd number}

D = {x : x is a prime number}

Then find A ∪ B, A ∩ C, B ∩ C and B ∩ D. What do you notice?

Solution:

Then, there exist positive integers a and b such that √3 = a / b, where a and b are coprime, their HCF is 1.

√3 = a / b

⇒ 3 = a² / b²

⇒ 3b² = a²

⇒ 3 divided a²

⇒ 3 divides a —- (1)

⇒ a = 3c for some integer c

⇒ a² = 9c²

⇒ 3b² = 9c²

⇒ b² = 3c²

⇒ 3 divides b²

⇒ 3 divides b —- (2)

From (i) and (ii), it is observed that a and b have at least 3 as a common factor. But, this contradicts the fact that a and b are co-prime. This means that our assumption is not correct.

Hence, √3 is an irrational number.

A ∩ C = {all odd numbers}

B ∩ C = { }

B ∩ D = {2}

Question 12:

[a] The sum of the reciprocals of Rehman’s age, (in years) 3 years ago and 5 years from now is 1 / 3. Find the present age.

OR

[b] If the sum of the first 7 terms and 15 terms of an AP are 98 and 390, respectively. Find the sum of the first 10 terms.

Solution:

Rehman’s 3 years ago age will be x – 3. ———– (2)

Rehman’s 5 years ago age will be x + 5. ———- (3)

Given, the sum of reciprocals of (1), (2), (3) will be 1 / 3.

6x + 6 = x² + 2x – 15

x² + 2x – 15 – 6x – 6 = 0

x² – 4x – 21 = 0

(x – 7) (x – 3) = 0

x = 7 or x = -3.

The value of x cannot be negative.

So, the present age of Rehman is 7 years.

Sum = (n / 2) (2a + [n – 1]d)

98 = (7 / 2) (2a + 6d)

28 = 2a + 6d

14 = a + 3d —- (1)

390 = (15 / 2) (2a + [15 – 1] d)

52 = 2a + 14d

26 = a + 7d —- (2)

On solving the equations (1) and (2),

a = 5 and d = 3

Sum to 10 terms

= [10 / 2] * (2 * 5 + (10 – 1) * 3

= 5 (10 + 27)

= 37 * 5

= 185

Question 13:

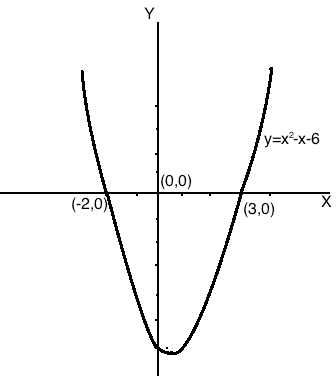
[a] Solve the quadratic polynomial p(x) = x² – x – 6 by graphical method.

OR

[b] The perimeter of a rectangular plot is 32m. If the length is increased by 2m and the breadth is decreased by 1m, then the area of the plot remains the same. Find the length and breadth of the plot.

Solution:

y intercept at x = 0

y = 0 – 0 – 6 = – 6

x intercept at y = 0

x² – x – 6 = 0

x² – 3x + 2x – 6 = 0

x (x – 3) + 2 (x – 3) = 0

(x – 3) (x + 2) = 0

x = 3, -2

Perimeter = 32 m ( given )

2(l + b) = 32

l + b = 16 — ( 1 )

If length is increased by 2 m and the breadth is decreased by 1 m, the area of the plot remains the same .

( l + 2 ) ( b – 1 ) = lb

lb – l + 2b – 2 = lb

– l + 2b = 2 — ( 2 )

Add equations ( 1 ) and ( 2 ),

3b = 18

b = 18 /3

b = 6

Put b = 6 in equation ( 1 ),

l + b = 16

l + 6 = 16

l = 10

Therefore, length of the rectangle plot = l = 10m and breadth = b = 6 m.

SECTION – IV

(20 * 0.5 = 10)

Question 14: Which of the following is a terminating decimal?

(A) 10 / 81 (B) 41 / 75 (C) 8 / 125 (D) 3 /14

Answer: C

Question 15: The value of log₂ 32 is ____

(A) 2 (B) 32 (C) I / 5 (D) 5

Answer: D

Question 16: If 3 is one of the zeroes of p(x) = x² + kx – 9, the the value of k is

(A) 0 (B) 1 (C) 2 (D) 3

Answer: A

Question 17: The pair of equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, are consistent, then

(A) a₁ / a₂ ≄ b₁ / b₂

(B) a₁ / a₂ = b₁ / b₂ ≄ c₁ / c₂

(C) a₁ / a₂ = b₁ / b₂ = c₁ / c₂

(D) A and C

Answer: D

Question 18: If ɑ, β, Ɣ are the zeroes of the cubic polynomial ax³ + bx² + cx + d and (ɑ ≄ 0), then ɑβƔ is

(A) d / a (B) -d / a (C) -b / a (D) c / a

Answer: B

Question 19: Which term of an AP 18, 15, 12 … equals to 0?

(A) 4 (B) 5 (C) 6 (D) 7

Answer: D

Question 20: If A ⊂ B, n(A) = 4, n(B) = 6, then n(A ∪ B) = ___

(A) 10 (B) 6 (C) 4 (D) 2

Answer: C

Question 21: If k, 2k + 1, 2k + 3 are three consecutive terms in AP, then the value of k is

(A) 1 (B) 0 (C) 2 (D) 3

Answer: A

Question 22: A quadratic polynomial, whose zeroes are √2 and – √2 is

(A) x² – 4 (B) x² + 4 (C) x² – 2 (D) x² + 2

Answer: C

Question 23: If a_n = n / (n + 1), then a₂₀₁₇ =

(A) 2017 / 2016 (B) 2017 / 2018 (C) 2017 / 2019 (D) 2018 / 2017

Answer: B

Question 24: A cylinder and cone have bases of equal radii and are of equal heights, then their volumes are in the ratio

(A) 1:1 (B) 1:3 (C) 3:1 (D) 1:9

Answer: C

Question 25: Total surface area of a solid hemisphere of radius 7cm is _____ cm².

(A) 21𝛑 (B) 49 𝛑 (C) 147𝛑 (D) 98𝛑

Answer: C

Question 26: A quadratic equation ax² + bx + c = 0 has 2 distinct real roots, if

(A) b² – 4ac > 0 (B) b² – 4ac < 0 (C) b² – 4ac = 0 (D) None of these

Answer: A

Question 27: The degree of the polynomial 5x⁷ – 6x⁵ + 7x – 4 is

(A) 5 (B) 6 (C) 7 (D) 4

Answer: C

Question 28: The n^th term of a progression a, ar, ar², is

(A) ar (B) ar² (C) a + (n – 1)r (D) ar^n-1

Answer: D

Question 29: Which of the following equations has the solution of (1, -1)?

(A) 3x – 2y = 6 (B) 3x + 2y = 6 (C) 3x – 2y = 5 (D) 3x + 2y = 5

Answer: C

Question 30: If A = {x : x is a letter in the word EXAMINATION, then its roster form is

(A) A = {e, x, m, i, n, a, t, o, s}

(B) A = {e, x, m, i, n, a, t, o}

(C) A = {e, x, m, a, i, n, t, s}

(D) A = {e, x, m, i, n, t, o}

Answer: B

Question 31: The following Venn diagram indicates

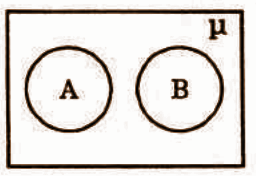
(A) A ⊂ B (B) B ⊂ A (C) A, B are disjoint sets (D) A = B

Answer: C

Question 32: The discriminant of the quadratic equation px² + qx + r = 0 is

(A) p² – 4qr (B) q² – 4pr (C) q² + 4pr (D) r² – 4pq

Answer: B

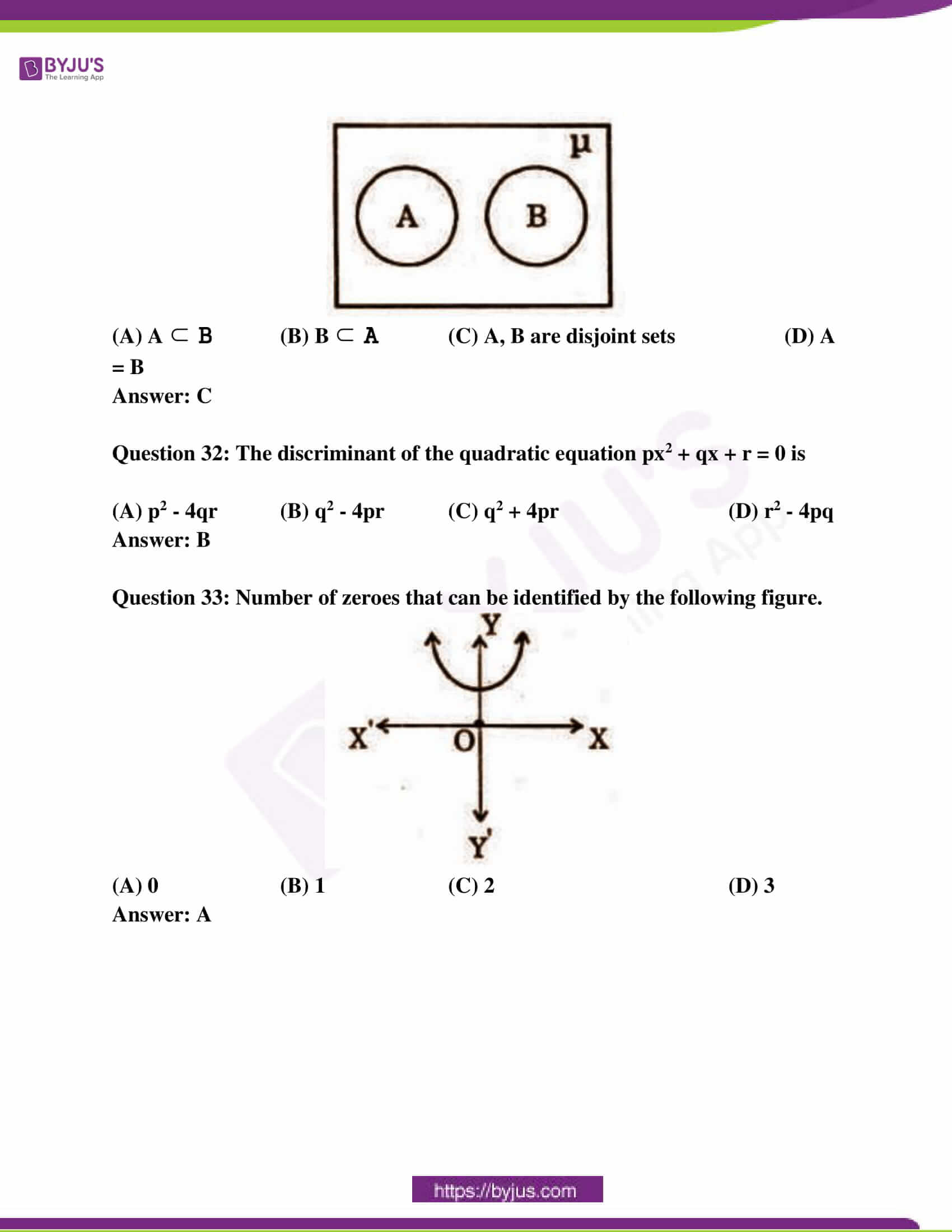
Question 33: Number of zeroes that can be identified by the following figure.

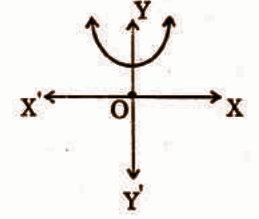
(A) 0 (B) 1 (C) 2 (D) 3

Answer: A