IIT Kanpur will conduct the GATE Mathematics (MA) 2023 Exam. GATE 2023 Mathematics Paper had a total of 65 questions. Of these total questions, 55 questions were on Mathematics, and 10 questions were on the General Aptitude section. The candidates who opt for Mathematics as their first paper in GATE Exam can also appear for Computer Science and Information Technology (CS), Geomatics Engineering (GE), Physics (PH), or Statistics (ST) as their second choice of paper in GATE 2023.
Get all the necessary information like syllabus, exam pattern, new changes introduced in GATE, important books, preparation tips, previous years’ question papers, cut off, and latest news related to GATE Mathematics Exam here. We have also provided direct links to the Answer Key and Question Papers.
Table of Contents:
- GATE Maths Latest News
- GATE Maths Overview
- GATE Maths Related Study Resources
- Books for GATE Maths
- GATE Maths Important Dates 2023
- GATE Maths (MA) Exam Pattern
- GATE Maths Paper Analysis 2022
- GATE Maths Results Analysis
- Frequently Asked Questions
GATE Maths Latest News
GATE 2023 Mathematics aspirants can now access the GATE Syllabus and GATE Exam Dates on the official website.
GATE Maths Overview
| Particulars | Details |
| Number of Questions in Paper | 65 |
| Number of Sections | Section 1 – General Aptitude, Section 2 – Mathematics and Computer Science Engineering |
| Topic-wise Weightage | General Aptitude – 15%
Mathematics – 85% |
| Pattern of Questions | Multiple Choice Question (MCQs) and Numerical Answer Type Questions (NATQs) |
| Duration of Exam | 3 Hours |
| Marking Scheme | Test paper has questions carrying 1 mark and 2 marks, and
⅓ and ⅔ negative mark for incorrect answers, respectively |
GATE Mathematics Related Study Resources
Books for GATE Maths
Some of the important books for GATE MA are listed below:
| Subject | Book Title | Author |
| Linear Algebra | Linear Algebra | Seymour Lipschutz, Marc Lipson |
| Linear Algebra and its Applications | Gilbert Strang | |
| Complex Analysis | Complex Analysis | Gamelin |
| Complex Analysis for Mathematics and Engineering | J. H. Mathews | |
| Foundations of Complex Analysis | S. Ponnusamy | |
| Real Analysis | Real Analysis | Royden H.L., Fitzpatrick P. M |
| Introduction to Real analysis | Donald R. Sherbert, Robert G. Bartle | |
| Elements of Real Analysis | Shanti Narayan, M D Raisinghania | |
| Ordinary Differential Equations | Ordinary Differential Equations | Purna Chandra Biswal |
| An Introduction to Ordinary Differential Equations | Earl A. Coddington | |
| Ordinary and Partial Differential Equations | M. D. Raisinghania | |
| Partial Differential Equations | Ordinary and Partial Differential Equations | M. D. Raisinghania |
| Elements of Partial Differential Equations | Ian N. Sneddon | |
| Introduction to Partial Differential Equations | Sankara Rao | |
| Algebra | Topics in Algebra | I. N. Herstein |
| Linear Algebra | Ian N. Sneddon, Seymour Lipschutz, Marc Lipson | |
| Functional Analysis | Functional Analysis | Rudin |
| Introductory Functional Analysis with Applications | Erwin Kreyszig | |
| Numerical Analysis | Numerical Analysis | Francis Scheid |
| Introductory Methods of Numerical Analysis | Sastry S. S. | |
| Numerical Methods – Principles, Analysis & Algorithms | Srimanta Pal | |
| Mechanics | Classical Mech | John Safko, Charles P. Poole Herbert Goldstein |
| Engineering Mechanics | S. S. Bhavikatti | |
| Topology | Topology | James R. Munkres |
| Introduction to Topology and Modern Analysis | S. S. Bhavikatti | |
| Probability and Statistics | Probability and Statistics | John J. Schiller |
| Introduction to Probability and Statistics for Engineers and Scientists | Sheldon M. Ross | |
| Probability, Random Variables and Stochastic Processes | S Pillai, Athanasios Papoulis | |
| Linear Programming | Linear Programming | G. Hadley, J.G Chakraborty &
P. R. Ghosh |
| Linear Programming and Network Flows | Mokhtar S. Bazaraa, John J. Jarvis, Hanif D. Sherali | |
| Calculus of Variation and Integral Equations | An Introduction to the Calculus of Variations | Pars |
| Calculus of Variations | I. M. Gelfand, Wendy Ed. Silverman | |
| Integral Transforms, Integral Equations, and Calculus of Variations | P. C. Bhakta |
GATE Maths Important Dates 2023
| Particulars | Dates |
| GATE online application processing | 30th August, 2022 |
| Closing of submission of application form | 30th September, 2022 |
| Last date of the extended period for online registration application (with late fees) | 7th October, 2022 |
| Modifications in GATE 2023 Application | 4th to 11th November, 2022 |
| Admit Card | 3rd January, 2023 |
| GATE 2023 examination | 4th, 5th, 11th and 12th February, 2023 |
| Announcement of result | 16th March, 2023 |
GATE Maths (MA) Exam Pattern
Let us take a look at the GATE Exam pattern for the 2022 exam for Maths:
| Feature | Description |
| Examination Mode | Online (Computer Based Test) |
| Duration of Exam | 3 Hours (180 Minutes) |
| Sectional Time Duration | None |
| Total Marks | 100 |
| Total Number of questions | 65 |
| Number of Subjects (Papers) | 29 |
| Number of Sections | It depends on the subjects.
2-3 (GA and Core Discipline or GA, Engineering Mathematics and Core Subject) |
| Type of Questions | Multiple Choice Questions (MCQs)
Multiple Select Questions (MSQs) Numerical Answer Type (NAT) Questions |
| Marking Scheme | 1 or 2 marks for each right answer |
| Negative Marking Scheme | For a wrong answer chosen in a MCQ, there will be negative marking.
For 1-mark MCQ, 1/3 mark will be deducted for a wrong answer. For 2-mark MCQ, 2/3 mark will be deducted for a wrong answer. NO negative marking for MSQ & NAT. |
Marking Scheme of GATE MA:
| Stream/ Course | Subject | Total No. of Questions | Marks Allotted |
| Mathematics | General Aptitude | 10 | 15 |
| Subjects | 55 | 85 | |
| Total | 65 | 100 |
GATE Mathematics Paper Analysis
IIT Kanpur will conduct the GATE Maths 2023 exam on February, 2023. You can find more details below:
| Particulars | Details |
| Question Type | MSQs
NATQs MCQs |
| Difficulty Level | Moderate |
| Highest weightage in the paper |
|
| General Aptitude | Moderate |
GATE Mathematics Results Analysis
GATE MA Topper Marks by Year
| Year | Subject | Marks |
| 2021 | Maths (MA) | 68.33 |
| 2020 | Maths (MA) | 61.0 |
| 2019 | Maths (MA) | 48.33 |
| 2018 | Maths (MA) | 49.67 |
| 2017 | Maths (MA) | 57.67 |
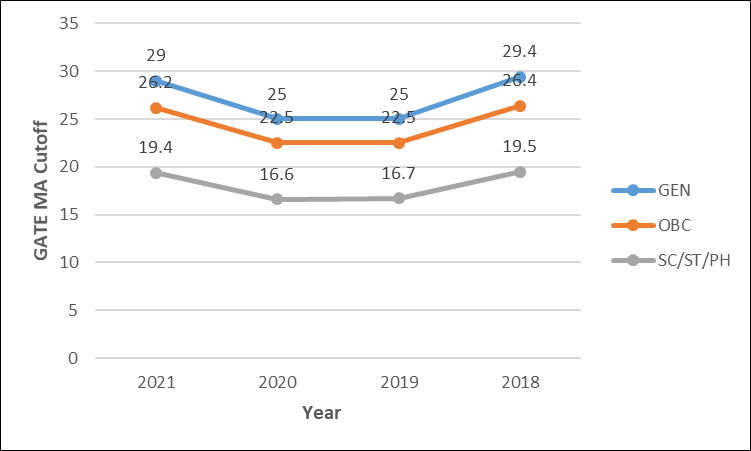
GATE MA Cutoff over Years
| Year | Subject | GEN | OBC | SC/ST/PH |
| 2021 | Maths (MA) | 29 | 26.2 | 19.4 |
| 2020 | Maths (MA) | 25 | 22.5 | 16.6 |
| 2019 | Maths (MA) | 25 | 22.5 | 16.7 |
| 2018 | Maths (MA) | 29.4 | 26.4 | 19.5 |
The graph shows the MA cutoff trend of the last 5 years:
Frequently Asked Questions
Who is eligible for GATE mathematics?
Anyone with a Master’s degree in any branch of Science/Mathematics/Statistics/Computer Applications or equivalent are eligible for GATE Mathematics.
How many attempts are there for GATE?
There is no limit for appearing GATE as per GATE 2023 notifications.
What is a good rank in GATE mathematics?
To get admission in top IITs, a rank below 200 is necessary.
Comments