ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations

ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations can be utilised by the students to comprehend the concepts and solve problems in an effective way. The solutions are clearly briefed in a step-by-step manner in order to help students understand easily. Further, these solutions are in accordance with the latest ICSE board guidelines. To learn more about these concepts, students can access the ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations PDF from the link provided below.

The main topics covered in this chapter are inequalities among real numbers, linear inequations and solving linear inequations in one variable using the two permissible rules. Students can start solving the problems on a regular basis so that their conceptual knowledge becomes stronger and their problem-solving skills are also improved, which is important from the examination perspective. Moreover, the ML Aggarwal Solutions can be used as a reference to answers and to learn the other methods of solving problems effortlessly.

ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations:

Download PDF

carouselExampleControls111

Previous



Next

Access ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations

Exercise 4

1. Solve the inequation, 3x – 11 < 3 where x ∈ {1, 2, 3, ……, 10}. Also, represent its solution on a number line.

Solution:

Given inequation, 3x – 11 < 3

3x < 3 + 11

3x < 14

⇒ x < 14/3

But, x ∈ {1, 2, 3,……, 10}

Hence, the solution set is {1, 2, 3, 4}.

Representing the solution on a number line:

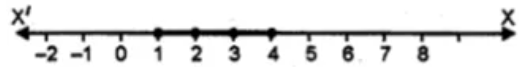
2. Solve 2(x – 3) < 1, x ∈ {1, 2, 3, …. 10}

Solution:

Given inequation, 2(x – 3) < 1

2x – 6 < 1

2x < 7

⇒ x < 7/2

But, x ∈ {1, 2, 3, …. 10}

Hence, the solution set is {1, 2, 3}

3. Solve 5 – 4x > 2 – 3x, x ∈ W. Also represent its solution on the number line.

Solution:

Given inequation, 5 – 4x > 2 – 3x

– 4x + 3x > 2 – 5

-x > -3

On multiplying both sides by -1, the inequality reverses

⇒ x < 3

Since, x ∈ W

The solution set is {0, 1, 2}

Representing the solution on a number line:

4. List the solution set of 30 – 4 (2x – 1) < 30, given that x is a positive integer.
Solution:

Given inequation, 30 – 4 (2x – 1) < 30

30 – 8x + 4 < 30

34 – 8x < 30

-8x < 30 – 34

-8x < -4 [On multiplying both sides by -1, the inequality reverses]

8x > 4

x > 4/8

⇒ x > 1/2

As x is a positive integer

The solution set is {1, 2, 3, … }

5. Solve: 2 (x – 2) < 3x – 2, x ∈ {– 3, – 2, – 1, 0, 1, 2, 3}.
Solution:

Given inequation, 2 (x – 2) < 3x – 2

2x – 4 < 3x – 2

2x – 3x < -2 + 4

-x < 2

⇒ x > -2

But, x ∈ {– 3, – 2, – 1, 0, 1, 2, 3}

Hence, the solution set is {– 1, 0, 1, 2, 3}.

6. If x is a negative integer, find the solution set of 2/3 + 1/3 (x + 1) > 0.
Solution:

Given inequation, 2/3 + 1/3 (x + 1) > 0.

2/3 + x/3 + 1/3 > 0

x/3 + 1 > 0

x/3 > -1

⇒ x > -3

As x is a negative integer

The solution set is {-1, -2}.

7. Solve x – 3 (2 + x) > 2 (3x – 1), x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}. Also represent its solution on the number line.
Solution:

Given inequation, x – 3 (2 + x) > 2 (3x – 1)

x – 6 – 3x > 6x – 2

-2x – 6 > 6x – 2

-6x – 2x > -2 + 6

-8x > 4

x < -4/8

⇒ x < -1/2

But, x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}

Hence, the solution set is {-3, -2, -1}

8. Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solve x – 3 < 2x – 1.

Solution:

Given inequation, x – 3 < 2x – 1

x – 2x < – 1 + 3

-x < 2

⇒ x > -2

But, x ∈ {1, 2, 3, 4, 5, 6, 7, 9}

Hence, the solution set is {1, 2, 3, 4, 5, 6, 7, 9}.

9. List the solution set of the inequation ½ + 8x > 5x – 3/2, x ∈ Z
Solution:

Given inequation, ½ + 8x > 5x – 3/2

8x – 5x > -3/2 – ½

3x > -4/2

⇒ x > -2/3

As x ∈ Z

The solution set is {0, 1, 2, 3, 4, 5, …}

10. List the solution set of (11 – 2x)/5 ≥ (9 – 3x)/8 + 3/4, x ∈ N

Solution:

Given inequation, (11 – 2x)/5 ≥ (9 – 3x)/8 + ¾

(11 – 2x)/5 ≥ (9 – 3x + 6)/8

8 (11 – 2x) ≥ 5 (15 – 3x)

88 – 16x ≥ 75 – 15x

15x – 16x ≥ 75 – 88

-x ≥ -13

⇒ x ≤ 13

As x ∈ N

Hence, the solution set is {1, 2, 3, 4, …, 13}.

11. Find the values of x, which satisfy the inequation : 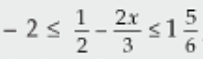 , x ∈ N. Graph the solution set on the number line.
Solution:

Given inequation,

-2 ≤ (3 – 4x)/ 6 ≤ 11/6

-12 ≤ 3 – 4x ≤ 11

-12 – 3 ≤ -4x ≤ 11 – 3

-15 ≤ -4x ≤ 8

-15/4 ≤ -x ≤ 8/4

⇒ 15/4 ≥ x ≥ -2

As x ∈ N,

The solution set is {1, 2, 3}.

Representing the solution on a number line:

12. If x ∈ W, find the solution set of 3/5 x – (2x – 1)/3 > 1. Also graph the solution set on the number line, if possible.
Solution:

Given inequation, 3/5 x – (2x – 1)/3 > 1

9/15 x – 5(2x – 1)/15 > 1 [Taking L.C.M]

9x – 5(2x – 1) > 15 [Multiplying by 15 on both sides]

9x – 10x + 5 > 15

-x > 15 – 5

-x > 10

⇒ x < -10

But, x ∈ W

Hence, the solution set is a null set.

Thus, it can’t be represented on number line.

13. Solve:

(i) x/2 + 5 ≤ x/3 + 6, where x is a positive odd integer.

(ii) (2x + 3)/3 ≥ (3x – 1)/4, where x is positive even integer.
Solution:

(i) Given inequation, x/2 + 5 ≤ x/3 + 6

(x + 10)/2 ≤ (x + 18)/3 [Taking L.C.M on both sides]

3 (x + 10) ≤ 2 (x + 18) [On cross-multiplying]

3x + 30 ≤ 2x + 36

3x – 2x ≤ 36 – 30

⇒ x ≤ 6

As x is a positive odd integer.

Hence, the solution set is {1, 3, 5}.

(ii) Given inequation, (2x + 3)/3 ≥ (3x – 1)/4

4 (2x + 3) ≥ 3 (3x – 1) [On cross-multiplying]

8x + 12 ≥ 9x – 3

-9x + 8x ≥ -12 – 3

-x ≥ -15

⇒ x ≤ 15

As x is a positive even integer.

Hence, the solution set is {2, 4, 6, 8, 10, 12, 14}.

14. Given that x ∈ I, solve the inequation and graph the solution on the number line:

3 ≥ (x – 4)/2 + x/3 ≥ 2

Solution:

Given inequation, 3 ≥ (x – 4)/2 + x/3 ≥ 2

Now, let’s take

3 ≥ (x – 4)/2 + x/3, we have

3 ≥ (3x – 12 + 2x)/6 [Taking L.C.M]

18 ≥ 5x – 12

30 ≥ 5x

⇒ x ≤ 6 …. (i)

Next,

(x – 4)/2 + x/3 ≥ 2

(3x – 12 + 2x)/6 ≥ 2

5x – 12 ≥ 12

5x ≥ 24

x ≥ 24/5 ⇒ x ≥ 4.8 … (ii)

Hence, from (i) and (ii) we have

Solution of x = {5, 6}

Representing the solution on a number line:

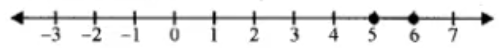
15. Solve: 1 ≥ 15 – 7x > 2x – 27, x ∈ N
Solution:

Given inequation, 1 ≥ 15 – 7x > 2x – 27,

So, we have

1 ≥ 15 – 7x and 15 – 7x > 2x – 27

7x ≥ 15 – 1 and -2x – 7x > -27 – 15

7x ≥ 14 and -9x > -42

x ≥ 2 and -x > -42/9

x ≥ 2 and x < 14/3

⇒ 2 ≤ x < 14/3

But as x ∈ N

The solution set is {2, 3, 4}.

16. If x ∈ Z, solve 2 + 4x < 2x – 5 ≤ 3x. Also represent its solution on the number line.
Solution

Given inequation, 2 + 4x < 2x – 5 ≤ 3x

So, we have

2 + 4x < 2x – 5 and 2x – 5 ≤ 3x

4x – 2x < -5 – 2 and 2x – 3x ≤ 5

2x < -7 and -x ≤ 5

x < -7/2 and x ≥ -5

⇒ -5 ≤ x < -7/2

As x ∈ Z

The solution set is {-5, -4}.

Representing the solution on a number line:

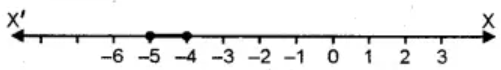
17. Solve: (4x – 10)/3 ≤ (5x – 7)/2, x ∈ R and represent the solution set on the number line.
Solution:

Given inequation, (4x – 10)/3 ≤ (5x – 7)/2

2 (4x – 10) ≤ 3 (5x – 7) [On cross-multiplying]

8x – 20 ≤ 15x – 21

8x – 15x ≤ -21 + 20

-7x ≤ -1

-x ≤ -1/7

x ≥ 1/7

As x ∈ R

Hence, the solution set is {x: x ∈ R, x ≥ 1/7}

Representing the solution on a number line:

18. Solve 3x/5 – (2x – 1)/3 > 1, x ∈ R and represent the solution set on the number line.
Solution:

Given inequation, 3x/5 – (2x – 1)/3 > 1

(9x – 10x + 5)/15 > 1 [Taking L.C.M]

-x + 5 > 15

-x > 15 – 5

-x > 10

x < -10

As x ∈ R

Hence, the solution set is {x: x ∈ R, x < -10}

Representing the solution on a number line:

19. Given that x ∈ R, solve the following inequation and graph the solution on the number line: -1 ≤ 3 + 4x < 23.

Solution:

Given inequation, -1 ≤ 3 + 4x < 23

-1 – 3 ≤ 4x < 23 – 3

-4 ≤ 4x < 20

-4/4 ≤ x < 20/4

-1 ≤ x < 5

Hence, the solution set is {-1 ≤ x < 5; x ∈ R}

Representing the solution on a number line:

20. Solve the following inequation and graph the solution on the number line.
 , x ∈ R
Solution:

Given inequation,

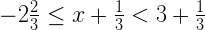
-8/3 ≤ (3x + 1)/3 < 10/3

-8 ≤ 3x + 1 < 10 [Multiplying by 3]

-8 – 1 ≤ 3x < 10 – 1

-9 ≤ 3x < 9

-3 ≤ x < 3 [Dividing by 5]

Thus, the solution set is {x: x ∈ R, -3 ≤ x < 3}

Representing the solution on a number line:

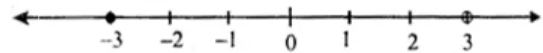
21. Solve the following inequation and represent the solution set on the number line:

Solution:

Given in equation,

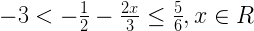
-3 < -(3 + 4x)/6 ≤ 5/6 [Taking L.C.M]

-18 < -3 – 4x ≤ 5 [Multiplying by 6]

-18 + 3 < -4x ≤ 5 + 3

-15 < -4x ≤ 8

-15/4 < -x ≤ 8/4

-2 ≤ x < 15/4

Hence, the solution set is {x : x ∈ R, -2 ≤ x < 15/4}

Representing the solution on a number line:

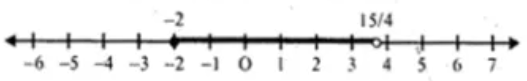
22. Solving the following inequation, write the solution set and represent it on the number line

-3(x – 7) ≥ 15 – 7x > 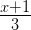, x ∈ R
Solution:

Given inequation, –3(x – 7) ≥ 15 – 7x >

–3x + 21 ≥ 15 – 7x > (x + 1)/3

So,

-3x + 21 ≥ 15 – 7x

7x – 3x ≥ 15 – 21

4x ≥ -6

x ≥ -6/4

x ≥ -3/2

And,

15 – 7x > (x + 1)/3

3(15 – 7x) > x + 1

45 – 21x > x + 1

-21x – x > 1 – 45

-22x > -44

-x > -44/22

x < 2

Hence, the solution set is {x : x ∈ R , -3/2 ≤ x < 2}

Representing the solution on a number line:

23. Solve the following inequation, write down the solution set and represent it on the real number line:

-2 + 10x ≤ 13x + 10 ≤ 24 + 10x, x ∈ Z

Solution:

Given inequation, -2 + 10x ≤ 13x + 10 ≤ 24 + 10x

So, we have

-2 + 10x ≤ 13x + 10 and 13x + 10 ≤ 24 + 10x

10x – 13x ≤ 10 + 2 and 13x – 10x ≤ 24 – 10

-3x ≤ 12 and 3x ≤ 14

x ≥ -12/3 and x ≤ 14/3

x ≥ -4 and x ≤ 14/3

So, -4 ≤ x ≤ 14/3

As x ∈ Z

Thus, the solution set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}

Representing the solution on a number line:

24. Solve the inequation 2x – 5 ≤ 5x + 4 < 11, where x ∈ I. Also represent the solution set on the number line.

Solution:

Given inequation, 2x – 5 ≤ 5x + 4 < 11

So, we have

2x – 5 ≤ 5x + 4 and 5x + 4 < 11

2x – 5x ≤ 4 + 5 and 5x < 11 – 4

-3x ≤ 9 and 5x < 7

-x ≤ 9/3 and x < 7/5

x ≥ -3 and x < 7/5

-3 ≤ x < 7/5

As x ∈ I

Thus, the solutions set is {-3, -2, -1, 0, 1}

Representing the solution on a number line:

25. If x ∈ I, A is the solution set of 2 (x – 1) < 3x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, find A ∩ B.
Solution:

Given inequations,

2 (x – 1) < 3x – 1 and 4x – 3 ≤ 8 + x for x ∈ I

Solving for both, we have

2x – 3x < 2 – 1 and 4x – x ≤ 8 + 3

-x < 1 and 3x ≤ 11

x > -1 and x ≤ 11/3

Hence,

Solution set A = {0, 1, 2, 3, …}

Solution set B = {3, 2, 1, 0, -1, … }

Thus, A ⋂ B = {0, 1, 2, 3}

26. If P is the solution set of -3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find
(i) P ∩ Q
(ii) Q – P.
Solution:

Given inequations,

-3x + 4 < 2x – 3 where x ∈ N and 4x – 5 < 12 where x ∈ W

So, solving

-3x + 4 < 2x – 3 where x ∈ N

-3x – 2x < -3 – 4

-5x < -7

x > 7/5

Hence, the solution set P is {2, 3, 4, 5, …}

And, solving

4x – 5 < 12 where x ∈ W

4x < 12 + 5

4x < 17

x < 17/4

Hence, the solution set Q is {0, 1, 2, 3, 4}

Therefore,

(i) P ∩ Q = {2, 3, 4}

(ii) Q – P = {0, 1}

27. A = {x : 11x – 5 > 7x + 3, x ∈ R} and

B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R}
Find the range of set A ∩ B and represent it on a number line
Solution:

Given, A = {x : 11x – 5 > 7x + 3, x ∈ R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R}

Solving for A,

11x – 5 > 7x + 3

11x – 7x > 3 + 5

4x > 8

x > 2

Hence, A = {x : x > 2, x ∈ R}

Next, solving for B

18x – 9 ≥ 15 + 12x

18x – 12x ≥ 15 + 9

6x ≥ 24

x ≥ 4

Hence, B = {x : x ≥ 4, x ∈ R}

Thus, A ∩ B = x ≥ 4

Representing the solution on a number line:

28. Given: P {x : 5 < 2x – 1 ≤ 11, x ∈ R}
Q {x : – 1 ≤ 3 + 4x < 23, x ∈ I} where
R = (real numbers), I = (integers)
Represent P and Q on number line. Write down the elements of P ∩ Q.
Solution:

Given, P {x : 5 < 2x – 1 ≤ 11, x ∈ R} and Q {x : – 1 ≤ 3 + 4x < 23, x ∈ I}

Solving for P,

5 < 2x – 1 ≤ 11

5 + 1 < 2x ≤ 11 + 1

6 < 2x ≤ 12

3 < x ≤ 6

Hence, P = P {x : 3 < x ≤ 6, x ∈ R}

Representing the solution on a number line:

Next, solving for Q

– 1 ≤ 3 + 4x < 23

-1 – 3 ≤ 4x < 23 – 3

-4 ≤ 4x < 20

-1 ≤ x < 5

Hence, solution Q = {-1, 0, 1, 2, 3, 4}

Representing the solution on a number line:

Therefore, P ∩ Q = {4}

29. If x ∈ I, find the smallest value of x which satisfies the inequation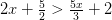 
Solution:

Given inequation,

(4x + 5)/2 > (5x + 6)/3 [Taking L.C.M]

3 (4x + 5) > 2 (5x + 6) [On cross-multiplication]

12x + 15 > 10x + 12

12x – 10x > 12 – 15

2x > -3

x > -3/2

Hence, for x ∈ I the smallest value of x is -1.

30. Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when
(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N.
Solution:

Given inequation, 20 – 5 x < 5 (x + 8)

20 – 5x < 5x + 40

-5x – 5x < 40 – 20

-10x < 20

-x < 20/10

x > -2

Thus,

(i) For x ∈ I, the smallest value = -1

(ii) For x ∈ W, the smallest value = 0

(iii) For x ∈ N, the smallest value = 1

31. Solve the following inequation and represent the solution set on the number line:

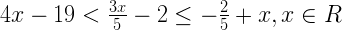
Solution:

Given inequation,

So, we have

4x – 19 < 3x/5 – 2 and 3x/5 – 2 ≤ -2/5 + x

4x – 3x/5 < 19 – 2 and 3x/5 – x ≤ 2 – 2/5

(20x – 3x)/5 < 17 and (3x – 5x)/5 ≤ (10 – 2)/5

17x < 35 and -2x ≤ 8 [Multiplying by 5]

x < 5 and -x ≤ 4

x < 5 and x ≥ 4

-4 ≤ x < 5, x ∈ R

Hence, the solution set is {x : -4 ≤ x < 5, x ∈ R}

Representing the solution on a number line:

32. Solve the given inequation and graph the solution on the number line:
2y – 3 < y + 1 ≤ 4y + 7;
y ∈ R.
Solution:

Given inequation, 2y – 3 < y + 1 ≤ 4y + 7

So, we have

2y – 3 < y + 1 and y + 1 ≤ 4y + 7

2y – y < 1 + 3 and y – 4y ≤ 7 – 1

y < 4 and -3y ≤ 6

y < 4 and -y ≤ 2 ⇒ y ≥ -2

Thus, -2 ≤ y < 4

The solution set is {y : -2 ≤ y < 4, y ∈ R}

Representing the solution on a number line:

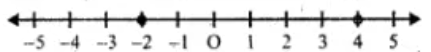
33. Solve the inequation and represent the solution set on the number line.

Solution:

Given inequation,

So, we have

-3 + x ≤ 8x/3 + 2 and 8x/3 + 2 ≤ 14/3 + 2x

x – 8x/3 ≤ 2 + 3 and 8x/3 – 2x ≤ 14/3 – 2

(3x – 8x)/3 ≤ 5 and (8x – 6x)/3 ≤ (14 – 6)/3 [Taking L.C.M]

-5x/3 ≤ 5 and 2x ≤ 8

-5x ≤ 15 and x ≤ 8/2

-x ≤ 3 and x ≤ 4

x ≥ -3 and x ≤ 4

⇒ -3 ≤ x ≤ 4

Thus, the solution set is {-3, -2, -1, 0, 1, 2, 3, 4}

Representing the solution on a number line:

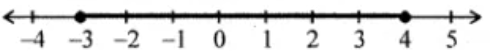
34. Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer.
Solution:

Let’s consider the greatest integer to be x

Then according to the given condition, we have

2x + 7 > 3x

2x – 3x > -7

-x > -7

x < 7 , x ∈ R

Hence, the greatest integer value is 6.

35. One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
Solution:

Let’s assume the length of the shortest pole = x metre

Now,

Length of the pole which is buried in mud = x/3

Length of the pole which is in the water = x/6

Then according to the given condition, we have

x – [x/3 + x/6] ≥ 3

x – [(2x + x)/6] ≥ 3

x – 3x/6 ≥ 3

x – x/2 ≥ 3

x/2 ≥ 3

x ≥ 6 [Multiplying by 6]

Therefore, the length of the shortest pole is 6 metres.

Chapter Test

1. Solve the inequation: 5x – 2 ≤ 3 (3 – x) where x ∈ {-2, -1, 0, 1, 2, 3, 4}. Also represent its solution on the number line.

Solution:

Given inequation, 5x – 2 ≤ 3 (3 – x)

5x – 2 ≤ 9 – 3x

5x + 3x ≤ 9 + 2

8x ≤ 11

x ≤ 11/8

As x ∈ {-2, -1, 0, 1, 2, 3, 4}

The solution set is {-2, -1, 0, 1}

Representing the solution on a number line:

2. Solve the inequation: 6x – 5 < 3x + 4, x ∈ I

Solution:

Given inequation, 6x – 5 < 3x + 4

6x – 3x < 4 + 5

3x < 9

x < 9/3

x < 3

As x ∈ I

The solution set is {2, 1, 0, -1, -2, …}

3. Find the solution set of the inequation x + 5 ≤ 2x + 3; x ∈ R

Graph the solution set on the number line.

Solution:

Given inequation, x + 5 ≤ 2x + 3

x – 2x ≤ 3 – 5

-x ≤ -2

x ≥ 2

As x ∈ R

Thus, the solution set is {2, 3, 4, 5, …}

Representing the solution on a number line:

4. If x ∈ R (real numbers) and -1 < 3 – 2x ≤ 7, find solution set and present it on a number line.

Solution:

Given inequation, -1 < 3 – 2x ≤ 7

-1 – 3 < -2x ≤ 7 – 3

-4 < -2x ≤ 4

-4/2 < -x ≤ 4/2

-2 < -x ≤ 2

Thus, -2 ≤ x < 2

The solution set is {x : x ∈ R, -2 ≤ x < 2}

Representing the solution on a number line:

5. Solve the inequation:

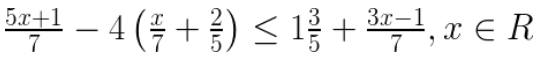
Solution:

Given inequation,

(5x + 1)/7 – 4 (5x + 14)/35 ≤ 8/5 + (3x – 1)/7

(25x + 5 – 20x – 56) ≤ 56 + 15x – 5

5x – 51 ≤ 51 + 15x

5x – 15x ≤ 51 + 51

-10x ≤ 102

-x ≤ 102/10

x ≥ – 51/5

Hence, the solution set is {x : x ∈ R , x ≥ – 51/5}

6. Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.

Solution:

7 < – 4x + 2 < 12

7 < – 4x + 2 and – 4x + 2 < 12

7. If x ∈ R, solve 2x – 3 ≥ x + (1 – x)/3 > 2x/5

Solution:

Given inequation, 2x – 3 ≥ x + (1 – x)/3 > 2x/5

So, we have

2x – 3 ≥ x + (1 – x)/3 and x + (1 – x)/3 > 2x/5

2x – 3 ≥ (3x + 1 – x)/3 and (3x + 1 – x)/3 > 2x/5 [On taking L.C.M]

3(2x – 3) ≥ 2x + 1 and (2x + 1) × 5 > 2x × 3 [Upon cross multiplication]

6x – 9 ≥ 2x + 1 and 10x + 5 > 6x

6x – 2x ≥ 1 + 9 and 10x – 6x > -5

4x ≥ 10 and 4x > -5

x ≥ 10/4 and x > -5/4

x ≥ 5/2

As x ∈ R

Thus, the solution set is {x: x ∈ R, x ≥ 5/2}

Representing the solution on a number line:

7. If x ∈ R, solve 2x – 3 ≥ x + (1 – x)/3 > 2x/5. Also represent the solution on the number line.

Solution:

Given inequation, 2x – 3 ≥ x + (1 – x)/3 > 2x/5

So, we have

2x – 3 ≥ x + (1 – x)/3 and x + (1 – x)/3 > 2x/5

2x – 3 ≥ (3x + 1 – x)/3 and (3x + 1 – x)/3 > 2x/5 [On taking L.C.M]

3 (2x – 3) ≥ 2x + 1 and 5 × (2x + 1) > 3 × 2x

6x – 9 ≥ 2x + 1 and 10x + 5 > 6x

6x – 2x ≥ 1 + 9 and 10x – 6x > -5

4x ≥ 10 and 4x > -5

x ≥ 10/4 and x > -5/4

x ≥ 5/2

As x ∈ R

The solution set = {x: x ∈ R, x ≥ 5/2}

Representing the solution on a number line:

8. Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.

Solution:

Let’s consider the positive integer be x

Then according to the problem, we have

5a – 6 < 4x

5a – 4x < 6

⇒ x < 6

Hence, the solution set = {x : x < 6}

= { 1, 2, 3, 4, 5, 6}

9. Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.

Solution:

Let’s consider the first least natural number as x

Then, second number = x + 1

And third number = x + 2

So, according the conditions given in the problem, we have

1/3 × (x + 2) – x/5 ≥ 3

5x + 10 – 3x ≥ 3 × 15

2x ≥ 45 – 10

2x ≥ 35

x ≥ 35/2

x ≥ 17.5

As x is a natural least number

Thus, first least natural number = 18

Second number = 18 + 1 = 19

And, third number = 18 + 2 = 20

Hence, the least natural numbers are 18, 19 and 20