ICSE Class 10 Sample Question Paper Maths 2017 With Answers | Specimen Papers Maths 2017 - Free PDF Download

ICSE Class 10 Maths 2017 Sample Question Paper with Answers are available at BYJU’S in a pdf format that can be downloaded easily and accessed online for free. Students can practise ICSE Maths Specimen Papers 2017 Solved for Class 10 provided at BYJU’S once they are thorough with the syllabus of ICSE class 10 Maths. They can get detailed explanations for this sample paper so that no external assistance will be required to understand the logic in solving them.

Besides the solutions of ICSE sample paper of class 10 maths 2017, students can also access important class 10 maths formulas which will help them in practising more sample papers for class 10 maths as a part of their preparation. The simple trick for the students to score maximum marks in maths is practice.

SECTION A

Attempt all questions from this section.

Question 1

(a) Find the value of a and b if x – 1 and x – 2 are factors of x³ – ax + b. [3]

Solution:

Given,

x – 1 and x – 2 are factors of x³ – ax + b.

Let p(x) = x³ – ax + b

p(1) = 0

(1)³ – a(1) + b = 0

1 – a + b = 0

a = b + 1….(i)

p(2) = 0

(2)³ – a(2) + b = 0

8 – 2a + b = 0

8 – 2(b + 1) + b = 0 [From (i)]

8 – 2b – 2 + b = 0

6 – b = 0

b = 6

Substituting b = 6 in (i),

a = 6 + 1 = 7

Therefore, a = 7 and b = 6.

(b) In the figure given below, ABCD is a parallelogram. E is a point on AB. CE intersects the diagonal BD at G and EF is parallel to BC.

If AE : EB = 1 : 2, find

(i) EF : AD

(ii) area of triangle BEF : area of triangle ABD

Solution:

In triangle BEF and ABD,

∠EBF = ∠ ABD

∠FEB = ∠BAD

∠ADB = ∠EFB

By AAA similarity criterion,

ΔBEF ~ ΔABD

By BPT,

BE/AB = EF/AD

BE/(AE + EB) = EF/AD

2/(1 + 2) = EF/AD [given AE/EB = 1/2]

EF/AD = 2/3

EF : AD = 2 : 3

(ii) The ratio of area of two similar triangles is equal to the ratio of squares of their corresponding sides.

area of triangle BEF/ area of triangle BAD = EF²/AD²

= (2/3)²

= 4/9

(c) On a certain sum of money, the difference between the compound interest for a year, payable half-yearly, and the simple interest for a year is Rs. 16. Find the sum lent out, if the rate of interest in both cases is 8%. [4]

Solution:

Given,

Rate of interest = 8%

Let P be the sum lent out for interest.

SI = PTR/100

SI = (P × 1 × 8)/100

SI = 2P/25….(i)

CI = P[1 + (R/200)]² – P (half-yearly payable)

= P[1 + (8/200)]² – P

= P(208/200)² – P

= P(43264/40000) – P

CI = 3264P/40000….(ii)

CI – SI = Rs. 16 (given)

(3264P/40000) – (2P/25) = 16

0.0816P – 0.08P = 16

0.0016P = 16

P = 16/0.0016

P = 10000

Therefore, the sum lent out is Rs. 10000.

Question 2

(a) Plot the points A(9, 6) and B(5, 9) on the graph paper. These two points are the vertices of a figure ABCD which is symmetrical about x = 5 and y = 6. Complete the figure on the graph. Write down the geometrical name of the figure. [3]

Solution:

Coordinates of C(1, 6) and D(5, 3).

The obtained figure is a rhombus.

(b) In the diagram given below ∠EDC. The tangent drawn to the circle at C makes an angle of 50° with AB produced. Find the measure of ∠ACB.

Solution:

Given,

∠AGC = 50°

AC = Diameter of the circle

∠ACG = 90° (radius is perpendicular to the tangent through the point of contact)

In triangle ACG,

∠ACG + ∠AGC + ∠CAG = 180°

90° + 50° + ∠CAG = 180°

∠CAG = 180° – 140°

∠CAG = 40°

also, ∠CAG = ∠CAB = 40°

In triangle ABC,

∠ABC = 90° (angle in a semicircle)

By the angle sum property of triangle,

∠ABC + ∠ACB + ∠CAB = 180°

90° + ∠ACB + 40 = 180°

∠ACB = 180° – 130°

∠ACB = 50°

(c) PQRS is a square piece of land of side 56 m. Two semicircular grass-covered lawns are made on two of its opposite sides as shown in the figure. Calculate the area of the uncovered portion. [4]

Solution:

Given,

Side of square PQRS = a = 56 m

Diameter of semicircle = 56 m

Radius of semicircle = r = 56/2 = 28 m

Area of the uncovered portion = Area of the square – 2 × Area of the semicircle

= a² – 2 × (πr²/2)

= (56)² – (22/7) × 28 × 28

= 3136 – 2464

= 672 m²

Question 3

(a)

Solution:

Given,

(b) A point P(a, b) is reflected in the Y-axis to P¹(-3, 1)

Write down the values of a and b.

P¹¹ is the image of P when reflected in the X-axis.

Write down the coordinates of P¹¹.

P¹¹¹ is the image of P when reflected in the line X = 5.

Write down the coordinates of P¹¹¹. [3]

Solution:

Given,

P(a, b) is reflected in the Y-axis to P¹(-3, 1).

P¹¹ is the image of P when reflected in the X-axis.

P¹¹¹ is the image of P when reflected in the line X = 5.

Coordinates of P(3, 1)

Thus, a = 3, b = 1

Coordinates of P¹¹ = (3, -1)

Coordinates of P¹¹¹ = (7, 1)

(c) Given: A = {x : 3 < 2x – 1 < 9, x ∈ R}, B = {x : 11 ≤ 3x + 2 ≤ 23, x ∈ R} where R is the set of real numbers.

(i) Represent A and B on the number line

(ii) On the number line also mark A ⋂ B. [4]

Solution:

A = {x : 3 < 2x – 1 < 9, x ∈ R}

3 < 2x – 1

3 + 1 < 2x

4 < 2x

x > 4/2

x > 2

And

2x – 1 < 9

2x < 9 + 1

x < 10/2

x < 5

Therefore, 2 < x < 5

A = {3, 4}

B = {x : 11 ≤ 3x + 2 ≤ 23, x ∈ R}

11 ≤ 3x + 2

11 – 2 ≤ 3x

9 ≤ 3x

3 ≤ x

And

3x + 2 ≤ 23

3x ≤ 23 – 2

3x ≤ 21

x ≤ 7

Therefore, 3 ≤ x ≤ 7

B = {3, 4, 5, 6, 7}

A ⋂ B = {3, 4} ⋂ {3, 4, 5, 6, 7} = {3, 4}

Question 4:

(a) Without using a trigonometric table calculate:

4 (sin 32°/ cos 58°) + 5 (tan 48°/ cot 42°) – 8 (sec 72°/ cosec 18°) [3]

Solution:

4 (sin 32°/ cos 58°) + 5 (tan 48°/ cot 42°) – 8 (sec 72°/ cosec 18°)

= 4 [ sin (90° – 58°)/ cos 58°] + 5 [tan (90° – 42°)/ cot 42°] – 8 [sec (90° – 18°)/ cosec 18°]

= 4 (cos 58°/ cos 58°) + 5 (cot 42°/ cot 42°) – 8 (cosec 18°/ cosec 18°)

= 4(1) + 5(1) – 8(1)

= 4 + 5 – 8

= 1

(b) Mr. Jacob has a two years recurring deposit account in State Bank of India and deposits Rs. 1500 per month. If he receives Rs. 37,875 at the time of maturity, find the rate of interest. [3]

Solution:

Given,

Principal (P)= Rs. 1500

Time = 2 years

i.e. n = 2 × 12 = 24 months

Let r be the rate of interest.

Amount received at the time of maturity = Total money deposited + Simple Interest

37875 = (P × n) + [{P × n(n + 1)} / (2 × 12)] × (r/100)

37875 = (1500 × 24) + [{1500 × 24 × 25} / 24] × (r/100)

37875 = 36000 + (900000 / 24) × (r/100)

37875 – 36000 = 37500 × (r/100)

r = (1875 × 100)/37500

r = 5

Hence, the rate of interest is 5%.

(c) Calculate the arithmetic mean, correct to one decimal place, for the following frequency distribution of marks obtained in a Geometry test.

Solution:

Mean = ∑fx/ ∑f

= 1160/50

= 23.2

Therefore, the arithmetic mean is 23.2.

SECTION B

Attempt any four questions from this section.

Question 5

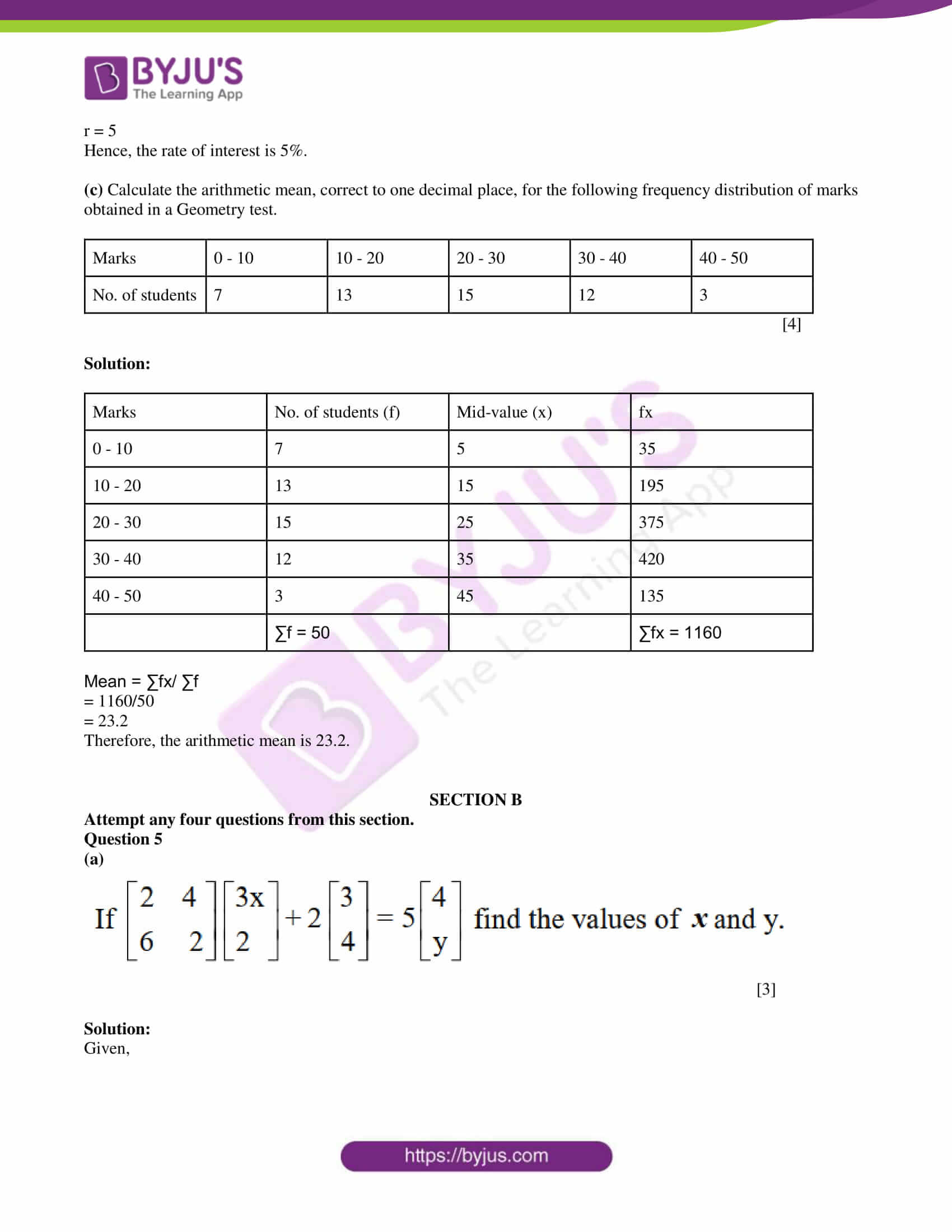
(a)

Solution:

Given,

6x + 8 = 14

6x = 14 – 8

6x = 6

x = 6/6 = 1

And

18x + 4 = 5y – 8

18(1) + 4 + 8 = 5y

5y = 30

y = 30/5 = 6

Therefore, x = 1 and y = 6.

(b) In the diagram given below, if AF = 21 cm, CE = 30 cm and FB = 7 cm. Find the volume of the figure.

Solution:

From the given figure,

Radius of cone = Radius of cylinder = Radius of hemisphere = r = 7 cm

Height of the cone = h = 21 cm

Height of the cylinder = H = 30 cm

Volume of the figure = Volume of cone + Volume of cylinder + Volume of hemisphere

= (⅓)πr²h + πr²H + (⅔)πr³

= (1/3) × (22/7) × 7 × 7 × 21 + (22/7) × 7 × 7 × 30 + (2/3) × (22/7) × 7 × 7 × 7

= 22 × 7 × 7 + 22 × 7 × 30 + (2/3) × 22 × 7 × 7

= 1078 + 4620 + 718.67

= 6416.67 cm³

(c) A man bought 200 shares each of face value Rs. 10 at Rs. 12 per share. At the end of the year, the company from which he bought the shares declares a dividend of 15%. Calculate:

(i) the amount of money invested by the man

(ii) the amount of dividend he received

(iii) the percentage return on his outlay. [4]

Solution:

Number of shares = 200

Nominal value = Rs. 10

Market value = Rs. 12

Dividend = 15%

(i) Investment = Number of shares × Market value

= Rs. 200 × 12

= Rs. 2400

(ii) Dividend = Number of shares × Percentage of dividend × Nominal value

= 200 × 15% × 10

= 200 × (15/100) × 10

= Rs. 300

(iii) Let P be the percentage of return.

Now, Dividend percentage × Nominal value = p% × Market value

15% × 10 = p% × 12

p = (15 × 10)/ 12

p = 25/2

p = 12.5

Hence, the percentage of return on outlay is 12.5%.

Question 6

(a) Solve the following quadratic equation for x and give your answer correct to three significant figures.

2x² – 4x – 3 = 0 [3]

Solution:

2x² – 4x – 3 = 0

Dividing by 2,

x² – 2x – 3/2 = 0

x² – 2x = 3/2

Adding 1 on both sides,

x² – 2x + 1 = (3/2) + 1

(x – 1)² = (5/2)

x – 1 = ± √(5/2)

x = 1 ± √(5/2)

x = 1 ± √2.5

x = 1 ± 1.581

Now,

x = 1 + 1.581, x = 1 – 1.581

x = 2.581, x = -0.581

(b) An integer is chosen at random from 1 to 50. Find the probability that the number is:

(i) divisible by 5

(ii) a perfect cube

(iii) a prime number. [3]

Solution:

Integers from 1 to 50: {1, 2, 3, 4, 5, …., 49, 50}

Total number of outcomes = n(S) = 50

(i) Number of integers divisible by 5 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50} = 10

P(getting a number that is divisible by 5) = 10/50 = 1/5

(ii) Perfect cubes = {1, 8, 27} = 3

P(getting a perfect cube number) = 3/50

(iii) Prime numbers = {2, 3,5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47} = 15

P(getting a prime number) = 15/50

= 3/10

(c) Find x from the following equation using properties of proportion:

(x² – x + 1)/ (x² + x + 1) = 14(x – 1)/ 13(x + 1) [4]

Solution:

Given,

(x² – x + 1)/ (x² + x + 1) = 14(x – 1)/ 13(x + 1)

(x² – x + 1)/ (x² + x + 1) = (14x – 14)/ (13x + 13)

Using componendo and dividendo,

(x² – x + 1 + x² + x + 1) / (x² – x + 1 – x² – x – 1) = (14x – 14 + 13x + 13)/ (14x – 14 – 13x – 13)

(2x² + 2)/ (-2x) = (27x – 1)/ (x – 27)

2(x² + 1)/ (-2x) = (27x – 1)/ (x – 27)

(x² + 1)/ (-x) = (27x – 1)/ (x – 27)

⇒ (x² + 1)(x – 27) = -x(27x – 1)

⇒ x³ – 27x² + x – 27 = -27x² + x

⇒ x³ – 27 = 0

⇒ x³ = 27

⇒ x³ = (3)³

⇒ x = 3

Question 7

(a) Bosco wishes to start a 200 m² rectangular vegetable garden. Since he has only 50 m barbed wire, he fences three sides of the rectangular garden letting his house compound wall act as the fourth side of the fence. Find the dimensions of the garden. [3]

Solution:

Let x and y be the length and breadth of the garden respectively.

According to the given,

Sum of three sides = 50 m

x + 2y = 50 m

x = 50 – 2y….(i)

Area of the garden = 200 m² (given)

xy = 200

(50 – 2y)y = 200 [From (i)]

50y – 2y² = 200

2y² – 50y + 200 = 0

2(y² – 25y + 100) = 0

y² – 25y + 100 = 0

y² – 20y – 5y + 100 = 0

y(y – 20) – 5(y – 20) = 0

(y – 5)(y – 20) = 0

y = 5, y = 20

When y = 5 m,

x = 50 – 2(5)

= 50 – 10

= 40 m

When y = 20 m,

x = 50 – 2(20)

= 50 – 40

= 10 m

Therefore, the dimensions of the garden or 40 m and 5 m or 10 m and 20 m.

(b) Construct a triangle ABC with AB = 6 cm, BC = 7 cm and ∠ABC = 60°. Locate by construction the point P such that

(i) P is equidistant from B and C

(ii) P is equidistant from AB and BC.

(iii) Measure and record the length of PA. [3]

Solution:

Length of PA is 4.5 cm. (by measure)

(c) Mr. A. Ramchander has an account with the Central Bank of India. The following entries are from his passbook.

Complete the above page of his passbook and calculate the interest accumulated in four months, January to April at the rate of 3.5% per annum. If the interest is added on 30th April, find his balance on that date. [4]

Solution:

Rate of interest = 3.5%

Let us calculate interest on the number of days in four months from 05.01.2009 to 15.04.2009.

Interest = [(8000 × 15 + 5500 × 15 + 14500 × 16 + 17500 × 12 + 16500 × 42) × 3.5]/ 365 × 100

= [(80 × 15 + 55 × 15 + 145 × 16 + 175 × 12 + 165 × 42) × 3.5]/ 365

= (1200 + 825 + 2320 + 2100 + 6930)/ 365

= 13375/ 365

= 36.64

Therefore, interest is Rs. 36.64.

Question 8

(a) Prove that [1/(sec x – tan x)] + [1/ (sec x + tan x)] = 2/cos x. [3]

Solution:

LHS = [1/(sec x – tan x)] + [1/ (sec x + tan x)]

= [sec x + tan x + sec x – tan x] / [(sec x – tan x) (sec x + tan x)]

= 2 sec x/ (sec² x – tan²x)

= 2 sec x/ 1

= 2(1/cos x)

= 2/ cos x

= RHS

Hence proved.

(b) In the figure given below, CD is the diameter of the circle which meets the chord AB at P such that AP = BP = 12 cm. If DP = 8 cm, find the radius of the circle. [3]

Solution:

Given,

AP = BP = 12 cm

DP = 8 cm

Join OA and OB.

Let OP = x

OA = OB = OD = Radius of the circle

OA = OB = OD = (8 + x) cm

In right triangle OPA,

OA² = OP² + AP²

(8 + x)² = x² + (12)²

64 + x² + 16x = x² + 144

16x = 144 – 64

16x = 80

x = 80/16

x = 5

Now,

OD = 8 + 5 = 13 cm

Therefore, the radius of the circle is 13 cm.

(c) Prove that A(2, 1), B(0, 3) and C(-2, 1) are the three vertices of an isosceles right-angled triangle. Hence, find the coordinates of a point D, if ABCD is a square. [4]

Solution:

Given,

A(2, 1), B(0, 3) and C(-2, 1)

Using distance formula,

AB = √[(0 – 2)² + (3 – 1)²]

= √(4 + 4)

= √8

BC = √[(-2 – 0)² + (1 – 3)²]

= √4 + 4)

= √8

AC = √(-2 – 2)² + (1 – 1)²]

= √(16 + 0)

= √16

Now, AB² + BC² = (√8)² + (√8)²

= 8 + 8

= 16

= AC²

Therefore, ABC is an isosceles right-angled triangle.

Let D(x, y) be the fourth vertex of square ABCD.

Midpoint of AC = Midpoint of BD

(0/2, 2/2) = [x/2, (3 + y)/2]

(0, 1) = [x/2, (3 + y)/2]

x/2 = 0, 3 + y = 2

x = 0, y = -1

Hence, the coordinates of D are (0, -1).

Question 9

(a) A fair die is rolled. Find the probability of getting

(i) 3 on the face of the dice

(ii) an odd number on the face of the dice

(iii) a number greater than 1 on the face of the dice. [3]

Solution:

Given,

A fair die is rolled.

Sample space = S = {1, 2, 3, 4, 5, 6}

n(S) = 6

(i) Let A be the event of getting 3 on the face of the die.

A = {3}

n(A) = 1

P(A) = n(A)/ n(S)

= 1/3

(ii) Let B be the event of getting an odd number.

B = {1, 3, 5}

n(B) = 3

P(B) = n(B)/ n(S)

= 3/6

= 1/2

(iii) Let C be the event of getting a number greater than 1.

C = {2, 3, 4, 5, 6}

n(C) = 5

P(C) = n(C)/ n(S)

= 5/6

(b) A(4, 2), B(6, 8) and C(8, 4) are the vertices of a triangle ABC. Write down the equation of the median of the triangle through A. [3]

Solution:

Let AD be the median of triangle ABC.

Given,

A(4, 2), B(6, 8) and C(8, 4)

D = Midpoint of BC

= [(6 + 8)/2, (8 + 4)/2]

= (14/2, 12/2)

= (7, 6)

Let A(4, 2) = (x₁, y₁)

D(7, 6) = (x₂, y₂)

Equation of line AD is

(y – y₁)/ (y₂ – y₁) = (x – x₁)/ (x₂ – x₁)

(y – 2)/ (6 – 2) = (x – 4)/ (7 – 4)

(y – 2)/ 4 = (x – 4)/ 3

3(y – 2) = 4(x – 4)

3y – 6 = 4x – 16

4x – 16 – 3y + 6 = 0

4x – 3y – 10 = 0

Hence, the equation of the median of the triangle through A is 4x – 3y – 10 = 0.

(c) The angle of elevation of an aeroplane from a point P on the ground is 60°. After 12 seconds from the same point P, the angle of elevation of the same plane changes to 30°. If the plane is flying horizontally at a speed of 600√3 km/hr, find the height at which the plane is flying. [4]

Solution:

Given,

Speed = 600√3 km/hr

Distance = Speed × Time

Distance travelled by an aeroplane in 12 seconds = 600√3 × (12/ 60 × 60)

= 2√3 km

Let A be the initial position of an aeroplane.

AC = BD = 2√3 km

CD = AB = h

In right triangle ABP,

tan 60° = AB/BP

√3 = h/x

⇒ h = √3x….(i)

In right triangle CDP,

tan 30° = CD/DP

1/√3 = h/ (2√3 + x)

2√3 + x = h√3

2√3 + x = (√3x) √3 [From (i)]

2√3 + x = 3x

⇒ 3x – x = 2√3

⇒ 2x = 2√3

⇒ x = √3

Substituting x = √3 in (i),

h = (√3) (√3)

h = 3 km

Hence, the height at which the plane is flying is 3 km.

Question 10

(a) The following table shows the distribution of the heights of a group of students:

Use a graph sheet to draw an Ogive for the distribution.

Use the Ogive to find:

(i) the interquartile range

(ii) the number of students whose height is more than 168 cm

(iii) the number of students whose height is less than 148 cm. [6]

Solution:

Ogive:

(i) Median value = (N/2)th observation = (100/2) = 50th observation = 158

Lower quartile = (N/4)th observation = (100/4) = 25th observation = 152

Upper quartile = (3N/4)th observation = (300/4) = 75th observation = 161

Inter quartile range = Upper quartile – Lower quartile

= 161 – 152

= 9

(ii) The number of students whose height is more than 168 cm = 100 – 92 = 8

(iii) The number of students whose height is less than 148 cm = 14

(b) The manufacturer sold a TV to a wholesaler for Rs. 7000. The wholesaler sold it to a trader at a profit of Rs. 1000. If the trader sold it to the customer at a profit of Rs. 1500, find:

(i) the total VAT (value added tax) collected by the state government at the rate of 5%.

(ii) the amount that the customer pays for the TV. [4]

Solution:

Cost price of TV for wholesaler = Rs. 7000

Selling price of TV to a trader from wholesaler = Rs. (7000 + 1000) = Rs. 8000

Selling price of TV from trader = Rs. (8000 + 1500) = Rs. 9500

(i) The total VAT (value added tax) collected by the state government at the rate of 5% = (5/100) × 9500 = Rs. 475

(ii) The amount the customer pays for the TV = Rs. 9500 + Rs. 475

= Rs. 9975

Question 11:

(a) In the diagram given below, the equation of AB is x – √3y + 1 = 0 and the equation of AC is x – y – 2 = 0.

(i) Write down the angles that the lines AC and AB make with the positive direction of X-axis.

(ii) Find ∠BAC. [3]

Solution:

(i) Given,

The equation of AB is x – √3y + 1 = 0.

√3y = x + 1

Slope = 1/√3

tan θ = 1/√3

tan θ = tan 30°

θ = 30°

i.e. ∠ABC = 30°

The equation of AC is x – y – 2 = 0.

y = x – 2

Slope = 1

tan θ = 1

tan θ = tan 45°

θ = 45°

i.e. ∠ACX = 45°

(ii) ∠ACB = 180° – ∠ACX = 180° – 45° = 135°

In triangle ABC,

∠ABC + ∠ACB + ∠BAC = 180°

30° + 135° + ∠BAC = 180°

∠BAC = 180° – 30° – 135°

∠BAC = 15°

(b) In the figure given below, O is the centre of the circle. Chord CD is parallel to the diameter AB. If ∠ABC = 35°, calculate ∠CED. [3]

Solution:

Given,

Chord CD is parallel to the diameter AB.

∠ABC = 35°

Angle subtended by the chord at the centre is twice the angle subtended by it on the corresponding segment of the circle.

∠AOC = 2∠ABC

= 2 × 35°

= 70°

∠AOC = ∠BOD = 70°

By linear pair axiom,

∠AOC + ∠COD + ∠BOD = 180°

70° + ∠COD + 70° = 180°

∠COD = 180° – 70° – 70°

∠COD = 140°

Now,

∠COD = 2∠CED

40° = 2∠CED

∠CED = 40°/2

∠CED = 20°

(c) Construct a triangle ABC, given that AB = 6 cm, BC = 8 cm and median AD = 5 cm. Construct an incircle to triangle ABC and measure its radius. [4]

Solution:

Measure of radius of incircle = 2 cm (approx)