ML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions are provided here to help students prepare and excel in their exams. This chapter mainly deals with problems based on expansions. Expert tutors have formulated the solutions in a step-by-step manner for students to grasp the concepts easily. From the exam point of view, by solving problems on a regular basis, students can improve their conceptual knowledge. The solutions contain brief step-wise explanations, which are purely based on the latest syllabus of the ICSE board. Students can cross-check the answers with the solutions designed by the experts and understand the other ways of solving problems effortlessly. To learn more about these concepts, students can access the ML Aggarwal Solutions PDF from the links which are provided below and start practising offline to secure good marks in the board exams.
Chapter 3 – Expansions contain a chapter test, and the ML Aggarwal Class 9 Solutions present on this page provide solutions to questions related to each topic present in this chapter.
ML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions
Access answers to ML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions
Exercise 3.1
By using standard formulae, expand the following (1 to 9):
1. (i) (2x + 7y)2
(ii) (1/2 x + 2/3 y)2
Solution:
(i) (2x + 7y)2
It can be written as
= (2x)2 + 2 × 2x × 7y + (7y)2
So we get
= 4x2 + 28xy + 49y2
(ii) (1/2 x + 2/3 y)2
It can be written as
= (1/2 x)2 + 2 × ½x + 2/3y + (2/3 y)2
So we get
= ¼ x2 + 2/3 xy + 4/9 y2
2. (i) (3x + 1/2x)2
(ii) (3x2y + 5z)2
Solution:
(i) (3x + 1/2x)2
It can be written as
= (3x)2 + 2 × 3x × 1/2x + (1/2x)2
So we get
= 9x2 + 3 + 1/4x2
= 9x2 + 1/4x2 + 3
(ii) (3x2y + 5z)2
It can be written as
= (3x2y)2 + 2 × 3x2y × 5z + (5z)2
So we get
= 9x4y2 + 30x2yz + 25z2
3. (i) (3x – 1/2x)2
(ii) (1/2 x – 3/2 y)2
Solution:
(i) (3x – 1/2x)2
It can be written as
= (3x)2 – 2 × 3x × 1/2x + (1/2x)2
So we get
= 9x2 – 3 + 1/4x2
= 9x2 + 1/4x2 – 3
(ii) (1/2 x – 3/2 y)2
It can be written as
= (1/2 x)2 + (3/2 y)2 – 2 × ½ x × 3/2 y
So we get
= ¼ x2 + 9/4 y2 – 3/2 xy
= ¼ x2 – 3/2 xy + 9/4 y2
4. (i) (x + 3) (x + 5)
(ii) (x + 3) (x – 5)
(iii) (x – 7) (x + 9)
(iv) (x – 2y) (x – 3y)
Solution:
(i) (x + 3) (x + 5)
By further calculation
= x2 + (3 + 5) x + 3 × 5
So we get
= x2 + 8x + 15
(ii) (x + 3) (x – 5)
By further calculation
= x2 + (3 – 5)x – 3 × 5
So we get
= x2 – 2x – 15
(iii) (x – 7) (x + 9)
By further calculation
= x2 – (7 – 9)x – 7 × 9
So we get
= x2 + 2x – 63
(iv) (x – 2y) (x – 3y)
By further calculation
= x2 – (2y + 3y)x + 2y × 3y
So we get
= x2 – 5xy + 6y2
5. (i) (x – 2y – z)2
(ii) (2x – 3y + 4z)2
Solution:
(i) (x – 2y – z)2
It can be written as
= [x + (-2y) + (-z)]2
By further calculation
= (x)2 + (-2y)2 + (-z)2 + 2 × x × (-2y) + 2 × (-2y) × (-z) + 2 × (-z) × x
So we get
= x2 + 4y2 + z2 – 4xy + 4yz – 2zx
(ii) (2x – 3y + 4z)2
It can be written as
= [2x + (-3y) + 4z]2
By further calculation
= (2x)2 + (-3y)2 + (4z)2 + 2 × 2x × (-3y) + 2 × (-3y) × 4z + 2 × 4z × 2x
So we get
= 4x2 + 9y2 + 16z2 -12xy – 24yz + 16zx
6. (i) (2x + 3/x – 1)2
(ii) (2/3 x – 3/2x – 1)2
Solution:
(i) (2x + 3/x – 1)2
It can be written as
= [2x + 3/x + (-1)]2
By further calculation
= (2x)2 + (3/x)2 + (-1)2 + 2 ×2x × 3/x + 2 × 3/x × (-1) + 2 × (-1) × 2x
So we get
= 4x2 + 9/x2 + 1 + 12 – 6/x – 4x
= 4x2 + 9/x2 + 13 – 6/x – 4x
(ii) (2/3 x – 3/2x – 1)2
It can be written as
= [2/3 x – 3/2x – 1]2
By further calculation
= (2/3 x)2 + (-3/2x)2 + (-1)2 + 2 × 2/3 x × (-3/2x) + 2 × (-3/2x) × (-1) + 2 × (-1) × (2/3 x)
So we get
= 4/9 x2 + 9/4x2 + 1 – 2 + 3/x – 4/3 x
= 4/9 x2 + 9/4x2 – 1 – 4/3 x + 3/x
7. (i) (x + 2)3
(ii) (2a + b)3
Solution:
(i) (x + 2)3
It can be written as
= x3 + 23 + 3 × x × 2 (x + 2)
By further calculation
= x3 + 8 + 6x (x + 2)
So we get
= x3 + 8 + 6x2 + 12x
= x3 + 6x2 + 12x + 8
(ii) (2a + b)3
It can be written as
= (2a)3 + b3 + 3 × 2a × b (2a + b)
By further calculation
= 8a3 + b3 + 6ab (2a + b)
So we get
= 8a3 + b3 + 12a2b + 6ab2
8. (i) (3x + 1/x)3
(ii) (2x – 1)3
Solution:
(i) (3x + 1/x)3
It can be written as
= (3x)3 + (1/x)3 + 3 × 3x × 1/x (3x + 1/x)
By further calculation
= 27x3 + 1/x3 + 9 (3x + 1/x)
So we get
= 27x3 + 1/x3 + 27x + 9/x
(ii) (2x – 1)3
It can be written as
= (2x)3 – 13 – 3 × 2x × 1 (2x – 1)
By further calculation
= 8x3 – 1 – 6x (2x – 1)
So we get
= 8x3 – 1 – 12x2 + 6x
= 8x3 – 12x2 + 6x – 1
9. (i) (5x – 3y)3
(ii) (2x – 1/3y)3
Solution:
(i) (5x – 3y)3
It can be written as
= (5x)3 – (3y)3 – 3 × 5x × 3y (5x – 3y)
By further calculation
= 125x3 – 27y3 – 45xy (5x – 3y)
So we get
= 125x3 – 27y3 – 225x2y + 135xy2
(ii) (2x – 1/3y)3
It can be written as
= (2x)3 – (1/3y)3 – 3 × 2x × 1/3y (2x – 1/3y)
By further calculation
= 8x3 – 1/27y3 – 2x/y (2x – 1/3y)
So we get
= 8x3 – 1/27y3 – 4x2/y + 2x/3y2
Simplify the following (10 to 19):
10. (i) (a + b)2 + (a – b)2
(ii) (a + b)2 – (a – b)2
Solution:
(i) (a + b)2 + (a – b)2
It can be written as
= (a2 + b2 + 2ab) + (a2 +b2 – 2ab)
By further calculation
= a2 + b2 + 2ab + a2 + b2 – 2ab
So we get
= 2a2 + 2b2
Taking 2 as common
= 2 (a2 + b2)
(ii) (a + b)2 – (a – b)2
It can be written as
= (a2 + b2 + 2ab) – (a2 + b2 – 2ab)
By further calculation
= a2 + b2 + 2ab – a2 – b2 + 2ab
So we get
= 4ab
11. (i) (a + 1/a)2 + (a – 1/a)2
(ii) (a + 1/a)2 – (a – 1/a)2
Solution:
(i) (a + 1/a)2 + (a – 1/a)2
It can be written as
= [a2 + (1/a)2 + 2 × a × 1/a] + [a2 + (1/a)2 – 2 × a × 1/a]
By further calculation
= [a2 + 1/a2 + 2] + [a2 + 1/a2 – 2]
So we get
= a2 + 1/a2 + 2 + a2 + 1/a2 – 2
= 2a2 + 2/a2
Taking 2 as common
= 2 (a2 + 1/a2)
(ii) (a + 1/a)2 – (a – 1/a)2
It can be written as
= [a2 + (1/a)2 + 2 × a × 1/a] – [a2 + (1/a)2 – 2 × a × 1/a]
By further calculation
= [a2 + 1/a2 + 2] – [a2 + 1/a2 – 2]
So we get
= a2 + 1/a2 + 2 – a2 – 1/a2 + 2
= 4
12. (i) (3x – 1)2 – (3x – 2) (3x + 1)
(ii) (4x + 3y)2 – (4x – 3y)2 – 48xy
Solution:
(i) (3x – 1)2 – (3x – 2) (3x + 1)
It can be written as
= [(3x)2 + 12 – 2 × 3x × 1] – [(3x)2 – (2 – 1) (3x) – 2 × 1]
By further calculation
= [9x2 + 1 – 6x] – [9x2 – 3x – 2]
So we get
= 9x2 + 1 – 6x – 9x2 + 3x + 2
= -3x + 3
= 3 – 3x
(ii) (4x + 3y)2 – (4x – 3y)2 – 48xy
It can be written as
= [(4x)2 + (3y)2 + 2 × 4x × 4y] – [(4x)2 + (3y)2 – 2 × 4x × 3y] – 48xy
By further calculation
= [16x2 + 9y2 + 24xy] – [16x2 + 9y2 – 24xy] – 48xy
So we get
= 16x2 + 9y2 + 24xy – 16x2 – 9y2 + 24xy – 48xy
= 0
13. (i) (7p + 9q) (7p – 9q)
(ii) (2x – 3/x) (2x + 3/x)
Solution:
(i) (7p + 9q) (7p – 9q)
It can be written as
= (7p)2 – (9q)2
= 49p2 – 81q2
(ii) (2x – 3/x) (2x + 3/x)
It can be written as
= (2x)2 – (3/x)2
= 4x2 – 9/x2
14. (i) (2x – y + 3) (2x – y – 3)
(ii) (3x + y – 5) (3x – y – 5)
Solution:
(i) (2x – y + 3) (2x – y – 3)
It can be written as
= [(2x – y) + 3] [(2x – y) – 3]
= (2x – y)2 – 32
By further calculation
= (2x)2 +y2 – 2 × 2x × y – 9
So we get
= 4x2 + y2 – 4xy – 9
(ii) (3x + y – 5) (3x – y – 5)
It can be written as
= [(3x – 5) + y] [(3x – 5) – y]
= (3x – 52) – y2
By further calculation
= (3x)2 + 52 – 2 × 3x × 5 – y2
So we get
= 9x2 + 25 – 30x – y2
= 9x2 – y2 – 30x + 25
15. (i) (x + 2/x – 3) (x – 2/x – 3)
(ii) (5 – 2x) (5 + 2x) (25 + 4x2)
Solution:
(i) (x + 2/x – 3) (x – 2/x – 3)
It can be written as
= [(x – 3) + (2/x)] [(x – 3) – (2/x)]
= (x – 3)2 – (2/x)2
Expanding using formula
= x2 + 9 – 2 × x × 3 – 4/x2
By further calculation
= x2 + 9 – 6x – 4/x2
So we get
= x2 – 4/x2 – 6x + 9
(ii) (5 – 2x) (5 + 2x) (25 + 4x2)
It can be written as
= [52 – (2x)2] (25 + 4x2)
By further calculation
= (25 – 4x2) (25 + 4x2)
So we get
= 252 – (4x2)2
= 625 – 16x4
16. (i) (x + 2y + 3) (x + 2y + 7)
(ii) (2x + y + 5) (2x + y – 9)
(iii) (x – 2y – 5) (x – 2y + 3)
(iv) (3x – 4y – 2) (3x – 4y – 6)
Solution:
(i) (x + 2y + 3) (x + 2y + 7)
Consider x + 2y = a
(a + 3) (a + 7) = a2 + (3 + 7) a + 3 × 7
By further calculation
= a2 + 10a + 21
Substituting the value of a
= (x + 2y)2 + 10 (x + 2y) + 21
By expanding using formula
= x2 + 4y2 + 2 × x × 2y + 10x + 20y + 21
So we get
= x2 + 4y2 + 4xy + 10x + 20y + 21
(ii) (2x + y + 5) (2x + y – 9)
Consider 2x + y = a
(a + 5) (a – 9) = a2 + (5 – 9) a + 5 × (-9)
By further calculation
= a2 – 4a – 45
Substituting the value of a
= (2x + y)2 – 4 (2x + y) – 45
By expanding using formula
= 4x2 + y2 + 2 × 2x × y – 8x – 4y – 45
So we get
= 4x2 + y2 + 4xy – 8x – 4y – 45
(iii) (x – 2y – 5) (x – 2y + 3)
Consider x – 2y = a
(a – 5) (a + 3) = a2 + (- 5 + 3) a + (-5) (3)
By further calculation
= a2 – 2a – 15
Substituting the value of a
= (x – 2y)2 – 2 (x – 2y) – 15
By expanding using formula
= x2 + 4y2 – 2 × x × 2y – 2x + 4y – 15
So we get
= x2 + 4y2 – 4xy – 2x + 4y – 15
(iv) (3x – 4y – 2) (3x – 4y – 6)
Consider 3x – 4y = a
(a – 2) (a – 6) = a2 (- 2 – 6)a + (-2) (-6)
By further calculation
= a2 – 8a + 12
Substituting the value of a
= (3x – 4y)2 – 8 (3x – 4y) + 12
Expanding using formula
= 9x2 + 16y2 – 2 × 3x × 4y – 24x + 32y + 12
So we get
= 9x2 + 16y2 – 24xy – 24x + 32y + 12
17. (i) (2p + 3q) (4p2 – 6pq + 9q2)
(ii) (x + 1/x) (x2 – 1 + 1/x2)
Solution:
(i) (2p + 3q) (4p2 – 6pq + 9q2)
It can be written as
= (2p + 3q) [(2p)2 – 2p × 3q + (3q)2]
By further simplification
= (2p)3 + (3q)3
= 8p3 + 27q3
(ii) (x + 1/x) (x2 – 1 + 1/x2)
It can be written as
= (x + 1/x) [x2 – x × 1/x + (1/x)2]
By further simplification
= x3 + (1/x)3
= x3 + 1/x3
18. (i) (3p – 4q) (9p2 + 12pq + 16q2)
(ii) (x – 3/x) (x2 + 3 + 9/x2)
Solution:
(i) (3p – 4q) (9p2 + 12pq + 16q2)
It can be written as
= (3p – 4q) [(3p)2 + 3p × 4q + (4q)2]
By further simplification
= (3p)3 – (4q)3
= 27p3 – 64q3
(ii) (x – 3/x) (x2 + 3 + 9/x2)
It can be written as
= (x – 3/x) [x2 + x × 3/x + (3/x)2]
By further simplification
= x3 – (3/x)3
= x3 – 27/x3
19. (2x + 3y + 4z) (4x2 + 9y2 + 16z2 – 6xy – 12yz – 8zx).
Solution:
(2x + 3y + 4z) (4x2 + 9y2 + 16z2 – 6xy – 12yz – 8zx)
It can be written as
= (2x + 3y + 4z) ((2x)2 + (3y)2 + (4z)2 – 2x × 3y – 3y × 4z – 4z × 2x)
By further calculation
= (2x)3 + (3y)3 + (4z)3 – 3 × 2x × 3y × 4z
So we get
= 8x3 + 27y3 + 64z3 – 72xyz
20. Find the product of the following:
(i) (x + 1) (x + 2) (x + 3)
(ii) (x – 2) (x – 3) (x + 4)
Solution:
(i) (x + 1) (x + 2) (x + 3)
It can be written as
= x3 + (1 + 2 + 3)x2 + (1 × 2 + 2 × 3 + 3 × 1) x + 1 × 2 × 3
By further calculation
= x3 + 6x2 + (2 + 6 + 3)x + 6
So we get
= x3 + 6x2 + 11x + 6
(ii) (x – 2) (x – 3) (x + 4)
It can be written as
= x3 + (- 2 – 3 + 4) x2 + [(-2) × (-3) + (-3) × 4 + 4 × (-2)]x + (-2) (-3) (4)
By further calculation
= x3 – x2 + (6 – 12 – 8)x + 24
= x3 – x2 – 14x + 24
21. Find the coefficient of x2 and x in the product of (x – 3) (x + 7) (x – 4).
Solution:
It is given that
(x – 3) (x + 7) (x – 4)
By further calculation
= x3 + (- 3 + 7 – 4) x2 + [(-3) (7) + 7 × (-4) + (-4) (-3) + (-3) (7) (-4)]
It can be written as
= x3 + 0x2 + (- 21 – 28 + 12) x + 84
So we get
= x3 + 0x2 – 37x + 84
Hence, the coefficient of x2 is zero and the coefficient of x is – 3.
22. If a2 + 4a + x = (a + 2)2, find the value of x.
Solution:
It is given that
a2 + 4a + x = (a + 2)2
By expanding using the formula
a2 + 4a + x = a2 + 22 + 2 × a × 2
By further calculation
a2 + 4a + x = a2 + 4 + 4a
So we get
x = a2 + 4 + 4a – a2 – 4a
x = 4
23. Use (a + b)2 = a2 + 2ab + b2 to evaluate the following:
(i) (101)2
(ii) (1003)2
(iii) (10.2)2
Solution:
(i) (101)2
It can be written as
= (100 + 1)2
Expanding using formula
= 1002 + 12 + 2 × 100 × 1
By further calculation
= 10000 + 1 + 200
= 10201
(ii) (1003)2
It can be written as
= (1000 + 3)2
Expanding using formula
= 10002 + 32 + 2 × 1000 × 3
By further calculation
= 1000000 + 9 + 6000
= 1006009
(iii) (10.2)2
It can be written as
= (10 + 0.2)2
Expanding using formula
= 102 + 0.22 + 2 × 10 × 0.2
By further calculation
= 100 + 0.04 + 4
= 104.04
24. Use (a – b)2 = a2 – 2ab – b2 to evaluate the following:
(i) (99)2
(ii) (997)2
(iii) (9.8)2
Solution:
(i) (99)2
It can be written as
= (100 – 1)2
Expanding using formula
= 1002 – 2 × 100 × 1 + 12
By further calculation
= 10000 – 200 + 1
= 9801
(ii) (997)2
It can be written as
= (1000 – 3)2
Expanding using formula
= 10002 – 2 × 1000 × 3 + 32
By further calculation
= 1000000 – 6000 + 9
= 994009
(iii) (9.8)2
It can be written as
= (10 – 0.2)2
Expanding using formula
= 102 – 2 × 10 × 0.2 + 0.22
By further calculation
= 100 – 4 + 0.04
= 96.04
25. By using suitable identities, evaluate the following:
(i) (103)3
(ii) (99)3
(iii) (10.1)3
Solution:
(i) (103)3
It can be written as
= (100 + 3)3
Expanding using formula
= 1003 + 33 + 3 × 100 × 3 (100 + 3)
By further calculation
= 1000000 + 27 + 900 × 103
So we get
= 1000000 + 27 + 92700
= 1092727
(ii) (99)3
It can be written as
= (100 – 1)3
Expanding using formula
= 1003 – 13 – 3 × 100 × 1 (100 – 1)
By further calculation
= 1000000 – 1 – 300 × 99
So we get
= 1000000 – 1 – 29700
= 1000000 – 29701
= 970299
(iii) (10.1)3
It can be written as
= (10 + 0.1)3
Expanding using formula
= 103 + 0.13 + 3 × 10 × 0.1 (10 + 0.1)
By further calculation
= 1000 + 0.001 + 3 × 10.1
So we get
= 1000 + 0.001 + 30.3
= 1030.301
26. If 2a – b + c = 0, prove that 4a2 – b2 + c2 + 4ac = 0.
Solution:
It is given that
2a – b + c = 0
2a + c = b
By squaring on both sides
(2a + c)2 = b2
Expanding using formula
(2a)2 + 2 × 2a × c + c2 = b2
By further calculation
4a2 + 4ac + c2 = b2
So we get
4a2 – b2 + c2 + 4ac = 0
Hence, it is proved.
27. If a + b + 2c = 0, prove that a3 + b3 + 8c3 = 6abc.
Solution:
It is given that
a + b + 2c = 0
We can write it as
a + b = – 2c
By cubing on both sides
(a + b)3 = (-2c)3
Expanding using formula
a3 + b3 + 3ab (a + b) = -8c3
Substituting the value of a + b
a3 + b3 + 3ab (-2c) = -8c3
So we get
a3 + b3 + 8c3 = 6abc
Hence, it is proved.
28. If a + b + c = 0, then find the value of a2/bc + b2/ca + c2/ab.
Solution:
It is given that
a + b + c = 0
We can write it as
a3 + b3 + c3 – 3abc = 0
a3 + b3 + c3 = 3abc
Now dividing by abc on both sides
a3/abc + b3/abc + c3/abc = 3
By further calculation
a2/bc + b2/ac + c2/ab = 3
Therefore, the value of a2/bc + b2/ca + c2/ab is 3.
29. If x + y = 4, then find the value of x3 + y3 + 12xy – 64.
Solution:
It is given that
x + y = 4
By cubing on both sides
(x + y)3 = 43
Expanding using formula
x3 + y3 + 3xy (x + y) = 64
Substituting the value of x + y
x3 + y3 + 3xy (4) = 64
So we get
x3 + y3 + 12xy – 64 = 0
Hence, the value of x3 + y3 + 12xy – 64 is 0.
30. Without actually calculating the cubes, find the values of:
(i) (27)3 + (-17)3 + (-10)3
(ii) (-28)3 + (15)3 + (13)3
Solution:
(i) (27)3 + (-17)3 + (-10)3
Consider a = 27, b = – 17 and c = – 10
We know that
a + b + c = 27 – 17 – 10 = 0
So a + b + c = 0
a3 + b3 + c3 = 3abc
Substituting the values
273 + (-17)3 + (-10)3 = 3 (27) (-17) (- 10)
= 13770
(ii) (-28)3 + (15)3 + (13)3
Consider a = – 28, b = 15 and c = 13
We know that
a + b + c = – 28 + 15 + 13 = 0
So a + b + c = 0
a3 + b3 + c3 = 3abc
Substituting the values
(-28)3 + (15)3 + (13)3 = 3 (- 28) (15) (13)
= – 16380
31. Using suitable identity, find the value of:

Solution:
Consider x = 86 and y = 14
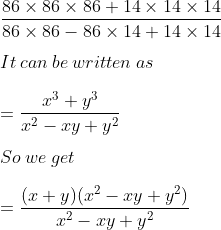
= x + y
Substituting the values
= 86 + 14
= 100
Exercise 3.2
1. If x – y = 8 and xy = 5, find x2 + y2.
Solution:
We know that
(x – y)2 = x2 + y2 – 2xy
It can be written as
x2 + y2 = (x – y)2 + 2xy
It is given that
x – y = 8 and xy = 5
Substituting the values
x2 + y2 = 82 + 2 × 5
So we get
= 64 + 10
= 74
2. If x + y = 10 and xy = 21, find 2 (x2 + y2).
Solution:
We know that
(x + y)2 = x2 + y2 + 2xy
It can be written as
x2 + y2 = (x + y)2 – 2xy
It is given that
(x + y) = 10 and xy = 21
Substituting the values
x2 + y2 = 102 – 2 × 21
By further calculation
= 100 – 42
= 58
Here
2 (x2 + y2) = 2 × 58 = 116
3. If 2a + 3b = 7 and ab = 2, find 4a2 + 9b2.
Solution:
We know that
(2a + 3b)2 = 4a2 + 9b2 + 12ab
It can be written as
4a2 + 9b2 = (2a + 3b)2 – 12ab
It is given that
2a + 3b = 7
ab = 2
Substituting the values
4a2 + 9b2 = 72 – 12 × 2
By further calculation
= 49 – 24
= 25
4. If 3x – 4y = 16 and xy = 4, find the value of 9x2 + 16y2.
Solution:
We know that
(3x – 4y)2 = 9x2 + 16y2 – 24xy
It can be written as
9x2 + 16y2 = (3x – 4y)2 + 24xy
It is given that
3x – 4y = 16 and xy = 4
Substituting the values
9x2 + 16y2 = 162 + 24 × 4
By further calculation
= 256 + 96
= 352
5. If x + y = 8 and x – y = 2, find the value of 2x2 + 2y2.
Solution:
We know that
2 (x2 + y2) = (x + y)2 + (x – y)2
It is given that
x + y = 8 and x – y = 2
Substituting the values
2x2 + 2y2 = 82 + 22
By further calculation
= 64 + 4
= 68
6. If a2 + b2 = 13 and ab = 6, find
(i) a + b
(ii) a – b
Solution:
(i) We know that
(a + b)2 = a2 + b2 + 2ab
Substituting the values
= 13 + 2 × 6
So we get
= 13 + 12
= 25
Here
a + b = ± √25 = ± 5
(ii) We know that
(a – b)2 = a2 + b2 – 2ab
Substituting the values
= 13 – 2 × 6
So we get
= 13 – 12
= 1
Here
a – b = ± √1 = ± 1
7. If a + b = 4 and ab = -12, find
(i) a – b
(ii) a2 – b2.
Solution:
(i) We know that
(a – b)2 = a2 + b2 – 2ab
It can be written as
(a – b)2 = a2 + b2 + 2ab – 4ab
(a – b)2 = (a + b)2 – 4ab
It is given that
a + b = 4 and ab = – 12
Substituting the values
(a – b)2 = 42 – 4 (-12)
By further calculation
(a – b)2 = 16 + 48 = 64
So we get
(a – b) = ± √64 = ± 8
(ii) We know that
a2 – b2 = (a + b) (a – b)
Substituting the values
a2 – b2 = 4 × ±8
a2 – b2 = ± 32
8. If p – q = 9 and pq = 36, evaluate
(i) p + q
(ii) p2 – q2.
Solution:
(i) We know that
(p + q)2 = p2 + q2 + 2pq
It can be written as
(p + q)2 = p2 + q2 – 2pq + 4pq
(p + q)2 = (p – q)2 + 4pq
It is given that
p – q = 9 and pq = 36
Substituting the values
(p + q)2 = 92 + 4 × 36
By further calculation
(p + q)2 = 81 + 144 = 225
So we get
p + q = ± √225 = ± 15
(ii) We know that
p2 – q2 = (p – q) (p + q)
Substituting the values
p2 – q2 = 9 ×±15
p2 – q2 = ± 135
9. If x + y = 6 and x – y = 4, find
(i) x2 + y2
(ii) xy
Solution:
We know that
(x + y)2 – (x – y)2 = 4xy
Substituting the values
62 – 42 = 4xy
By further calculation
36 – 16 = 4xy
20 = 4xy
4xy = 20
So we get
xy = 20/4 = 5
(i) x2 + y2 = (x + y)2 – 2xy
Substituting the values
= 62 – 2 × 5
By further calculation
= 36 – 10
= 26
(ii) xy = 5
10. If x – 3 = 1/x, find the value of x2 + 1/x2.
Solution:
It is given that
x – 3 = 1/x
We can write it as
x – 1/x = 3
Here
(x – 1/x)2 = x2 + 1/x2 – 2
So we get
x2 + 1/x2 = (x – 1/x)2 + 2
Substituting the values
x2 + 1/x2 = 32 + 2
By further calculation
= 9 + 2
= 11
11. If x + y = 8 and xy = 3 ¾, find the values of
(i) x – y
(ii) 3 (x2 + y2)
(iii) 5 (x2 + y2) + 4 (x – y).
Solution:
(i) We know that
(x – y)2 = x2 + y2 – 2xy
It can be written as
(x – y)2 = x2 + y2 + 2xy – 4xy
(x – y)2 = (x + y)2 – 4xy
It is given that
x + y = 8 and xy = 3 ¾ = 15/4
Substituting the values
(x – y)2 = 82 – 4 × 15/4
So we get
(x – y)2 = 65 – 15 = 49
x – y = ± √49 = ± 7
(ii) We know that
(x + y)2 = x2 + y2 + 2xy
We can write it as
x2 + y2 = (x + y)2 – 2xy
It is given that
x + y = 8 and xy = 3 ¾ = 15/4
Substituting the values
x2 + y2 = 82 – 2 × 15/4
So we get
x2 + y2 = 64 – 15/2
Taking LCM
x2 + y2 = (128 – 15)/ 2 = 113/2
We get
3 (x2 + y2) = 3 × 113/2 = 339/2 = 169 ½
(iii) We know that
5 (x2 + y2) + 4 (x – y) = 5 × 113/2 + 4 × ± 7
By further calculation
= 565/2 ± 28
We can write it as
= 565/2 + 28 or 565/2 – 28
= 621/2 or 509/2
It can be written as
= 310 ½ or 254 ½
12. If x2 + y2 = 34 and xy = 10 ½, find the value of 2 (x + y)2 + (x – y)2.
Solution:
It is given that
x2 + y2 = 34 and xy = 10 ½ = 21/2
We know that
(x + y)2 = x2 + y2 + 2xy
Substituting the values
(x + y)2 = 34 + 2 (21/2)
So we get
(x + y)2 = 55 ….. (1)
We know that
(x – y)2 = x2 + y2 – 2xy
Substituting the values
(x – y)2 = 34 – 2 (21/2)
So we get
(x – y)2 = 34 – 21 = 13 ….. (2)
Using both the equations
2 (x + y)2 + (x – y)2 = 2 × 55 + 13 = 123
13. If a – b = 3 and ab = 4, find a3 – b3.
Solution:
We know that
a3 – b3 = (a – b)3 + 3ab (a + b)
Substituting the values
a3 – b3 = 33 + 3 × 4 × 3
By further calculation
a3 – b3 = 27 + 36 = 63
14. If 2a – 3b = 3 and ab = 2, find the value of 8a3 – 27b3.
Solution:
We know that
8a3 – 27b3 = (2a)3 – (3b)3
According to the formula
= (2a – 3b)3 + 3 × 2a × 3b (2a – 3b)
By further simplification
= (2a – 3b)3 + 18ab (2a – 3b)
Substituting the values
= 33 + 18 × 2 × 3
By further calculation
= 27 + 108
= 135
15. If x + 1/x = 4, find the values of
(i) x2 + 1/x2
(ii) x4 + 1/x4
(iii) x3 + 1/x3
(iv) x – 1/x.
Solution:
(i) We know that
(x + 1/x)2 = x2 + 1/x2 + 2
It can be written as
x2 + 1/x2 = (x + 1/x)2 – 2
Substituting the values
= 42 – 2
= 16 – 2
= 14
(ii) We know that
(x2 + 1/x2)2 = x4 + 1/x4 + 2
It can be written as
x4 + 1/x4 = (x2 + 1/x2)2 – 2
Substituting the values
= 142 – 2
= 196 – 2
= 194
(iii) We know that
x3 + 1/x3 = (x + 1/x)3 – 3x (1/x) (x + 1/x)
It can be written as
(x + 1/x)3 – 3(x + 1/x) = 43 – 3 × 4
By further calculation
= 64 – 12
= 52
(iv) We know that
(x – 1/x)2 = x2 + 1/x2 – 2
Substituting the values
= 14 – 2
= 12
So we get
x – 1/x = ± 2√3
16. If x – 1/x = 5, find the value of x4 + 1/x4.
Solution:
We know that
(x – 1/x)2 = x2 + 1/x2 – 2
It can be written as
x2 + 1/x2 = (x – 1/x)2 + 2
Substituting the values
x2 + 1/x2 = 52 + 2 = 27
Here
x4 + 1/x4 = (x2 + 1/x2)2 – 2
Substituting the values
x4 + 1/x4 = 272 – 2
So we get
= 729 – 2
= 727
17. If x – 1/x = √5, find the values of
(i) x2 + 1/x2
(ii) x + 1/x
(iii) x3 + 1/x3
Solution:
(i) x2 + 1/x2 = (x – 1/x)2 + 2
Substituting the values
= (√5)2 + 2
= 5 + 2
= 7
(ii) (x + 1/x)2 = x2 + 1/x2 + 2
Substituting the values
= 7 + 2
= 9
Here
(x + 1/x)2 = 9
So we get
(x + 1/x) = ± √9 = ± 3
(iii) x3 + 1/x3 = (x + 1/x)3 – 3x (1/x) (x + 1/x)
Substituting the values
= (± 3)3 – 3 (± 3)
By further calculation
= (± 27) – (± 9)
= ± 18
18. If x + 1/x = 6, find
(i) x – 1/x
(ii) x2 – 1/x2.
Solution:
(i) We know that
(x – 1/x)2 = x2 + 1/x2 – 2
It can be written as
(x – 1/x)2 = x2 + 1/x2 + 2 – 4
(x – 1/x)2 = (x + 1/x)2 – 4
Substituting the values
(x – 1/x)2 = 62 – 4 = 32
So we get
x – 1/x = ± √32 = ± 4√2
(ii) We know that
x2 – 1/x2 = (x – 1/x) (x + 1/x)
Substituting the values
x2 – 1/x2 = (± 4√2) (6) = ± 24 √2
19. If x + 1/x = 2, prove that x2 + 1/x2 = x3 + 1/x3 = x4 + 1/x4.
Solution:
We know that
x2 + 1/x2 = (x + 1/x) – 2
Substituting the values
x2 + 1/x2 = 22 – 2
So we get
x2 + 1/x2 = 4 – 2 = 2 …. (1)
x3 + 1/x3 = (x + 1/x)3 – 3 (x + 1/x)
Substituting the values
x3 + 1/x3 = 23 – 3 × 2
So we get
x3 + 1/x3 = 8 – 6 = 2 …… (2)
x4 + 1/x4 = (x2 + 1/x2)2 – 2
Substituting the values
x4 + 1/x4 = 22 – 2
So we get
x4 + 1/x4 = 4 – 2 = 2 …. (3)
From equation (1), (2) and (3)
x2 + 1/x2 = x3 + 1/x3 = x4 + 1/x4
Hence, it is proved.
20. If x – 2/x = 3, find the value of x3 – 8/x3.
Solution:
We know that
(x – 2/x)3 = x3 – 8/x3 – 3 (x) (2/x) (x – 2/x)
By further simplification
(x – 2/x)3 = x3 – 8/x3 – 6 (x – 2/x)
It can be written as
x3 – 8/x3 = (x – 2/x)3 + 6 (x – 2/x)
Substituting the values
x3 – 8/x3 = 33 + 6 × 3
By further calculation
x3 – 8/x3 = 27 + 18 = 45
21. If a + 2b = 5, prove that a3 + 8b3 + 30ab = 125.
Solution:
We know that
(a + 2b)3 = a3 + 8b3 + 3 (a) (2b) (a + 2b)
Substituting the values
53 = a3 + 8b3 + 6ab (5)
By further calculation
125 = a3 + 8b3 + 30ab
Therefore, a3 + 8b3 + 30ab = 125.
22. If a + 1/a = p, prove that a3 + 1/a3 = p (p2 – 3).
Solution:
We know that
a3 + 1/a3 = (a + 1/a)3 – 3a (1/a) (a + 1/a)
Substituting the values
a3 + 1/a3 = p3 – 3p
Taking p as common
a3 + 1/a3 = p (p2 – 3)
Therefore, it is proved.
23. If x2 + 1/x2 = 27, find the value of x – 1/x.
Solution:
We know that
(x – 1/x)2 = x2 + 1/x2 – 2
Substituting the values
(x – 1/x)2 = 27 – 2 = 25
So we get
x – 1/x = ± √25 = ± 5
24. If x2 + 1/x2 = 27, find the value of 3x3 + 5x – 3/x3 – 5/x.
Solution:
We know that
(x – 1/x)2 = x2 + 1/x2 – 2
Substituting the values
(x – 1/x)2 = 27 – 2 = 25
So we get
x – 1/x = ± √25 = ± 5
Here
3x3 + 5x – 3/x3 – 5/x = 3 (x3 – 1/x3) + 5 (x – 1/x)
It can be written as
= 3 [(x – 1/x)3 + 3 (x – 1/x)] + 5 (x – 1/x)
Substituting the values
= 3 [(± 5)3 + 3 (± 5)] + 5 (± 5)
By further calculation
= 3 [(± 125) + (± 15)] + (± 25)
So we get
= (± 375) + (± 45) + (± 25)
= ± 445
25. If x2 + 1/25x2 = 8 3/5, find x + 1/5x.
Solution:
We know that
(x + 1/5x)2 = x2 + 1/25x2 + 2x (1/5x)
It can be written as
(x + 1/5x)2 = x2 + 1/25x2 + 2/5
Substituting the values
(x + 1/5x)2 = 8 3/5 + 2/5
(x + 1/5x)2 = 43/5 + 2/5
So we get
(x + 1/5x)2 = 45/5 = 9
Here
x + 1/5x = ± √9 = ± 3
26. If x2 + 1/4x2 = 8, find x3 + 1/8x3.
Solution:
We know that
(x + 1/2x)2 = x2 + (1/2x)2 + 2x (1/2x)
It can be written as
(x + 1/2x)2 = x2 + 1/4x2 + 1
Substituting the values
(x + 1/2x)2 = 8 + 1 = 9
So we get
x + 1/2x = ± √9 = ± 3
Here
x3 + 1/8x3 = x3 + (1/2x)3
We know that
x3 + 1/8x3 = (x + 1/2x)3 – 3x (1/2x) (x + 1/2x)
Substituting the values
x3 + 1/8x3 = (± 3)3 – 3/2 (± 3)
By further calculation
x3 + 1/8x3 = ± (27 – 9/2)
Taking LCM
x3 + 1/8x3 = ± (54 – 9)/ 2
x3 + 1/8x3 = ± 45/2 = ± 22 ½
Therefore, x3 + 1/8x3 = ± 22 ½.
27. If a2 – 3a + 1 = 0, find
(i) a2 + 1/a2
(ii) a3 + 1/a3.
Solution:
It is given that
a2 – 3a + 1 = 0
By dividing each term by a
a + 1/a = 3
(i) We know that
(a + 1/a)2 = a2 + 1/a2 + 2
It can be written as
a2 + 1/a2 = (a + 1/a)2 – 2
Substituting the values
= 32 – 2
= 9 – 2
= 7
(ii) We know that
(a + 1/a)3 = a3 + 1/a3 + 3 (a + 1/a)
It can be written as
a3 + 1/a3 = (a + 1/a)3 – 3 (a + 1/a)
Substituting the values
= 33 – 3 (3)
= 27 – 9
= 18
28. If a = 1/ (a – 5), find
(i) a – 1/a
(ii) a + 1/a
(iii) a2 – 1/a2.
Solution:
It is given that
a = 1/ (a – 5)
We can write it as
a2 – 5a – 1 = 0
Now divide each term by a
a – 5 – 1/a = 0
So we get
a – 1/a = 5
(i) a – 1/a = 5
(ii) We know that
(a + 1/a)2 = (a – 1/a)2 + 4
Substituting the values
(a + 1/a)2 = 52 + 4
So we get
(a + 1/a)2 = 25 + 4 = 29
a + 1/a = ± √29
(ii) We know that
a2 – 1/a2 = (a + 1/a) (a – 1/a)
Substituting the values
a2 – 1/a2 = ± √29 × 5
a2 – 1/a2 = ± 5√29
29. If (x + 1/x)2 = 3, find x3 + 1/x3.
Solution:
It is given that
(x + 1/x)2 = 3
(x + 1/x) = ± √3
We know that
x3 + 1/x3 = (x + 1/x)3 – 3 (x + 1/x)
Substituting the values
x3 + 1/x3 = (± √3)3 – 3 (± √3)
By further calculation
x3 + 1/x3 = (± 3√3) – (± 3√3) = 0
30. If x = 5 – 2√6, find the value of √x + 1/√x.
Solution:
It is given that
x = 5 – 2√6
We can write it as

= 5 + 2√6
Here
x + 1/x = 5 – 2√6 + 5 + 2√6 = 10
So we get
(√x + 1/√x)2 = x + 1/x + 2
Substituting the values
= 10 + 2
= 12
31. If a + b + c = 12 and ab + bc + ca = 22, find a2 + b2 + c2.
Solution:
We know that
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
We can write it as
a2 + b2 + c2 = (a + b + c)2 – 2 (ab + bc + ca)
Substituting the values
a2 + b2 + c2 = 122 – 2 (22)
By further calculation
a2 + b2 + c2 = 144 – 44 = 100
32. If a + b + c = 12 and a2 + b2 + c2 = 100, find ab + bc + ca.
Solution:
We know that
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
It can be written as
2ab + 2bc + 2ca = (a + b + c)2 – (a2 + b2 + c2)
Taking out 2 as common
2 (ab + bc + ca) = 122 – 100 = 144 – 100 = 44
By further calculation
ab + bc + ca = 44/2 = 22
33. If a2 + b2 + c2 = 125 and ab + bc + ca = 50, find a + b + c.
Solution:
We know that
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
Substituting the values
(a + b + c)2 = 125 + 2 (50)
By further calculation
(a + b + c)2 = 125 + 100 = 225
So we get
a + b + c = ± √225 = ± 15
34. If a + b – c = 5 and a2 + b2 + c2 = 29, find the value of ab – bc – ca.
Solution:
It is given that
a + b – c = 5
By squaring on both sides
(a + b – c)2 = 52
Expanding using formula
a2 + b2 + c2 + 2ab – 2bc – 2ca = 25
Substituting the values and taking 2 as common
29 + 2 (ab – bc – ca) = 25
By further calculation
2 (ab – bc – ca) = 25 – 29 = – 4
So we get
ab – bc – ca = – 4/2 = – 2
Therefore, ab – bc – ca = – 2.
35. If a – b = 7 and a2 + b2 = 85, then find the value of a3 – b3.
Solution:
We know that
(a – b)2 = a2 + b2 – 2ab
Substituting the values
72 = 85 – 2ab
By further calculation
49 = 85 – 2ab
So we get
2ab = 85 – 49 = 36
Dividing by 2
ab = 36/2 = 18
Here
a3 – b3 = (a – b) (a2 + b2 + ab)
Substituting the values
a3 – b3 = 7 (85 + 18)
By further calculation
a3 – b3 = 7 × 103
So we get
a3 – b3 = 721
36. If the number x is 3 less than the number y and the sum of the squares of x and y is 29, find the product of x and y.
Solution:
It is given that
x = y – 3 and x2 + y2 = 29
It can be written as
x – y = – 3
By squaring on both sides
(x – y)2 = (-3)2
Expanding using formula
x2 + y2 – 2xy = 9
Substituting the values
29 – 2xy = 9
By further calculation
-2xy = 9 – 29 = – 20
Dividing by 2
xy = – 20/-2 = 10
So we get
xy = 10
37. If the sum and the product of two numbers are 8 and 15 respectively, find the sum of their cubes.
Solution:
Consider x and y as the two numbers
x + y = 8 and xy = 15
By cubing on both sides
(x + y)3 = 83
Expanding using formula
x3 + y3 + 3xy (x + y) = 512
Substituting the values
x3 + y3 + 3 × 15 × 8 = 512
By further calculation
x3 + y3 + 360 = 512
So we get
x3 + y3 = 512 – 360 = 152
Chapter Test
1. Find the expansions of the following :
(i) (2x + 3y + 5) (2x + 3y – 5)
(ii) (6 – 4a -7b)2
(iii) (7 – 3xy)3
(iv) (x + y + 2)3
Solution:
(i) (2x + 3y + 5) (2x + 3y – 5)
Let us simplify the expression, we get
(2x + 3y + 5) (2x + 3y – 5) = [(2x + 3y) + 5] [(2x – 3y) – 5]
By using the formula, (a)2 – (b)2 = [(a + b) (a – b)]
= (2x + 3y)2 – (5)2
= (2x)2 + (3y) 2 + 2 × 2x × 3y – 5 × 5
= 4x2 + 9y2 + 12xy – 25
(ii) (6 – 4a – 7 b)2
Let us simplify the expression, we get
(6 – 4a – 7 b)2 = [ 6 + (- 4a) + (-7b)]2
= (6)2 + (- 4a)2 + (- 7b)2 + 2 (6) (- 4a) + 2 (- 4a) (-7b) + 2 (-7b) (6)
= 36 + 16a2 + 49b2 – 48a + 56ab – 84b
(iii) (7 – 3xy)3
Let us simplify the expression
By using the formula, we get
(7 – 3xy)3 = (7)3 – (3xy)3 – 3 (7) (3xy) (7 – 3xy)
= 343 – 27x3y3 – 63xy (7 – 3xy)
= 343 – 27x3y3 – 441xy + 189x2y2
(iv) (x + y + 2)3
Let us simplify the expression
By using the formula, we get
(x + y + 2 )3 = [(x + y) + 2]3
= (x + y)3 + (2)3 + 3 (x + y) (2) (x + y + 2)
= x3 + y3 + 3x2y + 3xy2 + 8 + 6 (x + y) [(x + y) + 2]
= x3 + y3 + 3x2y + 3xy2 + 8 + 6 (x + y)2 +12(x + y)
= x3 + y3 + 3x2y + 3xy2 + 8 + 6 (x2 + y2 + 2xy) + 12x + 12y = x3 + y3 + 3x2y + 3xy2 + 8 + 6x2 + 6y2 + 12xy + 12x + 12y
= x3 + y3 + 3x2y + 3xy2 + 8 + 6x2 + 6y2 + 12x + 12y + 12xy
2. Simplify: (x – 2) (x + 2) (x2 + 4) (x4 + 16)
Solution:
Let us simplify the expression, we get
(x – 2) (x + 2) (x4 + 4) (x4 +16) = (x2 – 4) (x4 + 4) (x4 + 16)
= [(x2)2 – (4)2] (x4 + 16)
= (x4 – 16) (x4 + 16)
= (x4)2 – (16)2
= x8 – 256
3. Evaluate 1002 × 998 by using a special product.
Solution:
Let us simplify the expression, we get
1002 × 998 = (1000 + 2) (1000 – 2)
= (1000)2 – (2)2
= 1000000 – 4
= 999996
4. If a + 2b + 3c = 0, Prove that a3 + 8b3 + 27c3 = 18 abc
Solution:
Given:
a + 2b + 3c = 0, a + 2b = – 3c
Let us cube on both sides, and we get
(a + 2b)3 = (-3c)3
a3 + (2b)3 + 3(a) (2b) (a + 2b) = -27c3
a3 + 8b3 + 6ab (– 3c) = – 27c3
a3 + 8b3 – 18abc = -27c3
a3 + 8b3 + 27c3 = 18abc
Hence proved.
5. If 2x = 3y – 5, then find the value of 8x3 – 27y3 + 90xy + 125.
Solution:
Given:
2x = 3y – 5
2x – 3y = -5
Now, let us cube on both sides, we get
(2x – 3y)3 = (-5)3
(2x)3 – (3y)3 – 3 × 2x × 3y (2x – 3y) = -125
8x3 – 27y3 – 18xy (2x – 3y) = -125
Now, substitute the value of 2x – 3y = -5
8x3 – 27y3 – 18xy (-5) = -125
8x3 – 27y3 + 90xy = -125
8x3 – 27y3 + 90xy + 125 = 0
6. If a2 – 1/a2 = 5, evaluate a4 + 1/a4
Solution:
It is given that,
a2 – 1/a2 = 5
So,
By using the formula (a + b)2
[a2 – 1/a2]2 = a4 + 1/a4 – 2 [a2 – 1/a2]2 + 2 = a4 + 1/a4Substitute the value of a2 – 1/a2 = 5, we get
52 + 2 = a4 + 1/a4
a4 + 1/a4 = 25 + 2
= 27
7. If a + 1/a = p and a – 1/a = q, Find the relation between p and q.
Solution:
It is given that,
a + 1/a = p and a – 1/a = q
so,
(a + 1/a)2 – (a – 1/a)2 = 4(a) (1/a)
= 4
By substituting the values, we get
p2 – q2 = 4
Hence the relation between p and q is that p2 – q2 = 4.
8. If (a2 + 1)/a = 4, find the value of 2a3 + 2/a3
Solution:
It is given that,
(a2 + 1)/a = 4
a2/a + 1/a = 4
a + 1/a = 4
So by multiplying the expression by 2a, we get
2a3 + 2/a3 = 2[a3 + 1/a3]
= 2 [(a + 1/a)3 – 3 (a) (1/a) (a + 1/a)]
= 2 [(4)3 – 3(4)]
= 2 [64 – 12]
= 2 (52)
= 104
9. If x = 1/(4 – x), find the value of
(i) x + 1/x
(ii) x3 + 1/x3
(iii) x6 + 1/x6
Solution:
It is given that,
x = 1/(4 – x)
So,
(i) x(4 – x) = 1
4x – x2 = 1
Now let us divide both sides by x, we get
4 – x = 1/x
4 = 1/x + x
1/x + x = 4
1/x + x = 4
(ii) x3 + 1/x3 = (x + 1/x)2 – 3(x + 1/x)
By substituting the values, we get
= (4)3 – 3(4)
= 64 – 12
= 52
(iii) x6 + 1/x6 = (x3 + 1/x3)2 – 2
= (52)2 – 2
= 2704 – 2
= 2702
10. If x – 1/x = 3 + 2√2, find the value of ¼ (x3 – 1/x3)
Solution:
It is given that,
x – 1/x = 3 + 2√2
So,
x3 – 1/x3 = (x – 1/x)3 + 3(x – 1/x)
= (3 + 2√2)3 + 3(3 + 2√2)
By using the formula, (a+b)3 = a3 + b3 + 3ab (a + b)
= (3)3 + (2√2)3 + 3 (3) (2√2) (3 + 2√2) + 3(3 + 2√2)
= 27 + 16√2 + 54√2 + 72 + 9 + 6√2
= 108 + 76√2
Hence,
¼ (x3 – 1/x3) = ¼ (108 + 76√2)
= 27 + 19√2
11. If x + 1/x = 3 1/3, find the value of x3 – 1/x3
Solution:
It is given that,
x + 1/x = 3 1/3
we know that,
(x – 1/x)2 = x2 + 1/x2 – 2
= x2 + 1/x2 + 2 – 4
= (x + 1/x)2 – 4
But x + 1/x = 3 1/3 = 10/3
So,
(x – 1/x)2 = (10/3)2 – 4
= 100/9 – 4
= (100 – 36)/9
= 64/9
x – 1/x = √(64/9)
= 8/3
Now,
x3 – 1/x3 = (x – 1/x)3 + 3 (x) (1/x) (x – 1/x)
= (8/3)3 + 3 (8/3)
= ((512/27) + 8)
= 728/27
= 26 26/27
12. If x = 2 – √3, then find the value of x3 – 1/x3
Solution:
It is given that,
x = 2 – √3
so,
1/x = 1/(2 – √3)
By rationalizing the denominator, we get
= [1(2 + √3)] / [(2 – √3) (2 + √3)]
= [(2 + √3)] / [(22) – (√3)2]
= [(2 + √3)] / [4 – 3]
= 2 + √3
Now,
x – 1/x = 2 – √3 – 2 – √3
= – 2√3
Let us cube on both sides, we get
(x – 1/x)3 = (-2√3)3
x3 – 1/x3 – 3 (x) (1/x) (x – 1/x) = 24√3
x3 – 1/x3 – 3(-2√3) = -24√3
x3 – 1/x3 + 6√3 = -24√3
x3 – 1/x3 = -24√3 – 6√3
= -30√3
Hence,
x3 – 1/x3 = -30√3
13. If the sum of two numbers is 11 and sum of their cubes is 737, find the sum of their squares.
Solution:
Let us consider x and y to be two numbers
Then,
x + y = 11
x3 + y3 = 735 and x2 + y2 =?
Now,
x + y = 11
Let us cube on both sides,
(x + y)3 = (11)3
x3 + y3 + 3xy (x + y) = 1331
737 + 3x × 11 = 1331
33xy = 1331 – 737
= 594
xy = 594/33
xy = 8
We know that, x + y = 11
By squaring on both sides, we get
(x + y)2 = (11)2
x2 + y2 + 2xy = 121 2 x2 + y2 + 2 × 18 = 121
x2 + y2 + 36 = 121
x2 + y2 = 121 – 36
= 85
Hence the sum of the squares = 85
14. If a – b = 7 and a3 – b3 = 133, find:
(i) ab
(ii) a2 + b2
Solution:
It is given that,
a – b = 7
let us cube on both sides, we get
(i) (a – b)3 = (7)3
a3 + b3 – 3ab (a – b) = 343
133 – 3ab × 7 = 343
133 – 21ab = 343
– 21ab = 343 – 133 21ab
= 210
ab = -210/21
ab = -10
(ii) a2 + b2
Again a – b = 7
Let us square on both sides, we get
(a – b)2 = (7)2
a2 + b2 – 2ab = 49
a2 + b2 – 2 × (- 10) = 49
a2 + b2 + 20 = 49
a2 + b2 = 49 – 20
= 29
Hence, a2 + b2 = 29
15. Find the coefficient of x2 expansion of (x2 + x + 1)2 + (x2 – x + 1)2
Solution:
Given:
The expression, (x2 + x + 1)2 + (x2 – x + 1)2
(x2 + x + 1)2 + (x2 – x + 1)2 = [((x2 + 1) + x)2 + [(x2 + 1) – x)2]
= (x2 + 1)2 + x2 + 2 (x2 + 1) (x) + (x2 + 1)2 + x2 – 2 (x2 + 1) (x)
= (x2)2 + (1)2 + 2 × x2 × 1 + x2 + (x2)2 + 1 + 2 × x2 + 1 + x2
= x4 + 1 + 2x2 + x2 + x4 + 1 + 2x2 + x2
= 2x4 + 6x2 + 2
∴ Coefficient of x2 is 6.













































Good