Alternating Current formulae for NEET

Alternating current is a current that changes its magnitude and polarity at regular interval of time. If the current maintains its direction constant it is called direct current.

AC voltage, v = V₀sinωt

AC current, i = I₀sinωt

Capacitive Reactance V₀/I₀ = 1/ωC = X_c

RMS voltage, V_rms = V₀/√2

RMS current, I_rms = I₀/√2

Inductive Reactance  V₀/I₀ = ωL = X_L

Phase angle of an RLC series circuit Φ = tan^-1 (X_L – X_C)/R

AC version of Ohm’s law, I₀ = V₀/Z

RLC series circuit Impedance , 

Average power associated with circuit element, P_avc = (1/2)I₀V₀cos Φ

Resonant angular frequency of the circuit, ω₀ = √1/LC

Root Mean Square: The Root mean square of a function from T1 to T2 is given by

Power Consumed or Supplied in AC circuit

The average power consumed in a cycle

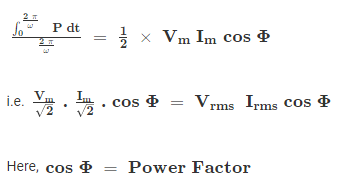
Purely Resistive Circuit: In a purely resistive circuit, the power is dissipated by the resistance and phase of both voltage and current remains the same.

P = V_rmsI_rms cosΦ = V_rms²/R

Pure Inductive Circuit: In a purely inductive circuit current lags the voltage by 90⁰

i = i_m sin(ωt- π/2)

Purely Conductive Circuit: In a purely inductive circuit, the current flowing through the capacitor leads the voltage by 90⁰.

I = {V_m/(1/ωC)}cosωt

I = (V_m/X_c)cosωt

I = I_mcosωt

I = I_msin(ωt + π/2)

Recommended Video:

Electric Current and Electrical Networks | Ohm’s Law in Scalar form | NEET 2021/2022/2023 | Physics

You might like:

• NEET Physics Syllabus
• How to Score 170 Plus in NEET Physics
• Last Minute Preparation Tips for NEET Physics
• NEET Physics Weightage
• Physics Formulae For NEET
• NEET Physics Important Topics
• NEET Physics MCQs