Heisenberg’s uncertainty principle states that it is impossible to measure or calculate exactly both the position and the momentum of an object. This principle is based on the wave-particle duality of matter. Although Heisenberg’s uncertainty principle can be ignored in the macroscopic world (the uncertainties in the position and velocity of objects with relatively large masses are negligible), it holds significant value in the quantum world. Since atoms and subatomic particles have very small masses, any increase in the accuracy of their positions will be accompanied by an increase in the uncertainty associated with their velocities.
Download Complete Chapter Notes of Structure of Atom
Download Now
Table of Contents
In the field of quantum mechanics, Heisenberg’s uncertainty principle is a fundamental theory that explains why it is impossible to measure more than one quantum variable simultaneously. Another implication of the uncertainty principle is that it is impossible to accurately measure the energy of a system in some finite amount of time.
Why Is It Impossible to Measure Both Position and Momentum Simultaneously?In order to illustrate Heisenberg’s uncertainty principle, consider an example where the position of an electron is measured. In order to measure the position of an object, a photon must collide with it and return to the measuring device. Since photons hold some finite momentum, a transfer of momenta will occur when the photon collides with the electron. This transfer of momenta will cause the momentum of the electron to increase. Thus, any attempt at measuring the position of a particle will increase the uncertainty in the value of its momentum. Applying the same example to a macroscopic object (say a basketball), it can be understood that Heisenberg’s uncertainty principle has a negligible impact on measurements in the macroscopic world. While measuring the position of a basketball, there will still be a transfer of momentum from the photons to the ball. However, the mass of the photon is much smaller than the mass of the ball. Therefore, any momentum imparted by the photon to the ball can be neglected. |
Heisenberg’s uncertainty principle imposes a restriction on the accuracy of simultaneous measurement of position and momentum. The more precise our measurement of position is, the less accurate will be our momentum measurement and vice-versa. The physical origin of Heisenberg’s uncertainty principle is with the quantum system. Determination of position by performing a measurement on the system disturbs it sufficiently to make the determination of q imprecise and vice-versa. We will learn about the principle in detail below.
What Is Heisenberg’s Uncertainty Principle?
Heisenberg’s uncertainty principle states that for particles exhibiting both particle and wave nature, it will not be possible to accurately determine both the position and velocity at the same time. The principle is named after German physicist Werner Heisenberg, who proposed the uncertainty principle in the year 1927. This principle was formulated when Heisenberg was trying to build an intuitive model of quantum physics. He discovered that there were certain fundamental factors that limited our actions in knowing certain quantities.
This principle basically highlights that simultaneous measurement of position and the velocity or momentum of microscopic matter waves will have an error such that the product of the error in measurement of position and momentum is equal or more than an integral multiple of a constant.
Origin of the Uncertainty Principle
One of the crucial points for the genesis of the uncertainty principle is solely due to the dual nature of a wave-particle. Every particle is said to have a wave nature, and the probability of finding particles is maximum, where the waveforms are the greatest. If the particle has greater undulation, the wavelength becomes more indistinct or vague. However, we are able to determine the momentum of the particle. From what we have learnt so far, we can say that the particles that have definite positions will have no fixed velocity. On the other hand, a particle with a well-defined wavelength will show a definitive or precise velocity. All in all, if we get an accurate reading of one quantity, it will only lead to large uncertainty in the measurement of the other.
Heisenberg Uncertainty Principle Formula and Application
If ∆x is the error in position measurement and ∆p is the error in the measurement of momentum, then
Since momentum, p = mv, Heisenberg’s uncertainty principle formula can be alternatively written as,
Where, ∆V is the error in the measurement of velocity, and assuming mass remains constant during the experiment,
Accurate measurement of position or momentum automatically indicates larger uncertainty (error) in the measurement of the other quantity.
Applying the Heisenberg principle to an electron in an orbit of an atom, with h = 6.626 ×10-34Js and m= 9.11 ×10-31Kg,
If the position of the electron is measured accurately to its size (10-10m), then the error in the measurement of its velocity will be equal to or larger than 106m or 1000 km.
Heisenberg’s principle applies to only dual-natured microscopic particles and not to macroscopic particles whose wave nature is minimal.
Also Read: de Broglie Equation
Explaining Heisenberg Uncertainty Principle with an Example
Electromagnetic radiations and microscopic matter waves exhibit a dual nature of mass/momentum and wave character. The position and velocity/momentum of macroscopic matter waves can be determined accurately and simultaneously. For example, the location and speed of a moving car can be determined simultaneously with minimum error. But, in microscopic particles, it will not be possible to fix the position and measure the velocity/momentum of the particle simultaneously.
An electron in an atom has a mass of 9.91 × 10-31 kg. Naked eyes cannot see such small particles. A powerful light may collide with the electron and illuminate it. Illumination helps in identifying and measuring the position of the electron. The collision of the powerful light source, while helping in identification, increases the momentum of the electron and makes it move away from the initial position. Thus, when fixing the position, the velocity/momentum of the particle would have changed from the original value. Hence, when the position is exact, the error occurs in measuring velocity or momentum. In the same way, the measurement of momentum, accurately, will change the position.
Hence, at any point in time, either position or momentum can only be measured accurately.
Simultaneous measurement of both of them will have an error in both position and momentum. Heisenberg quantified the error in the measurement of both position and momentum simultaneously.
Heisenberg’s γ-ray Microscope
A striking thought experiment illustrating the uncertainty principle is Bohr’s/Heisenberg’s Gamma-ray microscope. To observe a particle, say an electron, we shine it with the light ray of wavelength λ and collect the Compton scattered light in a microscope objective whose diameter subtends an angle θ with the electron, as shown in the figure below
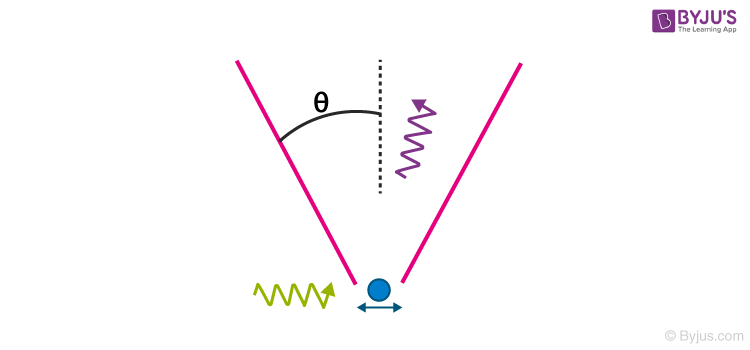
The precision with which the electron can be located, Delta x, is defined by the resolving power of the microscope,
It appears that by making λ small, we choose γ-ray, and by making sin θ large, Delta x can be made as small as desired. But, according to the uncertainty principle, we can do so only at the expense of our knowledge of the x-component of electron momentum.
In order to record the Compton scattered photon by the microscope, the photon must stay in the cone of angle θ, and hence its x-component of the momentum can vary within ±(h/λ) sin θ. This implies that the magnitude of the recoil momentum of the electron is uncertain by
The product of the uncertainty yields,
Is Heisenberg’s Uncertainty Principle Noticeable in All Matter Waves?
Heisenberg’s principle is applicable to all matter waves. The measurement error of any two conjugate properties, whose dimensions happen to be joule sec, like position-momentum, the time-energy will be guided by Heisenberg’s value.
But, it will be noticeable and of significance only for small particles like an electron with very low mass. A bigger particle with a heavy mass will show the error to be very small and negligible.
Heisenberg Uncertainty Principle Equations
Heisenberg’s uncertainty principle can be considered as a very precise mathematical statement that describes the nature of quantum systems. As such, we often consider two common equations related to the uncertainty principle, and they are as follows:
Equation 1: ∆X ⋅ ∆p ~ ħ
Equation 2: ∆E ⋅ ∆t ~ ħ
Where,
ħ = value of Planck’s constant divided by 2*pi
∆X = uncertainty in the position
∆p = uncertainty in momentum
∆E = uncertainty in the energy
∆t = uncertainty in time measurement
Solved Numerical Problems on Heisenberg’s Uncertainty Principle
1. If the position of the electron is measured within an accuracy of + 0.002 nm, calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is h / 4pm × 0.05 nm. Is there any problem in defining this value?
a) ∆x = 2×10-12m;
b) Momentum
Error in momentum measurement is 1010 times larger than the actual momentum. The given momentum will not be acceptable.
2. Position of a chloride ion on a material can be determined to a maximum error of 1μm. If the mass of the chloride ion is 5.86 × 10-26kg, what will be the error in its velocity measurement?
∆x = 10-6 m;
3. The lifetime of an excited state of an atom is 3 × 10-3s. What is the minimum uncertainty in its energy in eV?
Time and energy are conjugate pairs with the Js unit. The product of measurement error is given by Heisenberg’s principle.
Assuming a maximum error in the measurement of lifetime equal to that of lifetime = 3 ×10-3s
⸪ 1 Joule = 6.242 × 1018ev,
Uncertainty in the determination of energy of the atom = ∆E
= 1.1 × 10-13
4. A wet ball weighing 10.1gm has a water of 0.1 g on it. The ball is moving with a constant velocity with an uncertainty of momentum of 10-6 kg m/s. What will be the uncertainty in the measurement of the position of the ball, water and electron in the water molecule?
Velocity being constant, uncertainty in the measurement of the momentum is associated with the mass of the matter.
Uncertainty in the momentum of the dry ball = mass ×10-6 = 10×10-3×10-6 Kg m s-1.
Uncertainty in the momentum of the water = mass ×10-6 = 0.1×10-3×10-6 Kg m s-1.
Uncertainty in the momentum of the electron = mass ×10-6 = 9×10-31×10-6 Kg m s-1.
Uncertainty in position measurement is inversely proportional to the uncertainty in momentum.
∆Xb : ∆Xw : ∆Xe
= 108 : 1010 : 1.1 × 1036 or
= 1 : 102 : 1028
5. Determine the minimum uncertainties in the positions of the electron if their speeds are known with a precision of 3.0 × 10−3m/s.
Solution:
Δu = 3.0×10−3m/s
Uncertained momentum Δp = m Δu
Uncertainty in position Δx = ℏ/(2Δp)
For electron
Δp = m Δu
= (9.1×10−31kg × 3.0×10−3)
Δp = 2.73 × 10-33 kg.m/s
Δx = 0.12 m
Frequently Asked Questions on Heisenberg’s Uncertainty Principle
Who was the first to come up with the idea of finding an electron in an orbital?
Heisenberg was the first one to think of or develop this idea.
Is it possible to determine that the electron is located at a certain exact location with 100% accuracy at a fixed time through measurement?
No, we cannot determine.
Which scientists proposed the idea of the uncertainty principle and the concept of the wave nature of matter?
It was Heisenberg and de Broglie.
What violates the Heisenberg uncertainty principle?
If an object travelling through spacetime can loop back in time in a certain way, then its trajectory can allow a pair of its components to be measured with perfect accuracy, violating Heisenberg’s uncertainty principle.

Comments