Centre of Mass of Equilateral Triangle

In geometry, the equilateral triangle is a triangle in which all the three sides are equal. All the internal angles of the equilateral triangle are also equal. The angles are equal to 60⁰.

Test your Knowledge on Equilateral Triangle

Q5

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz

Start Quiz

Congrats!

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

0 out of 0 arewrong

0 out of 0 are correct

0 out of 0 are Unattempted

View Quiz Answers and Analysis

How to Find Centre of Mass of Equilateral Triangle

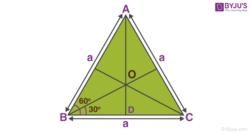
The centre of mass can be calculated by following these steps

Step 1: Find the midpoint of all the three sides of the triangle.

Step 2: Draw a perpendicular from midpoint to the opposite vertex. This perpendicular line is called the median.

Step 3: These three medians meet at a point. This point of intersection of the medians is the centre of mass of the equilateral triangle.

The centre of mass of the equilateral triangle is at a distance of H/3 from the centre of the base of the triangle. H is the height of the triangle. The centroid or the centre of mass divides the median in 2:1 ratio.

Calculation of Distance of the Centre of Mass from the Vertex

Let a be the length of the sides. The internal angle of the equilateral triangle is 60⁰.

Using Pythagoras theorem,

Sin 60⁰ = AD/a

AD = (a√3)/2

Median of the equilateral triangle divides the median by the ratio 2:1

Therefore, OD = (a√3)/6

In triangle OBD

Sin 30⁰ = OD/OB

Sin 30⁰ = ((a√3)/6)/OB

OB = (a√3)/3

For the triangle of side a, the distance from the centre of mass to the vertex is (a√3)/3.