From 2019 onwards National Testing Agency (NTA) will be conducting the JEE (joint entrance examination) every year. JEE exams are competitive exams that are designed to select worthy candidates and provide them admissions into the prestigious IITs in India. However, candidates must work tirelessly with smart work and dedication. A few important chapters and some concepts are highly significant as there is a pattern in which these questions repeat every year. Going through these questions will give you a fair idea about your preparation status and help you to utilize the remaining time before the examination. At this moment, you should focus on selective study and go through the important topics.
Important Questions For Rate Of Reaction
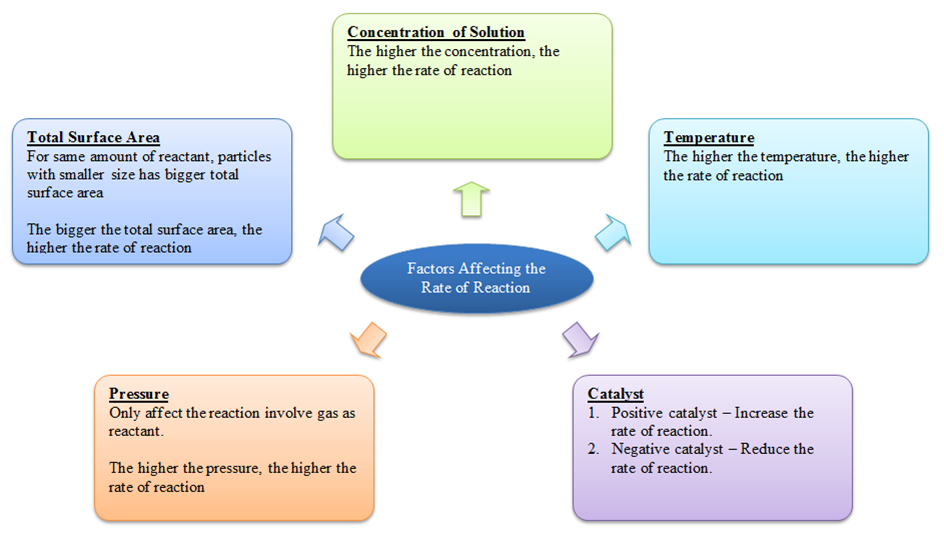
Q.What are the important topics in factors affecting the rate of reaction?
Ans – Following are the concepts that should be studied carefully:
- Nature of the reactants – this includes the physical state of the reactants, the physical size of the reactants, chemical nature of the reactant.
- concentration of reactants
- Effect of temperature
- Catalyst – the presence of a positive catalyst or the presence of a negative catalyst
Q. How to approach a question on factors affecting the rate of reactions?
Q.The rate of a reaction triples when the temperature changes from 20oC to 50oC. Calculate the energy of activation for the reaction (R = 8.314 JK-1mol-1).
Ans: The Arrhenius equation is
Given:
R = 8.314 JK-1 mol–1; T1 = 20 + 273 = 293 K
and T2 = 50 + 273 = 323 K
Subtracting the given values in the Arrhenius equation,
Ea = (2.303 × 8.314 × 323 × 293 × 0.477)/30
= 28811.8 J mol-1
= 28.8118 kJ mol.-1
Books for reference
Refer NCERT textbook for class 12th. This book contains all the details in a very precise manner. A quick view of this can help you to understand the fundamental concepts and their applications. The important points are neatly mentioned in the book making it the most student-friendly book. Some other important reference books include books by O. P. Tandon and P. Bahadur. For more details download BYJU’S the learning app.
Comments