JEE Main 2020 solved Shift 2 Maths paper solutions consist of accurate solutions prepared by subject experts. These step by step solutions help students to understand the problems easily.
Students can understand the question pattern and the difficulty level of questions from each chapter. Practising these solutions will help them to self analyse their preparation. Students can easily download the solutions in PDF format for free.
JEE Advanced 2020 Question Paper
January 9 Shift 2 – Maths
January 9 Shift 2 – Maths
1. If A = {x∈ R∶ |x| <2} and B = {x∈ R∶ |x-2| ≥3} then :
a. A – B = [-1,2]
b. B – A = R-(-2,5)
c. A⋃B = R-(2,5)
d. A∩B = (-2,-1)
A = {x: x ∈ (-2,2)}
B = {x: x ∈ (∞,-1] ⋃ [5, ∞)}
A∩B = {x: x ∈ (-2,-1] }
B – A = {x: x ∈ (∞,-2] ⋃ [5, ∞)}
A – B = {x: x ∈ (-1,2)}
A⋃B = {x: x ∈ (∞,2] ⋃ [5, ∞)}
Answer: (b)
2. If 10 different balls has to be placed in 4 distinct boxes at random, then the probability that two of these boxes contain exactly 2 and 3 balls is :
a. 965/210
b. 945/210
c. 945/211
d. 965/211
Total ways to distribute 10 balls in 4 boxes is = 410
Total ways of placing exactly 2 and 3 balls in any two of these boxes is = 4C2×10C5×(5!/(2!3!))×2×25
P(E) = 945/210
Answer: (b)
3. If x = 2 sin θ – sin 2 θ and y = 2 cos θ – cos 2 θ, θ ∈ [0, 2π], then d2y/dx2 at θ =π is:
a. -3/8
b. 3/4
c. 3/2
d. -3/4
dx/d θ = 2 cos θ -2 cos2 θ
dy/d θ = -2 sin θ + 2 sin2 θ

dy/dx = cot (3 θ/2)
d2y/dx2 = -(3/2) cosec2(3 θ/2)(d θ/dx)
\(\begin{array}{l}\frac{d^{2}y}{dx^{2}}= \left ( -\frac{3}{2}cosec^{2} \: \frac{3\theta}{2} \right )\frac{1}{(2\cos \theta -2\cos 2\theta )}\end{array} \)
(
\(\begin{array}{l}\frac{d^{2}y}{dx^{2}})_{\theta =\pi }= \frac{3}{8}\end{array} \)
Answer : None of the above option satisfies the answer.
4. Let f and g be differentiable functions on R, such that fog is the identity function. If for some a, b ∈ R, g’(a) = 5 and g(a) = b, then f'(b) is equal to :
a. 2/5
b. 5
c. 1
d. 1/5
f(g(x) = x
f’(g(x))g’(x) = 1
put x = a
f’(g(a))g’(a) = 1
f’(b) ×5 = 1
f’(b) = 1/5
Answer: (d)
5. In the expansion of \(\begin{array}{l}\left ( \frac{x}{\cos \theta }+\frac{1}{x\sin \theta } \right )^{16}\end{array} \)
, if l1 is the least value of the term independent of x when (π/8) ≤ θ ≤ (π/4) and l2 is the least value of the term independent of x when (π/16) ≤ θ ≤ (π/8), then the ratio l2 : l1 is equal to :
a. 16:1
b. 8:1
c. 1:8
d. 1:16
\(\begin{array}{l}T_{r+1} =\: ^{16}C_{r}\left ( \frac{x}{\cos \theta } \right )^{16-r}\left ( \frac{1}{x\sin\theta } \right )^{r}\end{array} \)
For term independent of x, 16-2r = 0
⇒ r = 8
T9 =
\(\begin{array}{l}\: ^{16}C_{8}\left ( \frac{1}{\sin \theta \cos \theta } \right )^{8}=\: ^{16}C_{8}2^{8}\left ( \frac{1}{\sin 2\theta } \right )^{8}\end{array} \)
l1 = 16C8 28 at θ = π/4
l2 =
\(\begin{array}{l}^{16}C_{8}\frac{2^{8}}{\left ( \frac{1}{\sqrt{2}} \right )^{8}}= ^{16}C_{8}2^{12} at\: \theta =\frac{\pi }{8}\end{array} \)
l2/l1 = 16:1
Answer: (a)
6. Let a,b ∈R, a ≠ 0, such that the equation, ax2-2bx+5 = 0 has a repeated root α, which is also a root of the equation x2-2bx-10 = 0. If β is the root of this equation, then α2+β2 is equal to:
a. 24
b. 25
c. 26
d. 28
ax2-2bx+5 = 0 has both roots as α
2α = 2b/a
α= b/a
And α2 = 5/a
b2 = 5a (a≠0) ..(i)
α+β = 2b
And αβ = -10
α= b/a is also a root of x2 -2bx-10 = 0
b2 -2ab2-10a2 = 0
b2 = 5a
5a-10a2 -10a2 = 0
a = 1/4
b2 = 5/4
α2 = 20
β2 = 5
α2+β2 = 25
Answer: (b)
7. Let a function f:[0,5] R, be continuous, f(1) = 3 and F be defined as:
F(x) =
\(\begin{array}{l}\int_{1}^{x}t^{2}g(t)dt\end{array} \)
,where \(\begin{array}{l}g(t)=\int_{1}^{t}f(u)du\end{array} \)
Then for the function F, the point x = 1 is
a. a point of inflection.
b. a point of local maxima
c. a point of local minima
d. not a critical point
F'(x) = x2g(x)
Put x = 1
F'(1) = g(1) = 0 ..(i)
Now F’’(x) = 2xg(x) + g’(x)x2
F’’(1) = 2g(1) + g’(1) {∵g’(x) = f(x)}
F’’(1) = f(1) = 3 ..(ii)
From (1) and (2), F(x) has local minimum at x = 1.
Answer: (c)
8. Let [t] denotes the greatest integer ≤ t and \(\begin{array}{l}\lim_{x\to0} x\left [ \frac{4}{x} \right ]= A\end{array} \)
. Then the function, f(x)=[x2] sin πx is discontinuous, when x is equal to
a. √(A+1)
b. √A
c. √(A+5)
d. √(A+21)
f(x)=[x2]sin π x
It is continuous ∀x ∈ Z as sinπx 🡪 as 🡪 Z.
f(x) is discontinuous at points where [x2] is discontinuous i.e. x2∈Z with an exception that f(x) is continuous as x is an integer.
∴ Points of discontinuity for f(x) would be at
x = ±√2, ±√3, ±√5,……
Also, it is given that
\(\begin{array}{l}\lim_{x\to0} x\left [ \frac{4}{x} \right ]= A\end{array} \)
(indeterminate form (0×∞))
\(\begin{array}{l}4-\lim_{x\to0} (\frac{4}{x}) = A\end{array} \)
A = 4
√(A+5) = 3
√(A+1) = √5
√(A+21) =5
√A = 2
Points of discontinuity for f(x) is x = √5
Answer: (a)
9. Let a-2b+c = 1. If f(x) = \(\begin{array}{l}\begin{vmatrix} x+a & x+2&x+1 \\ x+b& x+3 & x+2\\ x+c &x+4 & x+3 \end{vmatrix}\end{array} \)
, then
a. f(-50) = 501
b. f(-50) = -1
c. f(50) = 1
d. f(-50) = -501
Given f(x) =
\(\begin{array}{l}\begin{vmatrix} x+a & x+2&x+1 \\ x+b& x+3 & x+2\\ x+c &x+4 & x+3 \end{vmatrix}\end{array} \)
a -2b+c = 1
Applying R1 🡪 R1 -2R2+ R3
f(x) =
\(\begin{array}{l}\begin{vmatrix} a -2b+c& 0&0 \\ x+b& x+3 & x+2\\ x+c &x+4 & x+3 \end{vmatrix}\end{array} \)
Using a-2b+c = 1
f(x) = (x+3)2 -(x+2)(x+4)
f(x) = 1
f(50) = 1
f(-50) = 1
Answer: (c)
10. Given:
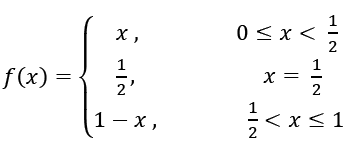
and g(x)= (x− 1/2)2, x ∈ R. Then the area (in sq. units) of the region bounded by the curves y = f(x) and y = g(x) between the lines 2x = 1 to 2x = √3 is :
a. (√3/4) – (1/3)
b. (1/3) + (√3/4)
c. (1/2) + (√3/4)
d. (1/2) – (√ 3/4)

The area between f(x) and g(x) from x = 1/2 to x = √3/2 :

Points of intersection of f(x) and g(x):
1-x = (x- 1/2)2
x = √3/2 ,-√3/2
Required area =
\(\begin{array}{l}\int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}(f(x)-g(x))dx\end{array} \)
=
\(\begin{array}{l}\int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}(1-x-(x-\frac{1}{2})^{2})dx\end{array} \)
=
\(\begin{array}{l}[x-\frac{x^{2}}{2}-\frac{1}{3}(x-\frac{1}{2})^{3}]_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}}\end{array} \)
= (√3/4) – (1/3)
Answer: (a)
11. The following system of linear equations
7x+6y-2z = 0
3x+4y+2z = 0
x-2y-6z = 0, has
a. infinitely many solutions, (x,y,z) satisfying y = 2z
b. infinitely many solutions (x,y,z) satisfying x = 2z
c. no solution
d. only the trivial solution
7x+6y−2z = 0
3x+4y+2z = 0
x−2y−6z = 0
As the system of equations are homogeneous the system is consistent.
\(\begin{array}{l}\begin{vmatrix} 7 & 6&-2 \\ 3&4 & 2\\ 1 & -2 & -6 \end{vmatrix}=0\end{array} \)
⇒ Infinite solutions exist (both trivial and non-trivial solutions)
When y = 2z
Let’s take y = 2, z = 1
When (x,2,1)is substituted in the system of equations
⇒7x+10 = 0 ,3x+10 = 0 , x-10 = 0 (which is not possible)
∴ y = 2z ⇒ Infinitely many solutions does not exist.
For x = 2z, lets take x = 2, z = 1, y = y
Substitute (2,y,1)in system of equations ⇒ y = -2
∴For each pair of (x,z), we get a value of y.
Therefore, for x = 2z infinitely many solutions exists.
Answer: (b)
12. If p -> (p ∧~ q) is false. Then the truth values of p and q are respectively
a. F, T
b. T, F
c. F, F
d. T, T
Given p ->(p ∧~ q)
Truth table:
|
p
|
q
|
~q
|
(p ∧~ q)
|
p->(p ∧~ q)
|
|
T
|
T
|
F
|
F
|
F
|
|
T
|
F
|
T
|
T
|
T
|
|
F
|
T
|
F
|
F
|
T
|
|
F
|
F
|
T
|
F
|
T
|
p→(p ∧~ q) is false when p is true and q is true.
Answer: (d)
13. The length of minor axis (along y-axis) of an ellipse of the standard form is 4/√3. If this ellipse touches the line x + 6y = 8, then its eccentricity is:
a. (1/2)(√5/3)
b. (1/2)√(11/3)
c. √(5/6)
d. (1/3)√(11/3)
If 2b = 4/√3
b = 2/√3
Comparing y = (-x/6)+(8/6) with y = mx ±√(a2m2+b2)
m = -1/6 and a2m2 + b2 = 16 / 9
(a2/36) + (4/3) = 16/9
(a2/36) = (16/9) – (4/3)
a2 = 16
e = √(1-b2/a2)
e = √(11/12)
Answer: (b)
14. If z be a complex number satisfying |Re(z)|+|Im(z)| = 4, then |𝑧| cannot be:
a. √7
b. √(17/2)
c. √10
d. √8
|Re(z)|+|Im(z)| = 4
Let z = x+iy
⇒|x|+|y| = 4

z lies on the rhombus.
Maximum value of |z| = 4 when z = 4, -4, 4i, -4i
Minimum value of |z| = 2√2 when z = 2±2i, ±2+2i
|z|∈[2√2 ,4]
|z|∈[√8 ,√16]
|z| ≠ √7
Answer: (a)
15. If \(\begin{array}{l}x = \sum_{n=0}^{\infty }(-1)^{n}\tan ^{2n}\theta\end{array} \)
and \(\begin{array}{l}y = \sum_{n=0}^{\infty }\cos ^{2n}\theta\end{array} \)
where 0 < θ < π/4, then:
a. y(1+x) = 1
b. x(1-y) = 1
c. y(1-x) = 1
d. x(1+y) = 1
y = 1+cos2 θ +cos4 θ + …
\(\begin{array}{l}y =\frac{1}{1-\cos ^{2}\theta }\end{array} \)
1/y = sin2 θ
x = 1-tan2 θ + tan4 θ-…
\(\begin{array}{l}x =\frac{1}{1-(-\tan ^{2}\theta) } = \cos ^{2}\theta\end{array} \)
x +(1/y) = 1
y(1-x) = 1
Answer: (c)
16. If \(\begin{array}{l}\frac{dy}{dx}= \frac{xy}{x^{2}+y^{2}}\end{array} \)
, y(1) = 1, then a value of x satisfying y(x)= e is:
a. √3e
b. (1/2)√3e
c. √2e
d. e/√2
Let y = vx
dy/dx = v+x(dv/dx)
v+x(dv/dx) = vx2/(x2(1+v2) = v/(1+v2)
x(dv/dx) = -v3/(1+v2)
(1/x)dx = (-1/v3)-(1/v)dv
log x = (1/2v2)-log v + log c
log x = (x2/2y2 )-log y + log x + log c
log c + (x2/2y2) – log y = 0
y(1) = 1
log C + (1/2)-0 = 0
log c = −1/2
y(x) = e
-(1/2) + (x2/2e2)-1 = 0
x2/e2 = 3
x = ±√3e
Answer: (a)
17. If one end of focal chord AB of the parabola y2 = 8x is at A(1/2,-2) , then the equation of tangent to it at B is
a. x+2y+8 = 0
b. 2x-y-24 = 0
c. x-2y+8 = 0
d. 2x+y-24 = 0
Let PQ be the focal chord of the parabola y2 = 8x
P(t1) = (2t12, 4t1) and Q(t2) = (2t22, 4t2)
t1t2 = -1
(1/2, -2) is one of the ends of the focal chord of the parabola
Let (1/2, -2) = (2t22, 4t2)
Other end of focal chord will have parameter t1= 2
The co-ordinate of the other end of the focal chord will be (8,8).
The equation of the tangent will be given as 8y = 4(x+8)
⇒2y−x = 8
Answer:(c)
18. Let an be the nth term of a G.P. of positive terms. If \(\begin{array}{l}\sum_{n=1}^{100}a_{2n+1}= 200\end{array} \)
and \(\begin{array}{l}\sum_{n=1}^{100}a_{2n}= 100\end{array} \)
a. 300
b. 175
c. 225
d. 150
an is a positive term of GP.
Let GP be a, ar, ar2,…..
\(\begin{array}{l}\sum_{n=1}^{100}a_{2n+1}= 200\end{array} \)
= a3+a5+a7+…+a201
200 = ar2 + ar4 + …+ar201
200 =
\(\begin{array}{l}\frac{ar^{2}(r^{200}-1)}{r^{2}-1}\end{array} \)
…(i)
Also,
\(\begin{array}{l}\sum_{n=1}^{100}a_{2n}= 100\end{array} \)
100 = a2 + a4+ …+a200
100 = ar + ar3 + …ar199
100 =
\(\begin{array}{l}\frac{ar(r^{200}-1)}{r^{2}-1}\end{array} \)
..(ii)
From (i) and (ii), r = 2
And
\(\begin{array}{l}\sum_{n=1}^{100}a_{2n+1} + \sum_{n=1}^{100}a_{2n}= 300\end{array} \)
a2 + a3+a4 ….+a200+a201 = 300
ar + ar2+ar3+…ar200 = 300
r(a+ar+ar2+…+ar199) = 300
2(a1+a2+a3+…+a200) = 300
\(\begin{array}{l}\sum_{n=1}^{200}a_{n} = 150\end{array} \)
Answer: (d)
19. A random variable X has the following probability distribution:
|
X
|
1
|
2
|
3
|
4
|
5
|
|
P(X)
|
K2
|
2K
|
K
|
2K
|
5K2
|
Then P(X>2) is equal to:
a. 7/12
b. 23/36
c. 1/36
d. 1/6
We know that
\(\begin{array}{l}\sum_{X=1}^{5}P(X) = 1\end{array} \)
K2 +2K+K+2K+5K2 = 1
6K2+5K-1 = 0
6K (K+1)-(K+1) = 0
(K+1)(6K-1) = 0
K = -1 or K = 1/6
K cannot be negative.
P(X>2) = P(X = 3) + P(X = 4)+ P(X = 5)
= K+2K + 5K2
= (1/6) + 2(1/6) +5(1/6)2
= 23/36
Answer: (b)
20. If \(\begin{array}{l}\int \frac{d\theta }{\cos ^{2}\theta (\tan 2\theta +\sec 2\theta )}= \lambda \tan \theta +2\: log_{e}\left | f(\theta ) \right |+C\end{array} \)
where C is constant if integration, then the ordered pair (λ, f(θ)) is equal to:
a. (-1, 1-tan θ)
b. (-1, 1+tan θ)
c. (1, 1+tan θ)
d. (1, 1-tan θ)
Let
\(\begin{array}{l}I=\int \frac{d \theta}{\cos ^{2} \theta(\sec 2 \theta+\tan 2 \theta)}\end{array} \)
\(\begin{array}{l}I=\int \frac{\sec ^{2} \theta d \theta}{\left(\frac{1+\tan ^{2} \theta}{1-\tan ^{2} \theta}\right)+\left(\frac{2 \tan \theta}{1-\tan ^{2} \theta}\right)}\end{array} \)
\(\begin{array}{l}I=\int \frac{\left(1-\tan ^{2} \theta\right)\left(\sec ^{2} \theta\right) d \theta}{(1+\tan \theta)^{2}}\end{array} \)
Let tan θ= k
sec2 θ = dk
\(\begin{array}{l}I=\int \frac{\left(1-k^{2}\right)}{(1+k)^{2}} d k=\int \frac{(1-k)}{(1+k)} d k\end{array} \)
I = (2/(1+k))-1)dk
I = 2 lnǀ1+kǀ -k+c
I = 2 lnǀ1+tan θǀ -tan θ +c
Given I = tan θ+ 2 log f(θ) + c
λ= -1, f(θ) = ǀ1+ tan θǀ
Answer: (b)
21. Let \(\begin{array}{l}\vec{a}\end{array} \)
, \(\begin{array}{l}\vec{b}\end{array} \)
, and \(\begin{array}{l}\vec{c}\end{array} \)
be three vectors such that \(\begin{array}{l}\vec{a}=\sqrt{3}\end{array} \)
, \(\begin{array}{l}\vec{b}=5\end{array} \)
, \(\begin{array}{l}\vec{b}.\vec{c}=10\end{array} \)
and the angle between \(\begin{array}{l}\vec{b}\end{array} \)
and \(\begin{array}{l}\vec{c}\end{array} \)
is π/3. If \(\begin{array}{l}\vec{a}\end{array} \)
is perpendicular to \(\begin{array}{l}\vec{b}\times \vec{c}\end{array} \)
, then \(\begin{array}{l}\left | \vec{a}\times (\vec{b}\times \vec{c} )\right |\end{array} \)
is equal to
\(\begin{array}{l}\left | \vec{a}\times (\vec{b}\times \vec{c} )\right | = \left | \vec{a} \right |\left | \vec{b} \times \vec{c}\right |\sin \theta\end{array} \)
where θ is the angle between \(\begin{array}{l}\vec{a}\end{array} \)
and \(\begin{array}{l}\vec{b}\times \vec{c}\end{array} \)
.

\(\begin{array}{l}\left | \vec{c} \right | = 4\end{array} \)
\(\begin{array}{l}\left |\vec{a}\times(\vec{b}\times \vec{c}) \right | = 30\end{array} \)
Answer : (30)
22. If Cr = 25Cr and C0+5⋅C1+9⋅C2 +⋯+101. C25 =225 .k then k is equal to
S = 25C0 + 525C1 + 925C2 + ….+9725C24 +10125C25 = 225k ..(i)
Reverse and apply property nCr = nCn-r in all coefficients
S = 10125C0 + 9725C1+…+525C24+25C25 …(ii)
Adding (i) and (ii)
2S = 102[25C0+25C1+…+25C5]
S = 51×225
k = 51
Answer: (51)
23. If the curves x2 -6x +y2 +8 = 0 and x2-8y+y2+16-k = 0, (k>0) touch each other at a point, then the largest value of k is
Two circles touch each other if C1C2 = ǀr1± r2ǀ
√k +1 = 5 or ǀ√k-1ǀ = 5
k = 16 or 36
Maximum value of k is 36.
Answer: (36)
24. The number of terms common to the A.P.’s 3,7,11,…407 and 2,9,16,…709 is .
First common term is 23
Common difference = LCM(7,4) = 28
23+(n−1)28 ≤ 407
n−1 ≤ 13.71
n = 14
Answer: (14)
25. If the distance between the plane, 23x-10y-2z+48 = 0 and the plane containing the lines \(\begin{array}{l}\frac{x+1}{2}=\frac{y-3}{4}=\frac{z+1}{3}\end{array} \)
and \(\begin{array}{l}\frac{x+3}{2}=\frac{y+2}{6}=\frac{z-1}{\lambda }\end{array} \)
, λ∈ R is equal to \(\begin{array}{l}\frac{k}{\sqrt{633}}\end{array} \)
, then k is equal to:
We find the point of intersection of the two lines, and the distance of given plane from the two lines is the distance of plane from the point of intersection.
(2p-1, 4p+3, 3p-1) = (2q-3, 6q-2, λq+1)
p = -1/2 and q = 1/2
λ= -7
Point of intersection is (-2,1,-5/2)
\(\begin{array}{l}\frac{k}{\sqrt{633}}=\left|\frac{-46-10+5+48}{\sqrt{633}}\right|\end{array} \)
k = 3
Answer: (3)
Video Lessons – January 9 Shift 2 Maths
Download PDF 
carouselExampleControls112
























Comments