The JEE Main 2022 July 26 – Shift 2 Maths Question Paper with Solutions is given on this page. Practising the JEE Main 2022 question papers is an effective way to prepare for any engineering entrance examination. So students are advised to revise and practise the JEE Main 2022 question paper with solutions. JEE Main 2022 answer keys consist of accurate answers solved by a team of experts at BYJU’S.
JEE Main 2022 July 26th Shift 2 Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. The minimum value of the sum of the squares of the roots of x2 + (3 – a)x + 1 = 2a is
(A) 4
(B) 5
(C) 6
(D) 8
Answer (C)
Sol.
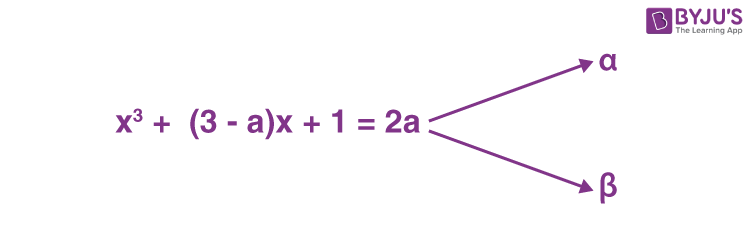
α + β = a – 3, αβ = 1 – 2a
⇒ α2 + β2 = (a – 3)2 – 2(1– 2a)
= a2 – 6a + 9 – 2 + 4a
= a2 – 2a + 7
= (a – 1)2 + 6
So,
\(\begin{array}{l} \alpha^2+\beta^2\geq6 \end{array} \)
2. If z = x + iy satisfies | z | – 2 = 0 and |z – i| – | z + 5i| = 0, then
(A) x + 2y – 4 = 0
(B) x2 + y – 4 = 0
(C) x + 2y + 4 = 0
(D) x2 – y + 3 = 0
Answer (C)
Sol.
\(\begin{array}{l} \left|z-i\right|=\left|z+5i\right|\end{array} \)
So, z lies on ⊥r bisector of (0, 1) and (0, –5)
i.e., liney = –2
as |z| = 2
⇒ z = –2i
x = 0 and y = –2
so, x + 2y + 4 = 0
3. Let \(\begin{array}{l} A=\begin{bmatrix}1 \\ 1\\1\end{bmatrix}\text{ and }B=\begin{bmatrix}9^2 & -10^2 & 11^2 \\12^2 & 13^2 & -14^2 \\-15^2 & 16^2 & 17^2 \\\end{bmatrix},\end{array} \)
then the value of A′BA is
(A) 1224
(B) 1042
(C) 540
(D) 539
Answer (D)
Sol.
\(\begin{array}{l} A’BA=\begin{bmatrix}1 & 1 & 1 \\\end{bmatrix}\begin{bmatrix}9^2 & -10^2 & 11^2 \\12^2 & 13^2 & -14^2 \\-15^2 & 16^2 & 17^2 \\\end{bmatrix}A\end{array} \)
\(\begin{array}{l} =\begin{bmatrix}9^2+12^2-15^2 & -10^2+13^2+16^2 & 11^2-14^2+17^2 \\\end{bmatrix} \begin{bmatrix}1 \\1 \\1\end{bmatrix}\end{array} \)
\(\begin{array}{l} =\left[9^2+12^2-15^2-10^2+13^2+16^2+11^2-14^2+17^2\right]\end{array} \)
= [(92 – 102) + (112 + 122) + (132 – 142) + (162 – 152) + 172]
= [–19 + 265 + (–27) + 31 + 289]
= [585 – 46] = [539]
4. \(\begin{array}{l} \sum_{\underset{i\neq j}{i, j=0}}^{n}{^n}C_i\ ^nC_j\end{array} \)
is equal to
\(\begin{array}{l}\left(A\right) 2^{2n} – ^{2n}C_n \end{array} \)
\(\begin{array}{l}\left(B\right) 2^{2n-1} – ^{2n-1}C_{n-1} \end{array} \)
\(\begin{array}{l} (\text{C})\ 2^{2n}-\frac{1}{2}\ ^{2n}C_n\end{array} \)
\(\begin{array}{l} (\text{D})\ 2^{n-1}+2^{2n-1}C_n\end{array} \)
Answer (A*)
Sol.
\(\begin{array}{l} \sum_{\underset{i\neq j}{i, j=0}}^{n} {^n}C_i\ ^nC_j=\sum_{i, j=0}^{n}{^n}C_i\ ^nC_j-\sum_{i=j}^{n}{^n}C_i\ ^nC_j\end{array} \)
\(\begin{array}{l} =\sum_{j=0}^{n}{^n}C_i\sum_{j=0}^{n}{^n}C_j-\sum_{i=0}^{n}{^n}C_i\ C_i\end{array} \)
\(\begin{array}{l} =2^n\cdot2^n-\ ^{2n}C_n\end{array} \)
\(\begin{array}{l} =2^{2n}-^{2n}C_n\end{array} \)
5. Let P and Q be any points on the curves (x – 1)2 + (y + 1)2 = 1 and y = x2, respectively. The distance between P and Q is minimum for some value of the abscissa of P in the interval
\(\begin{array}{l} (\text{A})\ \left(0,\frac{1}{4}\right) \end{array} \)
\(\begin{array}{l} (\text{B})\ \left(\frac{1}{2},\frac{3}{4}\right) \end{array} \)
\(\begin{array}{l} (\text{C})\ \left(\frac{1}{4},\frac{1}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \left(\frac{3}{4},1\right)\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} y = mx+2a+\frac{1}{m^2}\text{(Equation of normal to}~ x^2 = 4ay ~\text{in slope form) through} (1, -1).\end{array} \)
\(\begin{array}{l}4m^3 + 6m^2 + 1 = 0\end{array} \)
\(\begin{array}{l} \Rightarrow m\simeq -16 \end{array} \)
\(\begin{array}{l} \text{Slope of normal} \simeq \frac{-8}{5}=\tan\theta\end{array} \)
\(\begin{array}{l} \Rightarrow\ \cos\theta\simeq\frac{-5}{\sqrt{89}},\sin\theta\simeq\frac{8}{\sqrt{89}} \end{array} \)
\(\begin{array}{l} x_p=1+\cos\theta\simeq 1-\frac{5}{\sqrt{89}}\in\left(\frac{1}{4},\frac{1}{2}\right)\end{array} \)
6. If the maximum value of a, for which the function \(\begin{array}{l} f_a\left(x\right)=\tan^{-1}2x-3ax+7\end{array} \)
\(\begin{array}{l}\text{is non-decreasing in}\ \left(-\frac{\pi}{6},\frac{\pi}{6}\right),\ \text{is}\ \overline{a},\ \text{then}\ f_{\overline{a}}\left(\frac{\pi}{8}\right)\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ 8-\frac{9\pi}{4\left(9+\pi^2\right)} \end{array} \)
\(\begin{array}{l} (\text{B})\ 8-\frac{4\pi}{9\left(4+\pi^2\right)} \end{array} \)
\(\begin{array}{l} (\text{C})\ 8\left(\frac{1+\pi^2}{9+\pi^2}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ 8-\frac{\pi}{4}\end{array} \)
Answer (*)
Sol.
\(\begin{array}{l} f_a\left(x\right)=\tan^{-1}2x-3ax+7 \end{array} \)
\(\begin{array}{l}\because f_a(x) ~\text{is non}\mbox{-}\text{decreasing in} \left(-\frac{\pi}{6},\frac{\pi}{6}\right)\end{array} \)
\(\begin{array}{l} \therefore\ f_a’\left(x\right)\geq 0 \Rightarrow \frac{2}{1+4x^2}-3a\geq0\end{array} \)
\(\begin{array}{l} \Rightarrow\ 3a\leq\frac{2}{1+4x^2} \end{array} \)
\(\begin{array}{l}\text{So,}~ a_\text{max}=\frac{2}{3}\left(\frac{1}{1+4\times\frac{\pi^2}{36}}\right)=\frac{6}{9+\pi^2}=\overline{a} \end{array} \)
\(\begin{array}{l} \therefore\ f_{\overline{a}}\left(\frac{\pi}{8}\right)=\tan^{-1}\frac{\pi}{4}-3\frac{\pi}{8}\cdot\frac{6}{9+\pi^2}+7\end{array} \)
7. Let \(\begin{array}{l} \beta=\displaystyle \lim_{x \to 0}\frac{\alpha x-\left(e^{3x}-1\right)}{\alpha x\left(e^{3x}-1\right)}\ \text{for some}\ \alpha\ \in\ \mathbb{R}.\end{array} \)
Then the value of α + β is
\(\begin{array}{l} (\text{A})\ \frac{14}{5} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3}{2} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{5}{2} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{7}{2} \end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} \beta=\displaystyle \lim_{x \to 0}\frac{\alpha x-\left(e^{3x}-1\right)}{\alpha x\left(e^{3x}-1\right)}, \alpha\ \in\ \mathbb{R}\end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{x \to 0} \frac{\frac{\alpha}{3}-\left(\frac{e^{3x}-1}{3x}\right)}{\alpha x\left(\frac{e^{3x-1}}{3x}\right)}\end{array} \)
So, α = 3 (to make indeterminant form)
\(\begin{array}{l} \beta=\displaystyle \lim_{x \to 0}\frac{1-\left(\frac{e^{3x}-1}{3x}\right)}{3x}=\frac{1-\frac{\left(3x+\frac{9x^2}{2}+\cdots\right)}{3x}}{3x}\end{array} \)
\(\begin{array}{l} =\frac{-\left(\frac{9}{2}x^2+\frac{\left(3x\right)^3}{31}+\cdots\right)}{9x^2} =\frac{-1}{2}\end{array} \)
\(\begin{array}{l} \therefore\ \alpha +\beta=3-\frac{1}{2}=\frac{5}{2}\end{array} \)
8. The value of \(\begin{array}{l} \text{log}_e2\frac{d}{dx}\left(\text{log}_{\cos x}\text{cosec x}\right) \textup{ at }x=\frac{\pi}{4}\end{array} \)
is
\(\begin{array}{l} (\text{A})\ -2\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{B})\ 2\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{C})\ -4\end{array} \)
\(\begin{array}{l} (\text{D})\ 4\end{array} \)
Answer (D)
Sol. Let
\(\begin{array}{l} f\left(x\right)=\text{log}_{\cos x} \text{cosec}x\end{array} \)
\(\begin{array}{l} =\frac{\text{log }\text{cosec}x}{\text{log cos}x}\end{array} \)
\(\begin{array}{l} f’\left(x\right)=\frac{\text{log cos}x\cdot\sin x\cdot \left(-\text{cosec}x\cot x-\text{log cosec}x\cdot\frac{1}{\cos x}\cdot-\sin x\right)}{\left(\text{log cos}x\right)^2}\end{array} \)
at x = π/4
\(\begin{array}{l}f’\left(\frac{\pi}{4}\right)= \frac{-log (\frac{1}{\sqrt2})+log\sqrt2}{(log \frac{1}{\sqrt2})^2}\end{array} \)
\(\begin{array}{l}=\frac{2}{log \sqrt2}\end{array} \)
\(\begin{array}{l} \therefore\ \text{log}_e\ 2f’\left(x\right)\text{ at }x=\frac{\pi}{4}=4\end{array} \)
9. \(\begin{array}{l} \displaystyle\int\limits_0^{20\pi}\left(\left|\sin x\right|+\left|\cos x\right|\right)^2 dx\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ 10\left(\pi+4\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ 10\left(\pi+2\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ 20\left(\pi-2\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ 20\left(\pi+2\right)\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} I=\displaystyle\int\limits_0^{20\pi}\left(\left|\sin x\right|+\left|\cos x\right|\right)^2 dx\end{array} \)
\(\begin{array}{l} =20\displaystyle\int\limits_0^\pi\left(1+\left|\sin 2x\right|\right)dx\end{array} \)
\(\begin{array}{l} =40\displaystyle\int\limits_0^\frac{\pi}{2}\left(1+\sin 2x\right)dx\end{array} \)
\(\begin{array}{l} \left. =40\left(x-\frac{\cos 2x}{2}\right)\right|_0^{\frac{\pi}{2}}\end{array} \)
\(\begin{array}{l} =40\left(\frac{\pi}{2}+\frac{1}{2}+\frac{1}{2}\right)=20\left(\pi+2\right)\end{array} \)
10. Let the solution curve y = f(x) of the differential equation \(\begin{array}{l} \frac{dy}{dx}+\frac{xy}{x^2-1}=\frac{x^4+2x}{\sqrt{1-x^2}},x \in \left(-1, 1\right)\end{array} \)
pass through the origin. Then \(\begin{array}{l} \displaystyle\int\limits_{-\frac{\sqrt{3}}{2}}^{\frac{\sqrt{3}}{2}}f\left(x\right)dx\end{array} \)
is
\(\begin{array}{l} (\text{A})\ \frac{\pi}{3}-\frac{1}{4}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{\pi}{3}-\frac{\sqrt{3}}{4}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{\pi}{6}-\frac{\sqrt{3}}{4}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{\pi}{6}-\frac{\sqrt{3}}{2}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \frac{dy}{dx}+\frac{xy}{x^2-1}=\frac{x^4+2x}{\sqrt{1-x^2}}\end{array} \)
which is first order linear differential equation.
\(\begin{array}{l}\text{Integrating factor (I.F.) = } e^{\int\frac{x}{x^2-1}dx} \end{array} \)
\(\begin{array}{l} =e^{\frac{1}{2}\text{ln}\left|x^2-1\right|}=\sqrt{\left|x^2-1\right|}\end{array} \)
\(\begin{array}{l} =\sqrt{1-x^2}\ \because x\in \left(-1, 1\right)\end{array} \)
Solution of differential equation
\(\begin{array}{l} y\sqrt{1-x^2}=\int\left(x^4+2x\right)dx=\frac{x^5}{5}+x^2+c\end{array} \)
Curve is passing through origin, c = 0
\(\begin{array}{l} y=\frac{x^5+5x^2}{5\sqrt{1-x^2}} \end{array} \)
\(\begin{array}{l} \displaystyle\int\limits_\frac{-\sqrt{3}}{2}^{\frac{\sqrt{3}}{2}}\frac{x^5+5x^2}{5\sqrt{1-x^2}}dx=0+2\displaystyle\int\limits_0^{\frac{\sqrt{3}}{2}}\frac{x^2}{\sqrt{1-x^2}}dx\end{array} \)
\(\begin{array}{l} \text{put}\ x = sin\theta \\dx = cos\theta~ d\theta\end{array} \)
\(\begin{array}{l} I=2\displaystyle\int\limits_0^\frac{\pi}{3}\frac{\sin^2\theta\cdot\cos\theta d\theta}{\cos\theta}\end{array} \)
\(\begin{array}{l} =\displaystyle\int\limits_0^\frac{\pi}{3}\left(1-\cos 2\theta \right)d\theta\end{array} \)
\(\begin{array}{l} \left.=\left(\theta-\frac{\sin 2\theta}{2}\right)\right| _0^\frac{\pi}{3}\end{array} \)
\(\begin{array}{l} =\frac{\pi}{3}-\frac{\sqrt{3}}{4} \end{array} \)
11. The acute angle between the pair of tangents drawn to the ellipse 2x2 + 3y2 = 5 from the point (1, 3) is
\(\begin{array}{l} (\text{A})\ \tan^{-1}\left(\frac{16}{7\sqrt{5}}\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ \tan^{-1}\left(\frac{24}{7\sqrt{5}}\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \tan^{-1}\left(\frac{32}{7\sqrt{5}}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \tan^{-1}\left(\frac{3+8\sqrt{5}}{35}\right)\end{array} \)
Answer (B)
Sol. 2x2 + 3y2 = 5
Equation of tangent having slope m.
\(\begin{array}{l} y=mx\pm\sqrt{\frac{5}{2}m^2+\frac{5}{3}}\end{array} \)
which passes through (1, 3)
\(\begin{array}{l} 3=m\pm\sqrt{\frac{5}{2}m^2+\frac{5}{3}}\end{array} \)
\(\begin{array}{l} \frac{5}{2}m^2+\frac{5}{3}=9+m^2-6m \end{array} \)
\(\begin{array}{l} \frac{3}{2}m^2+6m-\frac{22}{3}=0\end{array} \)
\(\begin{array}{l} 9m^2+36m-44=0\end{array} \)
\(\begin{array}{l} m_1+m_2=-4, m_1m_2=-\frac{44}{9} \end{array} \)
\(\begin{array}{l} \left(m_1-m_2\right)^2=16+4\times\frac{44}{9}=\frac{320}{9} \end{array} \)
Acute angle between the tangents is given by
\(\begin{array}{l} \alpha = \tan^{-1}\left|\frac{m_1-m_2}{1+m_1m_2}\right| \end{array} \)
\(\begin{array}{l} =\tan^{-1}\left|\frac{\frac{8\sqrt{5}}{3}}{1-\frac{44}{9}}\right| \end{array} \)
\(\begin{array}{l} =\tan^{-1}\left(\frac{24\sqrt{5}}{35}\right)\end{array} \)
\(\begin{array}{l} \alpha =\tan^{-1}\left(\frac{24}{7\sqrt{5}}\right)\end{array} \)
12. The equation of a common tangent to the parabolas y = x2 and y = –(x – 2)2 is
(A) y = 4(x – 2)
(B) y = 4(x – 1)
(C) y = 4(x + 1)
(D) y = 4(x + 2)
Answer (B)
Sol. Equation of tangent of slope m to y = x2
\(\begin{array}{l} y=mx-\frac{1}{4}m^2 \end{array} \)
Equation of tangent of slope m to y = –(x – 2)2
\(\begin{array}{l} y=m\left(x-2\right)+\frac{1}{4}m^2\end{array} \)
If both equation represent the same line
\(\begin{array}{l} \frac{1}{4}m^2-2m=-\frac{1}{4}m^2\end{array} \)
m = 0, 4
So, equation of tangent
\(\begin{array}{l} y=4x-4\end{array} \)
13. Let the abscissae of the two points P and Q on a circle be the roots of x2 – 4x – 6 = 0 and the ordinates of P and Q be the roots of y2 + 2y – 7 = 0. If PQ is a diameter of the circle x2 + y2 + 2ax + 2by + c = 0, then the value of (a + b – c) is
(A) 12
(B) 13
(C) 14
(D) 16
Answer (A)
Sol. Abscissae of PQ are roots of x2 – 4x – 6 = 0
Ordinates of PQ are roots of y2 + 2y – 7 = 0
and PQ is diameter
\(\begin{array}{l} \Rightarrow \text{Equation of circle is}~x^2+y^2-4x+2y-13=0\end{array} \)
But, given
\(\begin{array}{l} x^2+y^2+2ax+2by+c=0\end{array} \)
By comparison a = –2, b = 1, c = –13
⇒ a + b – c = –2 + 1 + 13 = 12
14. If the line x – 1 = 0 is a directrix of the hyperbola kx2 – y2 = 6, then the hyperbola passes through the point
\(\begin{array}{l} (\text{A})\ \left(-2\sqrt{5},6\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ \left(-\sqrt{5},3\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \left(\sqrt{5},-2\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \left(2\sqrt{5},3\sqrt{6}\right)\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\text{Given hyperbola :} \frac{x^2}{6/k}-\frac{y^2}{6}=1 \end{array} \)
\(\begin{array}{l}\text{Eccentricity }= e = \sqrt{1+\frac{6}{6/k}}=\sqrt{1+k}\end{array} \)
\(\begin{array}{l}\text{Directrices }: x=\pm\frac{a}{e}\Rightarrow x=\pm \frac{\sqrt{6}}{\sqrt{k}\sqrt{k+1}}\end{array} \)
\(\begin{array}{l}\text{As given} : \frac{\sqrt{6}}{\sqrt{k}\sqrt{k+1}}=1\end{array} \)
\(\begin{array}{l} \Rightarrow k = 2 \end{array} \)
\(\begin{array}{l}\text{Here hyperbola is } \frac{x^2}{3}-\frac{y^2}{6}=1 \end{array} \)
Checking the option gives
\(\begin{array}{l} \left(\sqrt{5},-2\right)\text{satisfies it.}\end{array} \)
15. A vector \(\begin{array}{l}\vec{a}\end{array} \)
is parallel to the line of intersection of the plane determined by the vectors \(\begin{array}{l} \hat{i},\hat{i}+\hat{j}\end{array} \)
and the plane determined by the vectors \(\begin{array}{l} \hat{i}-\hat{j},\hat{i}+\hat{k}. \end{array} \)
The obtuse angle between\(\begin{array}{l}\vec{a}\ \text{and the vector}\ \vec{b}=\hat{i}-2\hat{j}+2\hat{k}\end{array} \)
is
\(\begin{array}{l} (\text{A})\ \frac{3\pi}{4} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{2\pi}{3} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{4\pi}{5} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{5\pi}{6}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}\text{If}\ \vec{n}_1\ \text{is a vector normal to the plane determined by}\ \hat{i}\text{ and }\hat{i}+\hat{j}\end{array} \)
then
\(\begin{array}{l} \vec{n}_1=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\1 & 0 & 0 \\1 & 1 & 0 \\\end{vmatrix}=\hat{k}\end{array} \)
\(\begin{array}{l}\text{If}\ \vec{n}_2\ \text{is a vector normal to the plane determined by}\ \hat{i}-\hat{j}\ \text{and}\ \hat{i}+\hat{k}\end{array} \)
then
\(\begin{array}{l} \vec{n}_2=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\1 & -1 & 0 \\1 & 0 & 1 \\\end{vmatrix}=-\hat{i}-\hat{j}+\hat{k}\end{array} \)
\(\begin{array}{l}\text{Vector}\ \vec{a}\ \text{is parallel to}\ \vec{n}_1\times \vec{n}_2\end{array} \)
i.e.
\(\begin{array}{l}\vec{a}\ \text{is parallel to}\ \begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\0 & 0 & 1 \\-1 & -1 & 1 \\\end{vmatrix} =\hat{i}-\hat{j}\end{array} \)
Given
\(\begin{array}{l} \vec{b}=\hat{i}-2\hat{j}+2\hat{k}\end{array} \)
Cosine of acute angle between
\(\begin{array}{l} \vec{a}\text{ and }\vec{b}=\left|\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\cdot\left|\vec{b}\right|}\right|=\frac{1}{\sqrt{2}}\end{array} \)
Obtuse angle between
\(\begin{array}{l} \vec{a}\text{ and }\vec{b}=\frac{3\pi}{4}\end{array} \)
16. If \(\begin{array}{l} 0<x<\frac{1}{\sqrt{2}}\ \text{and}\ \frac{\sin^{-1}x}{\alpha}=\frac{\cos^{-1}x}{\beta}\end{array} \)
then a value of \(\begin{array}{l} \sin\left(\frac{2\pi\alpha}{\alpha+\beta}\right)\end{array} \)
is
\(\begin{array}{l} (\text{A})\ 4\sqrt{\left(1-x^2\right)}\left(1-2x^2\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ 4x\sqrt{\left(1-x^2\right)}\left(1-2x^2\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ 2x\sqrt{\left(1-x^2\right)}\left(1-4x^2\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ 4\sqrt{\left(1-x^2\right)}\left(1-4x^2\right)\end{array} \)
Answer (B)
Sol. Let
\(\begin{array}{l} \frac{\sin^{-1}x}{\alpha}=\frac{\cos^{-1}x}{\beta}=k\Rightarrow \sin^{-1}x+\cos^{-1}x=k\left(\alpha+\beta\right)\end{array} \)
\(\begin{array}{l} \Rightarrow \alpha+\beta=\frac{\pi}{2k}.\end{array} \)
Now,
\(\begin{array}{l} \frac{2\pi\alpha}{\alpha+\beta}=\frac{2\pi\alpha}{\frac{\pi}{2k}}=4k\alpha=4\sin^{-1}x \end{array} \)
Here
\(\begin{array}{l} \sin\left(\frac{2\pi\alpha}{\alpha+\beta}\right)=\sin\left(4\sin^{-1}x\right)\end{array} \)
Let
\(\begin{array}{l} \sin^{-1}x = \theta \because x \in \left(0,\frac{1}{\sqrt{2}}\right)\Rightarrow \theta \in \left(0, \frac{\pi}{4}\right)\end{array} \)
\(\begin{array}{l} \Rightarrow x = sin \theta\end{array} \)
\(\begin{array}{l} \Rightarrow \cos\theta=\sqrt{1-x^2} \end{array} \)
\(\begin{array}{l} \Rightarrow \sin2\theta=2x\cdot\sqrt{1-x^2} \end{array} \)
\(\begin{array}{l} \Rightarrow \cos2\theta=\sqrt{1-4x^2\left(1-x^2\right)}=\sqrt{\left(2x^2-1\right)^2}=1-2x^2\end{array} \)
\(\begin{array}{l} \left(\because \cos2\theta > 0 \text{ as } 2\theta \in \left(0,\frac{\pi}{2}\right)\right) \end{array} \)
\(\begin{array}{l} \Rightarrow \sin4\theta=2\cdot 2x\sqrt{1-x^2}\left(1-2x^2\right)\end{array} \)
\(\begin{array}{l} =4x\sqrt{1-x^2}\left(1-2x^2\right) \end{array} \)
17. Negation of the Boolean expression p⇔ (q⇒p) is
(A) (~ p) ∧q (B) p∧ (~ q)
(C) (~ p) ∨ (~ q) (D) (~ p) ∧ (~ q)
Answer (D)
Sol. p⇔ (q⇒p)
~ (p⇔ (q⇔p))
≡p⇔ ~ (q⇒p)
≡p⇔ (q∧ ~ p)
≡ (p⇒ (q∧ ~ p)) ∧ ((q∧ ~ p) ⇒p))
≡ (~ p∨ (q∧ ~ p)) ∧ ((~ q∨p) ∨p))
≡ ((~ p∨q) ∧ ~ p) ∧ (~ q∨p)
≡ ~ p∧ (~ q∨p)
≡ (~ p∧ ~ q) ∨ (~ p∧p)
≡ (~ p∧ ~ q) ∨c
≡ (~ p∧ ~ q)
18. Let X be a binomially distributed random variable with mean 4 and variance 4/3. Then, 54 P(X≤ 2) is equal to
\(\begin{array}{l} (\text{A})\ \frac{73}{27}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{146}{27}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{146}{81}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{126}{81}\end{array} \)
Answer (B)
Sol. Mean = 4 = μ = np
\(\begin{array}{l}Variance = \sigma^2=np\left(1-P\right)=\frac{4}{3}\end{array} \)
\(\begin{array}{l} 4\left(1-P\right)=\frac{4}{3}\end{array} \)
\(\begin{array}{l} P=\frac{2}{3} \end{array} \)
\(\begin{array}{l} n\times\frac{2}{3}=4 \\n = 6\end{array} \)
\(\begin{array}{l} P\left(X=k\right)=\ ^nC_k\ P^k\left(1-P\right)^{n-k} \end{array} \)
\(\begin{array}{l} P\left(X\leq 2\right)=P\left(X=0\right)+P\left(X=1\right)+P\left(X=2\right)\end{array} \)
\(\begin{array}{l} =\ ^6C_0P^0\left(1-p\right)^6+\ ^6C_1P^1\left(1-P\right)^5+\ ^6C_2P^2\left(1-P\right)^4\end{array} \)
\(\begin{array}{l} =\ ^6C_0\left(\frac{1}{3}\right)^6+\ ^6C_1\left(\frac{2}{3}\right)\left(\frac{1}{3}\right)^5+\ ^6C_2\left(\frac{2}{3}\right)^2\left(\frac{1}{3}\right)^4\end{array} \)
\(\begin{array}{l} =\left(\frac{1}{3}\right)^6\left[1+12+60\right]=\frac{73}{3^6}\end{array} \)
\(\begin{array}{l}54P(X\le 2)=\frac{73}{3^6}\times 54 =\frac{146}{27} \end{array} \)
19. The integral \(\begin{array}{l} \int\frac{\left(1-\frac{1}{\sqrt{3}}\right)\left(\cos x-\sin x\right)}{\left(1+\frac{2}{\sqrt{3}}\sin 2x\right)}dx\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ \frac{1}{2}\text{log}_e\left|\frac{\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)}{\tan\left(\frac{x}{2}+\frac{\pi}{6}\right)}\right|+C\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{1}{2}\text{log}_e\left|\frac{\tan\left(\frac{x}{2}+\frac{x}{6}\right)}{\tan\left(\frac{x}{2}+\frac{\pi}{3}\right)}\right|+C\end{array} \)
\(\begin{array}{l} (\text{C})\ \text{log}_e\left|\frac{\tan\left(\frac{x}{2}+\frac{\pi}{6}\right)}{\tan\left(\frac{x}{2}+\frac{\pi}{12}\right)}\right|+C\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{1}{2}\text{log}_e\left|\frac{\tan\left(\frac{x}{2}-\frac{\pi}{12}\right)}{\tan\left(\frac{x}{2}-\frac{\pi}{6}\right)}\right|+C\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} =\int\frac{\left(1-\frac{1}{\sqrt{3}}\right)\left(\cos x-\sin x\right)}{\left(1+\frac{2}{\sqrt{3}}\sin 2x\right)}dx\end{array} \)
\(\begin{array}{l} =\int\frac{\left(\frac{\sqrt{3}-1}{\sqrt{3}}\right)\sqrt{2}\sin\left(\frac{\pi}{4}-x\right)}{\left(\frac{2}{\sqrt{3}}\right)\left(\sin\frac{\pi}{3}+\sin 2x\right)}dx\end{array} \)
\(\begin{array}{l} =\int\frac{\frac{\left(\sqrt{3}-1\right)}{\sqrt{2}}\sin \left(\frac{\pi}{4}-x\right)}{\left(\sin\frac{\pi}{3}+\sin2x\right)}dx\end{array} \)
\(\begin{array}{l} =\int\frac{\frac{\sqrt{3}-1}{2\sqrt{2}}\sin\left(\frac{\pi}{4}-x\right)}{\sin\left(\frac{\pi}{6}+x\right)\cos\left(\frac{\pi}{6}-x\right)}dx\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\int\frac{2\sin \frac{\pi}{12}\sin\left(\frac{\pi}{4}-x\right)}{\sin\left(\frac{\pi}{6}+x\right)\cos \left(\frac{\pi}{6}-x\right)}dx\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\int\frac{\cos\left(\frac{\pi}{6}-x\right)-\cos\left(\frac{\pi}{3}-x\right)}{\sin\left(\frac{\pi}{6}+x\right)\cos\left(\frac{\pi}{6}-x\right)}dx\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left[\int\text{cosec}\left(\frac{\pi}{6}+x\right)dx-\int\sec\left(\frac{\pi}{6}-x\right)dx\right]\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left[\text{In}\left|\tan\left(\frac{\pi}{12}+\frac{x}{2}\right)\right|-\int\text{cosec}\left(\frac{\pi}{3}-x\right)dx\right]\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left[\text{In}\left|\tan\left(\frac{\pi}{12}+\frac{x}{2}\right)\right|-\text{In}\left|\frac{\pi}{6}+\frac{x}{2}\right|\right]+C\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\text{In}\left|\frac{\tan\left(\frac{\pi}{12}+\frac{x}{2}\right)}{\tan\left(\frac{\pi}{6}+\frac{x}{2}\right)}\right|+C\end{array} \)
20. The area bounded by the curves y = |x2 – 1| and y = 1 is
\(\begin{array}{l} (\text{A})\ \frac{2}{3}\left(\sqrt{2}+1\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{4}{3}\left(\sqrt{2}-1\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ 2\left(\sqrt{2}-1\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{8}{3}\left(\sqrt{2}-1\right)\end{array} \)
Answer (D)
Sol.
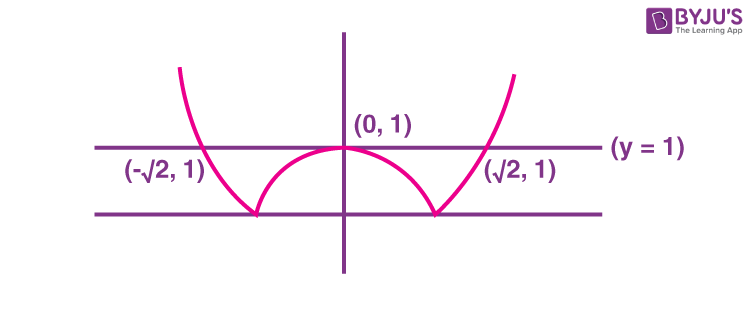
\(\begin{array}{l} \text{ Area } =2\displaystyle\int\limits_0^{\sqrt{2}}\left(1-\left|x^2-1\right|\right)dx\end{array} \)
\(\begin{array}{l} =2\left[\displaystyle\int\limits_0^1\left(1-\left(1-x^2\right)\right)dx+\displaystyle\int\limits_1^{\sqrt{2}}\left(2-x^2\right)dx\right]\end{array} \)
\(\begin{array}{l} =2\left.\left[\left[\frac{x^3}{3}\right]_0^1+\left[2x-\frac{x^3}{3}\right]_1^{\sqrt{2}}\right]\right]\end{array} \)
\(\begin{array}{l} =2\left(\frac{4\sqrt{2}-4}{3}\right)=\frac{8}{3}\left(\sqrt{2}-1\right) \end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let A = {1, 2, 3, 4, 5, 6, 7} and B = {3, 6, 7, 9}. Then the number of elements in the set {C ⊆ A :Cߏ∩B ≠ φ} is _____________.
Answer (112)
Sol. As Cߏ∩B≠φ, c must be not be formed by {1, 2, 4, 5}
∴ Number of subsets of A = 27 = 128
and number of subsets formed by {1, 2, 4, 5} = 16
∴ Required no. of subsets = 27 – 24 = 128 – 16
= 112
2. The largest value of a, for which the perpendicular distance of the plane containing the lines
\(\begin{array}{l} \vec{r}=\left(\hat{i}+\hat{j}\right)+\lambda\left(\hat{i}+a\hat{j}-\hat{k}\right)\text{ and }\vec{r}=\left(\hat{i}+\hat{j}\right)+\mu \left(-\hat{i}+\hat{j}-a\hat{k}\right)\end{array} \)
from the point (2, 1, 4) is √3, is _____________.
Answer (2*)
Sol. Normal to plane
\(\begin{array}{l} =\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\1 & a & -1 \\-1 & 1 & -a \\\end{vmatrix} \end{array} \)
\(\begin{array}{l} =\hat{i}\left(1-a^2\right)-\hat{j}\left(-a-1\right)+\hat{k}\left(1+a\right)\end{array} \)
\(\begin{array}{l} =\left(1-a\right)\hat{i}+\hat{j}+\hat{k}\end{array} \)
∴ Plane (1 – a) (x – 1) + (y – 1) + z = 0
\(\begin{array}{l}\text{Distance from} (2, 1, 4) ~\text{is} \sqrt{3}\end{array} \)
i.e.
\(\begin{array}{l} \Rightarrow \left|\frac{\left(1-a\right)+0+4}{\sqrt{\left(1-a\right)^2+1+1}}\right|=\sqrt{3}\end{array} \)
\(\begin{array}{l} \Rightarrow 25 + a^2 – 10a = 3a^2 – 6a + 9\\ \Rightarrow 2a^2 + 4a – 16 = 0\\ \Rightarrow a^2 + 2a – 8 = 0\\ a = 2~ or -4\\ \therefore a_{max} = 2\end{array} \)
3. Numbers are to be formed between 1000 and 3000, which are divisible by 4, using the digits 1, 2, 3, 4, 5 and 6 without repetition of digits. Then the total number of such numbers is ______________.
Answer (30)
Sol. Number must start by 1 or 2 and for divisibility by
4 last two digits shall be divisible by 4

⇒ Total 30 numbers
4. If \(\begin{array}{l} \sum_{k=1}^{10}\frac{k}{k^4+k^2+1}=\frac{m}{n}\end{array} \)
, where m and n are co-prime, then m + n is equal to
Answer (166)
Sol.
\(\begin{array}{l} \sum_{k=1}^{10}\frac{k}{k^4+k^2+1}\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left[\sum_{k=1}^{10}\right.\left(\frac{1}{k^2-k+1}-\frac{1}{k^2+k+1}\right)\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left[1-\frac{1}{3}+\frac{1}{3}-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+\cdots+\frac{1}{91}-\frac{1}{111}\right]\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left[1-\frac{1}{111}\right]=\frac{110}{2.111}=\frac{55}{111}=\frac{m}{n}\end{array} \)
∴ m + n = 55 + 111 = 166
5. If the sum of solutions of the system of equations 2sin2θ – cos2θ = 0 and 2cos2θ + 3sinθ = 0 in the interval [0, 2π] is kπ, then k is equal to _______.
Answer (3)
Sol. Equation (1)
\(\begin{array}{l} 2sin^2\theta = 1 – 2sin^2\theta \end{array} \)
\(\begin{array}{l}\Rightarrow sin^2\theta = \frac{1}{4}\end{array} \)
\(\begin{array}{l} \Rightarrow \sin\theta=\pm\frac{1}{2}\end{array} \)
\(\begin{array}{l} \Rightarrow \theta=\frac{\pi}{6},\frac{5\pi}{6},\frac{7\pi}{6},\frac{11\pi}{6}\end{array} \)
\(\begin{array}{l} \text{Equation}(2)~2cos^2\theta + 3sin\theta = 0\\ \Rightarrow 2sin^2\theta – 3sin\theta – 2 = 0\\ \Rightarrow 2sin^2\theta – 4sin\theta + sin\theta – 2 = 0\\ \Rightarrow (sin\theta – 2) (2sin\theta + 1) = 0 \end{array} \)
\(\begin{array}{l} \Rightarrow \sin\theta=\frac{-1}{2}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \theta=\frac{7\pi}{6},\frac{11\pi}{6}\end{array} \)
\(\begin{array}{l} \therefore \text{Common solutions = } \frac{7\pi}{6};\frac{11\pi}{6}\end{array} \)
\(\begin{array}{l} \text{Sum of solutions =}\frac{7\pi+11\pi}{6}=\frac{18\pi}{6}=3\pi\\ \therefore k = 3\end{array} \)
6. The mean and standard deviation of 40 observations are 30 and 5 respectively. It was noticed that two of these observations 12 and 10 were wrongly recorded. If σ is the standard deviation of the data after omitting the two wrong observations from the data, then 38σ2 is equal to ______.
Answer (238)
Sol.
\(\begin{array}{l} \mu=\frac{\sum x_i}{40}=30\ \Rightarrow \sum x_i=1200\end{array} \)
\(\begin{array}{l} \sigma^2=\frac{\sum x_i^2}{40}-\left(30\right)^2=25\ \Rightarrow\ \sum x_i^2 = 37000\end{array} \)
After omitting two wrong observations
\(\begin{array}{l} \sum y_i=1200-12-10=1178\end{array} \)
\(\begin{array}{l} \sum y_i^2=37000-144-100=36756 \end{array} \)
Now
\(\begin{array}{l} \sigma^2=\frac{\sum y_i^2}{38}-\left(\frac{\sum y_i}{38}\right)^2\end{array} \)
\(\begin{array}{l} =\frac{36756}{38}-\left(\frac{1178}{38}\right)^2=-31^2\end{array} \)
\(\begin{array}{l} 38\sigma ^2 = 36756 – 36518 = 238\end{array} \)
7. The plane passing through the line L :lx – y + 3(1 – l) z = 1, x + 2y – z = 2 and perpendicular to the plane 3x + 2y + z = 6 is 3x – 8y + 7z = 4. If θ is the acute angle between the line L and the y-axis, then 415 cos2θ is equal to ________.
Answer (125)
Sol. L :lx – y + 3 (1 – l)z = 1, x + 2y – z = 2
and plane containing the line p : 3x – 8y + 7z = 4
Let
\(\begin{array}{l}\vec{n}\end{array} \)
be the vector parallel to L.
then
\(\begin{array}{l}\vec{n}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ l& -1 & 3\left(1-l\right) \\1 & 2 & -1 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l} =\left(6l-5\right)\hat{i}+\left(3-2l\right)\hat{j}+\left(2l+1\right)\hat{k}\end{array} \)
∵ R containing L
3(6l – 5) – 8(3 – 2l) + 7 (2l + 1) = 0
18l + 16l + 14l – 15 – 24 + 7 = 0
\(\begin{array}{l} \therefore l=\frac{32}{48}=\frac{2}{3} \end{array} \)
Let θ be the acute angle between L and y-axis
\(\begin{array}{l} \therefore\ \cos\theta=\frac{\frac{5}{3}}{\sqrt{1+\frac{25}{9}+\frac{49}{9}}}=\frac{5}{\sqrt{83}}\end{array} \)
\(\begin{array}{l} \therefore\ 415\cos^2\theta=125\end{array} \)
8. Suppose y = y(x) be the solution curve to the differential equation \(\begin{array}{l} \frac{dy}{dx}-y=2-e^{-x}\ \text{such that}\ \displaystyle \lim_{x \to \infty}y\left(x\right)\end{array} \)
is finite. If a and bare respectively the x – and y – intercepts of the tangent to the curve at x = 0, then the value of a – 4b is equal to _____.
Answer (3)
Sol.
\(\begin{array}{l}\text{If} = e^{-x}\\y\cdot e^{-x}=-2e^{-x}+\frac{e^{-2x}}{2}+C \end{array} \)
\(\begin{array}{l}\Rightarrow y = -2 + e^{-x}+Ce^x\\ \displaystyle \lim_{x \to \infty} y\left(x\right)\text{is finite so}~C = 0\end{array} \)
y = –2 + e–x
\(\begin{array}{l} \Rightarrow \underset{~~~~~~~~~~~~~~~~~~~~~~~x=0}{\left.\frac{dy}{dx}=-e^{-x}\Rightarrow \frac{dy}{dx}\right|} =-1\end{array} \)
Equation of tangent
y + 1 = –1 (x – 0)
or y + x = –1
Soa = –1, b = –1
⇒ a–4b = 3
9. Different A.P.’s are constructed with the first term 100, the last term 199, and integral common differences. The sum of the common differences of all such A.P.’s having at least 3 terms and at most 33 terms is ______.
Answer (53)
Sol.
\(\begin{array}{l} d_1=\frac{199-100}{2}\notin I\end{array} \)
\(\begin{array}{l} d_2=\frac{199-100}{3}=33\end{array} \)
\(\begin{array}{l} d_3=\frac{199-100}{4}\notin I\end{array} \)
\(\begin{array}{l} d_n=\frac{199-100}{i+1}\in I \end{array} \)
di= 33 + 11, 9
Sum of CD’s = 33 + 11 + 9
= 53
10. The number of matrices \(\begin{array}{l} A=\begin{pmatrix}a & b \\c & d \\\end{pmatrix},\ \text{where}\ a, b, c, d\in{-1, 0, 1, 2, 3, …..,10},\end{array} \)
such that A = A–1, is ______.
Answer (50)
Sol.
\(\begin{array}{l} \because\ A=\begin{bmatrix}a & b \\c & d \\\end{bmatrix}\text{ then }A^2=\begin{bmatrix}a^2+bc & b\left(a+d\right) \\c\left(a+d\right) & bc+d^2 \\\end{bmatrix}\end{array} \)
For A–1 must exist ad – bc≠ 0 …(i)
and A = A–1⇒A2 = I
∴ a2 + bc = d2 + bc = 1 …(ii)
and b(a + d) = c(a + d) = 0 …(iii)
Case I : When a = d = 0, then possible values of
(b, c) are (1, 1), (–1, 1) and (1, –1) and (–1, 1).
Total four matrices are possible.
Case II : When a = –d then (a, d) be (1, –1) or
(–1, 1).
Then total possible values of (b, c) are
(12 + 11) × 2 = 46.
∴ Total possible matrices = 46 + 4 = 50.
JEE Main 2022 July 26th Shift 2 Paper Analysis with Solutions
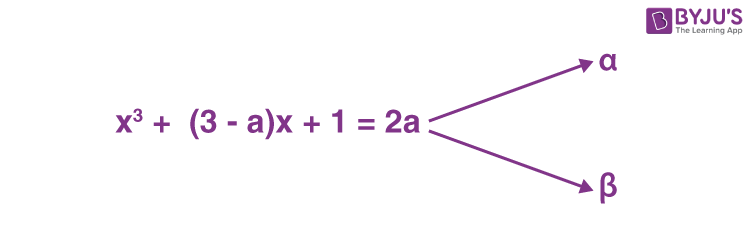












Comments