The JEE Main 2022 June 26 β Shift 2 Maths Question Paper with Solutions are given on this page. Students can view the JEE Main 2022 answer keys and find the correct answers. The JEE Main 2022 question paper with solutions help students to get to know the JEE Main 2022 exam pattern and marking scheme. Candidates are advised to study the JEE Main 2022 question paper with solutions, so that they can prepare well for other entrance exams too. They can also download the JEE Main 2022 June 26 β Shift 2 Maths Question Paper with Solutions in PDF format.
JEE Main 2022 26th June Evening Shift Maths Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let \(\begin{array}{l}f:\mathbb{R}\rightarrow \mathbb{R}\end{array} \)
be defined as f(x) = x β 1 and \(\begin{array}{l}g:\mathbb{R}-\left\{1,-1 \right\}\to \mathbb{R}\end{array} \)
be defined as\(\begin{array}{l}g(x)=\frac{x^2}{x^2-1}.\end{array} \)
Then the function fog is:
(A) One-one but not onto
(B) Onto but not one-one
(C) Both one-one and onto
(D) Neither one-one nor onto
Answer (D)
Sol.
\(\begin{array}{l}f:\mathbb{R}\to \mathbb{R}\end{array} \)
defined as
f(x) = x β 1 and g : ββ {1, β1} β β,
\(\begin{array}{l}g(x) = \frac{x^2}{x^2-1}\end{array} \)
Now fog(x)
\(\begin{array}{l}=\frac{x^2}{x^2-1}-1=\frac{1}{x^2-1}\end{array} \)
β΄ Domain of fog(x) = ββ {β1, 1}
And range of fog(x) = (ββ, β1] β (0, β)
Now,
\(\begin{array}{l}\frac{d}{dx}(fog(x))=\frac{-1}{(x^2-1)^2}.2x=\frac{2x}{(1-x^2)^2}\end{array} \)
\(\begin{array}{l}\therefore \frac{d}{dx}(fog(x))>0\ \text{for}\ \frac{2x}{\left((1-x)(1+x)\right )^2}>0\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x}{\left ((x-1)(x+1)\right )^2}<0\end{array} \)
\(\begin{array}{l}\therefore x\in (-\infty ,0)\end{array} \)
and
\(\begin{array}{l}\frac{d}{dx}(fog(x))<0\ \text{for}\ x\in (0,\infty)\end{array} \)
β΄ fog(x) is neither one-one nor onto.
2. If the system of equations Ξ±x + y + z = 5, x + 2y + 3z = 4, x + 3y +5z = Ξ² has infinitely many solutions, then the ordered pair (Ξ±, Ξ²) is equal to:
(A) (1, β3)
(B) (β1, 3)
(C) (1, 3)
(D) (β1, β3)
Answer (C)
Sol. Given system of equations
Ξ±x + y + z = 5
x + 2y + 3z = 4, has infinite solution
x + 3y + 5z = Ξ²
\(\begin{array}{l}\therefore \Delta =\begin{vmatrix}\alpha &1 &1 \\1 &2 &3 \\1 &3 &5 \\\end{vmatrix}=0 \end{array} \)
β Ξ±(1) β 1(2) + 1(1) = 0
β Ξ± = 1
and
\(\begin{array}{l}\Delta _1=\begin{vmatrix}5 &1 &1 \\4 &2 &3 \\\beta &3 &5 \\\end{vmatrix}=0\end{array} \)
β 5(1) β 1(20 β 3Ξ²) + 1(12 β 2Ξ²) = 0
β Ξ² = 3
And
\(\begin{array}{l}\Delta _2=\begin{vmatrix}1 &5 &1 \\1 &4 &3 \\1 &\beta &5 \\\end{vmatrix}=0\end{array} \)
β (20 β 3Ξ²) β 5(2) + 1(Ξ² β 4) = 0
β β2Ξ² + 6 = 0
β Ξ² = 3
Similarly,
\(\begin{array}{l}\Rightarrow \Delta _3=\begin{vmatrix}1 &1 &5 \\1 &2 &4 \\1 &3 &\beta \\\end{vmatrix}=0\end{array} \)
β Ξ² = 3
β΄ (Ξ±, Ξ²) = (1, 3)
3. \(\begin{array}{l}\text{If}\ A=\sum_{n=1 }^{\infty}\frac{1}{\left(3+(-1)^n\right)^n}\ \text{and}\ B=\sum_{n=1 }^{\infty}\frac{(-1)^n}{\left(3+(-1)^n\right)^n},\end{array} \)
then A/B is equal to:
(A) 11/9
(B) 1
(C) -11/9
(D) -11/3
Answer (C)
Sol.
\(\begin{array}{l}A=\sum_{n=1}^{\infty}\frac{1}{\left (3+(-1)^n\right )^n}\end{array} \)
and \(\begin{array}{l}B=\sum_{n=1}^{\infty}\frac{(-1)^n}{\left (3+(-1)^n\right )^n}\end{array} \)
\(\begin{array}{l}A=\frac{1}{2}+\frac{1}{4^2}+\frac{1}{2^3}+\frac{1}{4^4}+….\end{array} \)
\(\begin{array}{l}B=\frac{-1}{2}+\frac{1}{4^2}-\frac{1}{2^3}+\frac{1}{4^4}+….\end{array} \)
\(\begin{array}{l}A=\frac{\frac{1}{2}}{1-\frac{1}{4}}+\frac{\frac{1}{16}}{1-\frac{1}{16}},B=\frac{-\frac{1}{2}}{1-\frac{1}{4}}+\frac{\frac{1}{16}}{1-\frac{1}{16}}\end{array} \)
\(\begin{array}{l}A=\frac{11}{15},B=\frac{-9}{15}\end{array} \)
\(\begin{array}{l}\therefore \frac{A}{B}=\frac{-11}{9}\end{array} \)
4. \(\begin{array}{l}\displaystyle \lim_{x\to 0}\frac{cos(sin~x)-cos~x}{x^4}\ \text{is equal to}:\end{array} \)
(A) 1/3
(B) 1/4
(C) 1/6
(D) 1/12
Answer (C)
Sol.
\(\begin{array}{l}\displaystyle \lim_{x\to 0}\frac{cos(sin x)-cos x}{x^4}=\displaystyle \lim_{x\to 0}\frac{2sin(x+sin x).sin\left ( \frac{x-sin x}{2} \right )}{x^4}\end{array} \)
\(\begin{array}{l}=\displaystyle \lim_{x\to 0}2.\left ( \frac{\left ( \frac{x+sinx}{2} \right )\left ( \frac{x-sinx}{2} \right )}{x^4} \right )\end{array} \)
\(\begin{array}{l}=\displaystyle \lim_{x\to 0}\frac{1}{2}.\left ( \frac{\left ( x+x-\frac{x^3}{3!}+\frac{x^5}{5!}…. \right )\left ( x-x+\frac{x^3}{3!}…\right )}{x^4} \right )\end{array} \)
\(\begin{array}{l}=\displaystyle \lim_{x\to 0}\frac{1}{2}.\left ( 2-\frac{x^2}{3!}+\frac{x^4}{5!}….\right)\left (\frac{1}{3!}-\frac{x^2}{5!}-1\right)\end{array} \)
\(\begin{array}{l}=\frac{1}{6}\end{array} \)
5. Let f(x) = min {1, 1 + x sin x}, 0 β€ x β€ 2Ο. If m is the number of points, where f is not differentiable, and n is the number of points, where f is not continuous, then the ordered pair (m, n) is equal to
(A) (2, 0)
(B) (1, 0)
(C) (1, 1)
(D) (2, 1)
Answer (B)
Sol. f(x) = min{1, 1 + xsinx}, 0 β€x β€2Ο
\(\begin{array}{l}f(x)=\left\{\begin{matrix}1, 0\leq x<\pi& \\1+xsinx, \pi\leq x\leq 2\pi &\\\end{matrix}\right.\end{array} \)
Now at x = Ο,
\(\begin{array}{l}\displaystyle \lim_{x \to \pi^-}f(x)=1=\displaystyle \lim_{x \to \pi^+}f(x)\end{array} \)
β΄ f(x) is continuous in [0, 2Ο]
Now, at x = Ο
\(\begin{array}{l}L.H.D = \displaystyle \lim_{h\to 0}\frac{f(\pi-h)-f(\pi)}{-h}=0\end{array} \)
\(\begin{array}{l}R.H.D. =\displaystyle \lim_{h\to 0}\frac{f(\pi+h)-f(\pi)}{-h}=1-\frac{(\pi+h)sinh-1}{h}\end{array} \)
= βΟ
β΄ f(x) is not differentiable at x = Ο
β΄ (m, n) = (1, 0)
6. Consider a cuboid of sides 2x, 4x and 5x and a closed hemisphere of radius r. If the sum of their surface areas is a constant k, then the ratio x : r, for which the sum of their volumes is maximum, is
(A) 2 : 5
(B) 19 : 45
(C) 3 : 8
(D) 19 : 15
Answer (B)
Sol.
\(\begin{array}{l}\because s_1+s_2=k\end{array} \)
\(\begin{array}{l}76x^2+3\pi r^2=k\end{array} \)
\(\begin{array}{l}\therefore 152x\frac{dx}{dr}+6\pi r=0\end{array} \)
\(\begin{array}{l}\therefore \frac{dx}{dr}=\frac{-6\pi r}{152x}\end{array} \)
Now
\(\begin{array}{l}V=40x^3+\frac{2}{3}\pi r^3\end{array} \)
\(\begin{array}{l}\therefore \frac{dv}{dr}=120x^2.\frac{dx}{dr}+2\pi r^2=0\end{array} \)
\(\begin{array}{l}\Rightarrow 120x^2.\left ( \frac{-6\pi}{152}\frac{r}{x}\right)+2\pi r^2=0\end{array} \)
\(\begin{array}{l}\Rightarrow 120\left ( \frac{x}{r}\right)=2\pi\left ( \frac{152}{6\pi} \right )\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( \frac{x}{r}\right)=\frac{152}{3}\frac{1}{120}=\frac{19}{45}\end{array} \)
7. The area of the region bounded by y2 = 8x and y2 = 16(3 β x) is equal to
\(\begin{array}{l}(A)\ \frac{32}{3}\end{array} \)
\(\begin{array}{l}(B)\ \frac{40}{3}\end{array} \)
(C) 16
(D) 19
Answer (C)
Sol.
\(\begin{array}{l}c_1:y^2=8x\end{array} \)
\(\begin{array}{l}c_2:y^2=16(3-x)\end{array} \)
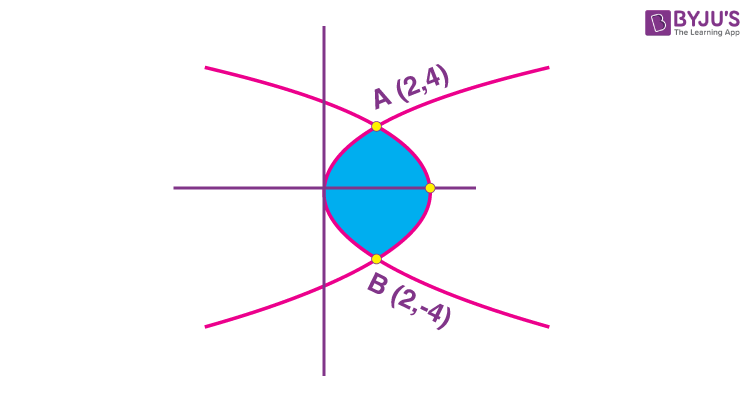
Solving c1 and c2
48 β 16x = 8x
x = 2
β΄ y = Β± 4
β΄ Area of shaded region
\(\begin{array}{l}=2\int_{0}^{4}\left\{\left ( \frac{48-y^2}{16}\right )-\left ( \frac{y^2}{8}\right)\right\}dy\end{array} \)
\(\begin{array}{l}=\frac{1}{8}\left [ 48y-y^3\right]_{0}^{4}=16\end{array} \)
8. \(\begin{array}{l}\text{If}\ \int\frac{1}{x}\sqrt{\frac{1-x}{1+x}}dx=g(x)+c,g(1)=0,\ \text{then}\ g\left(\frac{1}{2}\right )\end{array} \)
is equal to
\(\begin{array}{l}(A)\ log_e\left(\frac{\sqrt{3}-1}{\sqrt{3}+1}\right)+\frac{\pi}{3}\end{array} \)
\(\begin{array}{l}(B)\ log_e\left(\frac{\sqrt{3}+1}{\sqrt{3}-1}\right)+\frac{\pi}{3}\end{array} \)
\(\begin{array}{l}(C)\ log_e\left(\frac{\sqrt{3}+1}{\sqrt{3}-1}\right)-\frac{\pi}{3}\end{array} \)
\(\begin{array}{l}(D)\ \frac{1}{2}log_e\left(\frac{\sqrt{3}-1}{\sqrt{3}+1}\right)-\frac{\pi}{6}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}\because \int \frac{1}{x}\sqrt{\frac{1-x}{1+x}}dx=g(x)+c \end{array} \)
\(\begin{array}{l}\int_{1}^{\frac{1}{2}}\frac{1}{x}\sqrt{\frac{1-x}{1+x}}dx=g\left(\frac{1}{2}\right)-g(1)\end{array} \)
\(\begin{array}{l}\therefore g\left(\frac{1}{2}\right)=\int_{1}^{\frac{1}{2}}\frac{1}{x}\sqrt{\frac{1-x}{1+x}}dx \end{array} \)
\(\begin{array}{l}cotx=cos2\theta\end{array} \)
\(\begin{array}{l}=\int_{0}^{\frac{\pi}{6}}\frac{1}{cos2\theta}.\frac{sin\theta}{cos\theta}(-2sin2\theta)d\theta\end{array} \)
\(\begin{array}{l}=-\int_{0}^{\frac{\pi}{6}}\frac{4sin^2\theta}{cos2\theta}d\theta\end{array} \)
\(\begin{array}{l}=2\int_{0}^{\frac{\pi}{6}}\frac{(1-2sin^2\theta)-1}{cos2\theta}d\theta\end{array} \)
\(\begin{array}{l}=2\int_{0}^{\frac{\pi}{6}}(1-sec2\theta)d\theta\end{array} \)
\(\begin{array}{l}=\frac{\pi}{3}-2.\frac{1}{2}[In\left|sec2\theta+tan 2\theta\right|]_{0}^{\frac{\pi}{6}}\end{array} \)
\(\begin{array}{l}=\frac{\pi}{3}-\left [In\left|2+\sqrt{3}\right|-In1\right]\end{array} \)
\(\begin{array}{l}=\frac{\pi}{3}+In\left(\frac{1}{2+\sqrt{3}}\right)\end{array} \)
\(\begin{array}{l}=\frac{\pi}{3}+In\left|\frac{\sqrt{3}-1}{\sqrt{3}+1} \right|\end{array} \)
9. If y = y(x) is the solution of the differential equation \(\begin{array}{l}x\frac{dy}{dx}+2y=xe^x,y(1)=0\end{array} \)
then the local maximum value of the function \(\begin{array}{l}z(x)=x^2y(x)-e^x,x\in R\end{array} \)
is
(A) 1 β e
(B) 0
(C) 1/2
\(\begin{array}{l}(D)\ \frac{4}{e}-e\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}x\frac{dy}{dx}+2y=xe^x,y(1)=0\end{array} \)
\(\begin{array}{l}\frac{dy}{dx}+\frac{2}{x}y=e^x,\ \text{then}\ e^{\int \frac{2}{x}dx}dx=x^2\end{array} \)
\(\begin{array}{l}y.x^2=\int x^2e^xdx\end{array} \)
\(\begin{array}{l}yx^2=x^2e^x-\int 2xe^xdx\end{array} \)
\(\begin{array}{l}=x^2e^x-2(xe^x-e^x)+c\end{array} \)
\(\begin{array}{l}yx^2=x^2e^x-2xe^x+2e^x+c\end{array} \)
\(\begin{array}{l}yx^2=(x^2-2x+2)e^x+c\end{array} \)
\(\begin{array}{l}0=e+c\Rightarrow c=-e\end{array} \)
\(\begin{array}{l}y(x).x^2-e^x=(x-1)^2e^x-e\end{array} \)
\(\begin{array}{l}z(x)=(x-1)^2e^x-e\end{array} \)
For local maximum z'(x) = 0
\(\begin{array}{l}\therefore 2(x-1)e^x +(x-1)^2e^x=0\end{array} \)
β΄ x = β1
And local maximum value = z(-1)
\(\begin{array}{l}=\frac{4}{e}-e\end{array} \)
10. If the solution of the differential equation \(\begin{array}{l}\frac{dy}{dx}+e^x(x^2-2)y=(x^2-2x)(x^2-2)e^{2x}\end{array} \)
satisfies y(0) = 0, then the value of y(2) is ______.
(A) β1
(B) 1
(C) 0
(D) e
Answer (C)
Sol.
\(\begin{array}{l}\because \frac{dy}{dx}+e^x(x^2-2)y=(x^2-2x)(x^2-2)e^{2x}\end{array} \)
Here, I.F.
\(\begin{array}{l}=e^{\int e^x(x^2-2)dx}\end{array} \)
\(\begin{array}{l}=e^{(x^2-2x)e^x}\end{array} \)
β΄ Solution of the differential equation is
\(\begin{array}{l}y.e^{(x^2-2x)e^x}=\int (x^2-2x)(x^2-2)e^{2x}.e^{(x^2-2x)e^x}dx\end{array} \)
\(\begin{array}{l}=\int (x^2-2x)e^x.(x^2-2)e^x.e^{(x^2-2x)e^x}dx\end{array} \)
Let
\(\begin{array}{l}(x^2-2x)e^x=t\end{array} \)
\(\begin{array}{l}\therefore (x^2-2)e^xdx=dt\end{array} \)
\(\begin{array}{l}y.e^{(x^2-2x)e^x}=\int t.e^tdt\end{array} \)
\(\begin{array}{l}y.e^{(x^2-2x)e^x}=(x^2-2x-1)e^{(x^2-2x)e^x}+c\end{array} \)
β΄ y(0) = 0
β΄ c = 1
\(\begin{array}{l}\therefore y=(x^2-2x-1)+e^{(2x-x^2)e^x} \end{array} \)
β΄ y(2) = β1 + 1 = 0
11. If m is the slope of a common tangent to the curves \(\begin{array}{l}\frac{x^2}{16}+\frac{y^2}{9}=1\end{array} \)
and x2 + y2 = 12, then 12m2 is equal to:
(A) 6
(B) 9
(C) 10
(D) 12
Answer (B)
Sol.
\(\begin{array}{l}C_1:\frac{x^2}{16}+\frac{y^2}{9}=1\end{array} \)
and \(\begin{array}{l}C_2:x^2+y^2=12\end{array} \)
Let
\(\begin{array}{l}y=mx\pm \sqrt{16m^2+9}\end{array} \)
be any tangent to C1 and if this is also tangent to C2 then
\(\begin{array}{l}\left|\frac{\sqrt{16m^2+9}}{\sqrt{m^2+1}}\right|=\sqrt{12}\end{array} \)
\(\begin{array}{l}\Rightarrow 16m^2+9=12m^2+12\end{array} \)
\(\begin{array}{l}\Rightarrow 4m^2=3\Rightarrow 12m^2=9\end{array} \)
12. The locus of the mid-point of the line segment joining the point (4, 3) and the points on the ellipse x2 + 2y2 = 4 is an ellipse with eccentricity:
\(\begin{array}{l}(A)\ \frac{\sqrt{3}}{2}\end{array} \)
\(\begin{array}{l}(B)\ \frac{1}{2\sqrt{2}}\end{array} \)
\(\begin{array}{l}(C)\ \frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}(D)\ \frac{1}{2}\end{array} \)
Answer (C)
Sol. Let
\(\begin{array}{l}\text{Let}\ P(2cos\theta,\sqrt{2}sin\theta)\ \text{be any point on ellipse}\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array} \)
Β and Q(4, 3) and let (h, k) be the mid point of PQ then
\(\begin{array}{l}h=\frac{2cos\theta+4}{2},k=\frac{\sqrt{2}sin\theta+3}{2}\end{array} \)
\(\begin{array}{l}\therefore cos\theta=h-2,sin\theta=\frac{2k-3}{\sqrt{2}} \end{array} \)
\(\begin{array}{l}\therefore (h-2)^2+\left(\frac{2k-3}{\sqrt{2}}\right)^2=1\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{(x-2)^2}{1}+\frac{\left(y-\frac{3}{2}\right)^2}{\frac{1}{2}}=1\end{array} \)
\(\begin{array}{l}\therefore e=\sqrt{1-\frac{1}{2}}=\frac{1}{\sqrt{2}} \end{array} \)
13. The normal to the hyperbola \(\begin{array}{l}\frac{x^2}{a^2}-\frac{y^2}{9}=1\end{array} \)
at the point (8, 3β3)Β on it passes through the point:
\(\begin{array}{l}(A)\ (15,-2\sqrt{3})\end{array} \)
\(\begin{array}{l}(B)\ (9,2\sqrt{3})\end{array} \)
\(\begin{array}{l}(C)\ (-1,9\sqrt{3})\end{array} \)
\(\begin{array}{l}(D)\ (-1,6\sqrt{3})\end{array} \)
Answer (C)
Sol. Given hyperbola :
\(\begin{array}{l}\frac{x^2}{a^2}-\frac{y^2}{9}=1\end{array} \)
β΅ It passes through
\(\begin{array}{l}(8,3\sqrt{3})\end{array} \)
\(\begin{array}{l}\because \frac{64}{a^2}-\frac{27}{9}=1\Rightarrow a^2=16\end{array} \)
Now, equation of normal to hyperbola
\(\begin{array}{l}\frac{16x}{8}+\frac{9y}{3\sqrt{3}}=16+9\end{array} \)
\(\begin{array}{l}\Rightarrow 2x+\sqrt{3}y=25….(i)\end{array} \)
(-1, 9β3)Β satisfies (i)
14. If the plane 2x + y β 5z = 0 is rotated about its line of intersection with the plane 3x β y + 4z β 7 = 0 by an angle of Ο/2, then the plane after the rotation passes through the point:
(A) (2, β2, 0)
(B) (β2, 2, 0)
(C) (1, 0, 2)
(D) (β1, 0, β2)
Answer (C)
Sol. P1 : 2x + y β 52 = 0, P2 : 3x β y + 4z β 7 = 0
Family of planes P1 and P2
\(\begin{array}{l}P:P_1+\lambda P_2\end{array} \)
\(\begin{array}{l}\therefore P:(2+3\lambda)x+(1-\lambda)y+(-5+4\lambda)z-7\lambda=0 \end{array} \)
\(\begin{array}{l}\because P\perp P_1 \therefore 4+6\lambda+1-\lambda+25-20\lambda=0 \end{array} \)
\(\begin{array}{l}\lambda=2\end{array} \)
β΄ P : 8x β y + 32 β 14 = 0
It passes through the point (1, 0, 2).
15. If the lines \(\begin{array}{l}\vec{r}=(\hat{i}-\hat{j}+\hat{k})+\lambda (3\hat{j}-\hat{k})\end{array} \)
and \(\begin{array}{l}\vec{r}=(\alpha \hat{i}-\hat{j})+\mu(2\hat{j}-3\hat{k})\end{array} \)
are co-planar, then the distance of the plane containing these two lines from the point (Ξ±, 0, 0) is :
\(\begin{array}{l}(A)\ \frac{2}{9}\end{array} \)
\(\begin{array}{l}(B)\ \frac{2}{11}\end{array} \)
\(\begin{array}{l}(C)\ \frac{4}{11}\end{array} \)
(D) 2
Answer (B)
Sol. β΅ Both lines are coplanar, so
\(\begin{array}{l}\begin{vmatrix}\alpha -1 &0 &-1 \\0 &3 &-1 \\2 &0 &-3 \\\end{vmatrix}=0\end{array} \)
\(\begin{array}{l}\Rightarrow \alpha=\frac{5}{3}\end{array} \)
Equation of plane containing both lines
\(\begin{array}{l}\begin{vmatrix}x-1 &y+1 &z-1 \\0 &3 &-1 \\2 &0 &-3 \\\end{vmatrix}=0\end{array} \)
β 9x + 2y + 6z = 13
So, distance of (5/3, 0, 0) from this plane
\(\begin{array}{l}=\frac{2}{\sqrt{81+4+36}}=\frac{2}{11}\end{array} \)
16. Let \(\begin{array}{l}\vec{a}=\hat{i}+\hat{j}+2\hat{k},\vec{b}=2\dot{i}-3\hat{j}+\hat{k}\end{array} \)
and \(\begin{array}{l}\vec{c}=\hat{i}-\hat{j}+\hat{k}\end{array} \)
be three given vectors. \(\begin{array}{l}\text{Let}\ \vec{v}\ \text{be a vector in the plane of}\ \vec{a}\ \text{and}\ \vec{b}\ \text{whose projection on}\ \vec{c}\ \text{is}\ \frac{2}{\sqrt{3}}.\end{array} \)
\(\begin{array}{l}\text{If}\ \vec{v}.\hat{j}=7,\ \text{then}\ \vec{v}.(\hat{i}+\hat{k})\ \text{is equal to}:\end{array} \)
(A) 6
(B) 7
(C) 8
(D) 9
Answer (D)
Sol. Let
\(\begin{array}{l}\vec{v}=\lambda_1\vec{a}+\lambda_2\vec{b}, \end{array} \)
where Ξ»1, Ξ»2 β β.
\(\begin{array}{l}=(\lambda_1+2\lambda_2)\hat{i}+(\lambda_1-3\lambda_2)\hat{j}+(2\lambda_1+\lambda_2)\hat{k} \end{array} \)
\(\begin{array}{l}\because \text{Projection of}\ \vec{v}\ \text{on}\ \vec{c}\ \text{is}\ \frac{2}{\sqrt{3}}\end{array} \)
\(\begin{array}{l}\therefore \frac{\lambda_1+2\lambda_2-\lambda_1+3\lambda_2+2\lambda_1+\lambda_2}{\sqrt{3}}=\frac{2}{\sqrt{3}}\end{array} \)
\(\begin{array}{l}\therefore \lambda_1+3\lambda_2=1…..(i)\end{array} \)
and
\(\begin{array}{l}\vec{v}.\hat{j}=7\Rightarrow \lambda_1-3\lambda_2=7…..(ii) \end{array} \)
from equation (i) and (ii)
Ξ»1 = 4, Ξ»2 = β 1
\(\begin{array}{l}\therefore \vec{v}=2\hat{i}+7\hat{j}+7\hat{k} \end{array} \)
\(\begin{array}{l}\therefore \vec{v}.(\hat{i}+\hat{k})=2+7\end{array} \)
= 9
17. The mean and standard deviation of 50 observations are 15 and 2 respectively. It was found that one incorrect observation was taken such that the sum of correct and incorrect observations is 70. If the correct mean is 16, then the correct variance is equal to :
(A) 10
(B) 36
(C) 43
(D) 60
Answer (C)
Sol. Given
\(\begin{array}{l}\bar{x}=15,\sigma =2\Rightarrow \sigma^2=4 \end{array} \)
β΄ x2 + x2 + β¦β¦ + x50 = 15 Γ 50 = 750
\(\begin{array}{l}4=\frac{x_{1}^{2}+x_{2}^{2}….+x_{50}^{2}}{50}-225\end{array} \)
\(\begin{array}{l}\therefore x_{1}^{2}+x_{2}^{2}+….+x_{50}^{2}=50\times229 \end{array} \)
Let a be the correct observation and b is the incorrect observation then a + b = 70
and
\(\begin{array}{l}16=\frac{75-b+a}{50}\end{array} \)
β΄ a β b = 50 β a = 60, b = 10
β΄ Correct variance
\(\begin{array}{l}=\frac{50\times229+60^2-10^2}{50}-256\end{array} \)
= 43
18. 16 sin(20Β°) sin(40Β°) sin(80Β°) is equal to :
(A) β3
(B) 2β3
(C) 3
(D) 4β3
Answer (B)
Sol.16 sin20Β° Β· sin40Β° Β· sin80Β°
= 4sin60Β° {β΅ 4sinΞΈβ
sin(60Β° β ΞΈ)β
sin(60Β° + ΞΈ) = sin3ΞΈ }
\(\begin{array}{l}=2\sqrt{3}\end{array} \)
19. If the inverse trigonometric functions take principal values, then \(\begin{array}{l}cos^{-1}\left(\frac{3}{10}cos\left(tan^{-1}\left(\frac{4}{3}\right )\right )+\frac{2}{5}sin\left ( \tan^{-1}\left (\frac{4}{3} \right ) \right ) \right )\end{array} \)
is equal to :
(A) 0
\(\begin{array}{l}(B)\ \frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\pi}{3}\end{array} \)
\(\begin{array}{l}(D)\ \frac{\pi}{6}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}cos^{-1}\left ( \frac{3}{10}cos\left ( tan^{-1}\left ( \frac{4}{3} \right ) \right )+\frac{2}{5}sin\left ( tan^{-1}\left ( \frac{4}{3} \right ) \right ) \right )\end{array} \)
\(\begin{array}{l}=cos^{-1}\left ( \frac{3}{10}.\frac{3}{5}+\frac{2}{5}.\frac{4}{5}\right)\end{array} \)
\(\begin{array}{l}=cos^{-1}\left(\frac{1}{2}\right)=\frac{\pi}{3}\end{array} \)
20. Let r β {p, q, ~p, ~q} be such that the logical statement r β¨ (~p) β (p β§ q) β¨ r is a tautology. Then r is equal to :
(A) p
(B) q
(C) ~p
(D) ~q
Answer (C)
Sol. Clearly r must be equal to ~ p
β΅ ~ p β¨ ~ p = ~ p
and (p β§ q) β¨ ~ p = p
β΄ ~ p β p = tautology.
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, β00.33, β00.30, 30.27, β27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let f: β β βΒ satisfy f(x + y) = 2x f(y) + 4y f(x), β x, yβΒ β. If f(2) = 3, then 14. f'(4)/f'(2) is equal to ___.
Answer (248)
Sol. β΅ f(x + y) = 2x f(y) + 4y f(x) β¦(1)
Now, f(y + x) 2y f(x) + 4x f(y) β¦(2)
β΄ 2x f(y) + 4y f(x) = 2y f(x) + 4x f(y)
(4y β 2y) f(x) = (4x β 2x) f(y)
\(\begin{array}{l}\frac{f(x)}{4^x-2^x}=\frac{f(y)}{4^y-2^y}=k(Say)\end{array} \)
β΄ f(x) = k(4x β 2x)
β΅ f(2) = 3 then
\(\begin{array}{l}k=\frac{1}{4}\end{array} \)
\(\begin{array}{l}\therefore f(x)=\frac{4^x-2^x}{4}\end{array} \)
\(\begin{array}{l}\therefore fβ(x) = \frac{4^xIn4-2^xIn2}{4}\end{array} \)
\(\begin{array}{l}f'{(x)}=\frac{(2.4^x-2^x)In2}{4}\end{array} \)
\(\begin{array}{l}\therefore \frac{f'(4)}{f'(2)}=\frac{2.256-16}{2.16-4}\end{array} \)
\(\begin{array}{l}\therefore 14\frac{f'(4)}{f'(2)}=248\end{array} \)
2. Let p and q be two real numbers such that p + q = 3 and p4 + q4 = 369. Then \(\begin{array}{l}\left (\frac{1}{p}+\frac{1}{q}\right)^{-2}\end{array} \)
is equal to _______.
Answer (4)
Sol. β΅ p + q = 3 β¦(i)
and p4 + q4 = 369 β¦(ii)
{(p + q)2 β 2pq}2 β 2p2q2 = 369
or (9 β 2pq)2 β 2(pq)2 = 369
or (pq)2 β 18pq β 144 = 0
β΄ pq = β6 or 24
But pq = 24 is not possible
β΄ pq = β6
Hence,
\(\begin{array}{l}\left (\frac{1}{p}+\frac{1}{q}\right)^{-2}=\left ( \frac{pq}{p+q}\right)^2=(-2)^2=4\end{array} \)
3. If z2 + z + 1 = 0, \(\begin{array}{l}z\in \mathbb{C} ,\ \text{then}\ \left|\sum_{n=1}^{15}\left(z^n+(-1)^n\frac{1}{z^n}\right)^2\right|\end{array} \)
is equal to ________.
Answer (2)
Sol. β΅ z2 + z + 1 = 0 β Ο or Ο2
\(\begin{array}{l}\because \left|\sum_{n=1}^{15}\left(z^n+(-1)^n\frac{1}{z^n}\right)^2\right|\end{array} \)
\(\begin{array}{l}=\left|\sum_{n=1}^{15}z^{2n}+\sum_{n=1}^{15}z^{-2n}+2.\sum_{n=1}^{15}(-1)^{n}\right|\end{array} \)
= |0 + 0 β 2|
= 2
4. \(\begin{array}{l}\text{Let}\ X=\begin{bmatrix}0 &1 &0 \\0 &0 &1 \\0 &0 &0 \\\end{bmatrix},\end{array} \)
Y = Ξ±I + Ξ²X + Ξ³X2 and \(\begin{array}{l}Z=\alpha ^2l-\alpha\beta X+(\beta ^2-\alpha \gamma )X^2,\alpha,\beta,\gamma\in \mathbb{R} . \end{array} \)
\(\begin{array}{l}\text{If}\ Y^{-1}=\begin{bmatrix}\frac{1}{5} &\frac{-2}{5} &\frac{1}{5} \\0 &\frac{1}{5} &\frac{-2}{5} \\0 &0 &\frac{1}{5} \\\end{bmatrix}, \end{array} \)
then (Ξ± β Ξ² + Ξ³)2 is equal to ___________.
Answer (100)
Sol.
\(\begin{array}{l}\because X=\begin{bmatrix}0 &1 &0 \\0 &0 &1 \\0 &0 &0 \\\end{bmatrix} \end{array} \)
\(\begin{array}{l}\therefore X^2=\begin{bmatrix}0 &0 &1 \\0 &0 &0 \\0 &0 &0 \\\end{bmatrix} \end{array} \)
\(\begin{array}{l}\therefore Y=\alpha l+\beta X+\gamma X^2=\begin{bmatrix}\alpha &\beta &\gamma \\0 &\alpha &\beta \\0 &0 &\alpha \\\end{bmatrix} \end{array} \)
β΅ Y Β· Yβ1 = I
\(\begin{array}{l}\therefore\begin{bmatrix}\alpha &\beta &\gamma \\0 &\alpha &\beta \\0 &0 &\alpha \\\end{bmatrix}\begin{bmatrix}\frac{1}{5} &\frac{-2}{5} &\frac{1}{5} \\0 &\frac{1}{5} &\frac{-2}{5} \\0 &0 &\frac{1}{5} \\\end{bmatrix}=\begin{bmatrix}1 &0 &0 \\0 &1 &0 \\0 &0 &1 \\\end{bmatrix} \end{array} \)
\(\begin{array}{l}\therefore \begin{bmatrix}\frac{\alpha }{5} &\frac{\beta -2\alpha }{5} &\frac{\alpha -2\beta +\gamma }{5} \\0 &\frac{\alpha }{5} &\frac{\beta -2\alpha }{5} \\0 &0 &\frac{\alpha }{5} \\\end{bmatrix}=\begin{bmatrix}0 &0 &0 \\0 &1 &0 \\0 &0 &1 \\\end{bmatrix} \end{array} \)
β΄ Ξ± = 5, Ξ² = 10, Ξ³ = 15
β΄ (Ξ± – Ξ² + Ξ³)2 = 100
5. The total number of 3-digit numbers, whose greatest common divisor with 36 is 2, is _______.
Answer (150)
Sol. β΅ x β [100, 999], x β N
Then
\(\begin{array}{l}\frac{x}{2}\in [50,499],\ \frac{x}{2}\in N\end{array} \)
Number whose G.C.D with 18 is 1 in this range have the required condition. There are 6 such number from 18 Γ 3 to 18 Γ 4. Similarly from 18 Γ 4 to 18 Γ 5β¦.., 26 Γ 18 to 27 Γ 18
β΄ Total numbers = 24 Γ 6 + 6 = 150
The extra numbers are 53, 487, 491, 493, 497 and 499.
6. If \(\begin{array}{l}(^{40}C_0)+(^{41}C_1)+(^{42}C_2)+….+(^{60}C_{20})\frac{m}{n}~ ^{60}C_{20}\end{array} \)
m and n are coprime, then m + n is equal to _____.
Answer (102)
Sol.
\(\begin{array}{l}^{40}C_0+^{41}C_1+^{42}C_2+….+^{60}C_{20}\end{array} \)
\(\begin{array}{l}=^{40}C_{40}+^{41}C_{40}+^{42}C_{40}+….+^{60}C_{40}\end{array} \)
\(\begin{array}{l}=^{61}C_{41}\end{array} \)
\(\begin{array}{l}=\frac{61}{41}.^{60}C_{41}\end{array} \)
β΄ m = 61, n = 41
β΄ m + n = 102
7. If a1 (> 0), a2, a3, a4, a5 are in a G.P., a2 + a4 = 2a3 + 1 and 3a2 + a3 = 2a4, then a2 + a4 + 2a5 is equal to _______.
Answer (40)
Sol. Let G.P. be a1 = a, a2 = ar, a3 = ar2, β¦β¦
\(\begin{array}{l}\because 3a_2+a_3=2a_4 \end{array} \)
\(\begin{array}{l}\Rightarrow 3ar+ar^2=2ar^3 \end{array} \)
\(\begin{array}{l}\Rightarrow 2ar^2-r-3=0\end{array} \)
\(\begin{array}{l}\therefore r=-1 or \frac{3}{2} \end{array} \)
\(\begin{array}{l}\because a_1=a>0\ then\ r\neq -1 \end{array} \)
Now,
\(\begin{array}{l}a_2+a_4=2a_3+1\end{array} \)
\(\begin{array}{l}ar+ar^3=2ar^2+1\end{array} \)
\(\begin{array}{l}a\left ( \frac{3}{2}+\frac{27}{8}-\frac{9}{2}\right )=1\end{array} \)
\(\begin{array}{l}\therefore a=\frac{8}{3} \end{array} \)
\(\begin{array}{l}\therefore a_2+a_4+2a_5=a(r+r^3+2r^4)\end{array} \)
\(\begin{array}{l}=\frac{8}{3}\left(\frac{3}{2}+\frac{27}{8}+\frac{81}{8}\right)\end{array} \)
= 40
8. The integral \(\begin{array}{l}\frac{24}{\pi}\int_{0}^{\sqrt{2}}\frac{(2-x^2)dx}{(2+x^2)\sqrt{4+x^4}}\end{array} \)
is equal to _______.
Answer (3)
Sol.
\(\begin{array}{l}I=\frac{24}{\pi}\int_{0}^{\sqrt{2}}\frac{2-x^2}{(2+x^2)\sqrt{4+x^4}}dx\end{array} \)
Let
\(\begin{array}{l}x=\sqrt{2}t\Rightarrow dx=\sqrt{2}dt\end{array} \)
\(\begin{array}{l}I=\frac{24}{\pi}\int_{0}^{1}\frac{(2-2t^2).\sqrt{2}dt}{(2+2t^2)\sqrt{4+4t^4}}\end{array} \)
\(\begin{array}{l}=\frac{12\sqrt{2}}{\pi}\int_{0}^{1}\frac{\left(\frac{1}{t^2}-1\right)dt}{\left(t+\frac{1}{t}\right)\sqrt{\left(t+\frac{1}{t}\right)^2-2}}\end{array} \)
Let
\(\begin{array}{l}t+\frac{1}{t}=u\end{array} \)
\(\begin{array}{l}\Rightarrow \left(1-\frac{1}{t^2}\right)dt=du\end{array} \)
\(\begin{array}{l}=\frac{12\sqrt{2}}{\pi}\int_{\infty}^{2}\frac{-du}{u\sqrt{4^2-2}}\end{array} \)
\(\begin{array}{l}=\frac{12\sqrt{2}}{\pi}\int_{2}^{\infty}\frac{du}{u^2\sqrt{-\left(\frac{\sqrt{2}}{u}\right)^2}}\end{array} \)
\(\begin{array}{l}=\frac{12\sqrt{2}}{\pi}\int_{\frac{1}{\sqrt{2}}}^{0}\frac{-\frac{1}{\sqrt{2}}dp}{\sqrt{1-p^2}}\end{array} \)
\(\begin{array}{l}=\frac{12}{\pi}\left[sin^{-1}p\right]_{0}^{\frac{1}{\sqrt{2}}}\end{array} \)
\(\begin{array}{l}=\frac{12}{\pi}.\frac{\pi}{4}\end{array} \)
= 3
9. Let a line L1 be tangent to the hyperbola \(\begin{array}{l}\frac{x^2}{16}-\frac{y^2}{4}=1\end{array} \)
and let L2 be the line passing through the origin and perpendicular to L1. If the locus of the point of intersection of L1 and L2 is \(\begin{array}{l}(x^2+y^2)^2=\alpha x^2+\beta y^2,\end{array} \)
then Ξ± + Ξ² is equal to___.
Answer (12)
Sol. Equation of L1 is
\(\begin{array}{l}\frac{xsec\theta}{4}-\frac{ytan\theta}{2}=1…..(i)\end{array} \)
Equation of line L2 is
\(\begin{array}{l}\frac{x~tan\theta}{2}+\frac{y~sec\theta}{4}=0…..(ii)\end{array} \)
β΅ Required point of intersection of L1 and L2 is (x1, y1) then
\(\begin{array}{l}\frac{x_1sec\theta}{4}-\frac{y_1tan\theta}{2}-1=0…..(iii)\end{array} \)
and \(\begin{array}{l}\frac{y_1sec\theta}{4}+\frac{x_1tan\theta}{2}=0…..(iv)\end{array} \)
From equations (iii) and (iv)
\(\begin{array}{l}sec\theta=\frac{4x_1}{x_{1}^{2}+y_{1}^{2}}\ \text{and}\ tan\theta=\frac{-2y_1}{x_{1}^{2}+y_{1}^{2}}\end{array} \)
β΄ Required locus of (x1, y1) is
\(\begin{array}{l}(x^2+y^2)^2=16x^2-4y^2\end{array} \)
\(\begin{array}{l}\therefore \alpha =16,\beta =-4 \end{array} \)
\(\begin{array}{l}\therefore \alpha+\beta=12 \end{array} \)
10. If the probability that a randomly chosen 6-digit number formed by using digits 1 and 8 only is a multiple of 21 is p, then 96 p is equal to ________ .
Answer (33)
Sol. Total number of numbers from given
Condition = n(s) = 26.
Every required number is of the form
\(\begin{array}{l}A=7.(10^{a_{1}}+10^{a_{2}}+10^{a_{3}}+….)+111111\end{array} \)
Here 111111 is always divisible by 21.
β΄ If A is divisible by 21 then
\(\begin{array}{l}10^{a_{1}}+10^{a_{2}}+10^{a_{3}}+….\end{array} \)
must be divisible by 3.
For this we have
\(\begin{array}{l}^{6}C_0+^{6}C_3+^{6}C_6\end{array} \)
cases are there
\(\begin{array}{l}\therefore n(E)=^{6}C_0+^{6}C_3+^{6}C_6=22\end{array} \)
β΄ Required probability
\(\begin{array}{l}=\frac{22}{2^6}=p\end{array} \)
\(\begin{array}{l}\therefore \frac{11}{32}=p\end{array} \)
β΄ 96p = 33
JEE Main 2022 Paper Solutions – June 26th Shift 2
JEE Main 2022 June 26 Shift 2 Question Paper – Physics Solutions
JEE Main 2022 June 26 Shift 2 Question Paper – Chemistry Solutions
JEE Main 2022 June 26 Shift 2 Question Paper – Maths Solutions
Frequently Asked Questions β FAQs
Q1
What is the overall difficulty level of JEE Main June 26, 2022, Shift 2 Maths question paper?
The overall difficulty level of JEE Main 2022 June 26 Shift 2 Maths question paper is 1.86 out of 3.
Q2
How was the class-wise distribution of questions in the JEE Main 2022 June 26 Shift 2 Maths question paper?
There were 11 questions from Class 11 and 11 questions from Class 12 as per the memory-based questions in the JEE Main 2022 June 26 Shift 2 Maths question paper.
Q3
Was there any question from the Conic section in the JEE Main 2022 June 26 Shift 2 Maths question paper?
Yes. There was a question asked from the Conic section and it was an easy question.
Q4
How was the JEE Main 2022 June 26 Shift 2 Maths question paper?
The JEE Main 2022 June 26 Shift 2 Maths question paper was easy to moderate difficulty. There were 6 easy questions, 13 medium questions and 3 difficult questions as per the memory-based questions.
Q5
How many questions should the students attempt in the JEE Main 2022 June 26 Shift 2 Maths question paper?
There are total of 30 questions, of which 20 are from section A, and 10 are from section B. Students should attempt 25 questions in the JEE Main 2022 June 26 Shift 2 Maths question paper. They need to do only 5 out of 10 questions from section B.
Comments