The JEE Main 2022 June 29 – Shift 1 Maths Question Paper with Solutions are given on this page. These step-by-step solutions help students to learn how to solve problems using easy tricks. JEE aspirants can use the JEE Main 2022 answer keys to evaluate their performance in the JEE Main 2022 exams. All the solutions are prepared by our subject experts. Practising the JEE Main 2022 question paper with solutions helps students to develop adept problem-solving skills for any entrance exam. Students can easily access the JEE Main 2022 June 29 – Shift 1 Maths Question Paper with Solutions in PDF format from our webpage.
JEE Main 2022 June 29th Maths Shift 1 Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. The probability that a randomly chosen 2 × 2 matrix with all the entries from the set of first 10 primes, is singular, is equal to :
\(\begin{array}{l}(A)\ \frac{133}{10^4} \end{array} \)
\(\begin{array}{l}(B)\ \frac{18}{10^3} \end{array} \)
\(\begin{array}{l}(C)\ \frac{19}{10^3} \end{array} \)
\(\begin{array}{l}(D)\ \frac{271}{10^4} \end{array} \)
Answer (C)
Sol. Let A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
Let E be the event that matrix of order 2 × 2 is singular
Case-I
All entries are same example
\(\begin{array}{l}\begin{bmatrix}2 & 2 \\2 & 2 \\\end{bmatrix}\end{array} \)
= 10C1
Case-II
Matrix with two prime numbers only example
\(\begin{array}{l}\begin{bmatrix}3 & 5 \\3 & 5 \\\end{bmatrix}\end{array} \)
= 10C2 × 2! × 2!
\(\begin{array}{l}P\left ( E \right )=\frac{^{10}C_1+^{10}C_2\times2!\times2!}{10^4}=\frac{190}{10^4}=\frac{19}{10^3}\end{array} \)
2. Let the solution curve of the differential equation \(\begin{array}{l}x\frac{dy}{dx}-y=\sqrt{y^2+16x^2},\end{array} \)
y(1) = 3 be y = y(x). Then y(2) is equal to :
(A) 15
(B) 11
(C) 13
(D) 17
Answer (A)
Sol.
\(\begin{array}{l}x\frac{dy}{dx}-y=\sqrt{y^2+16x^2}\end{array} \)
y = 4x tan θ
\(\begin{array}{l}\frac{dy}{dx}=4\tan\theta+4x\sec^2\theta\frac{d\theta}{dx} \end{array} \)
\(\begin{array}{l}4x\tan\theta+4x^2\sec^2\theta\frac{d\theta}{dx}-4x\tan\theta=4x\sec\theta \end{array} \)
\(\begin{array}{l}\int\sec\theta~d\theta=\int\frac{dx}{x} \end{array} \)
log |secθ + tanθ| = log |x| + C
y(1) = 3 ⇒ 3 = 4 tanθ
\(\begin{array}{l}\tan\theta=\frac{3}{4}\Rightarrow \sec\theta=\frac{5}{4} \end{array} \)
\(\begin{array}{l}\ln\left|\frac{8}{4} \right|=\ln\left|1 \right|+C\end{array} \)
⇒ C = ln 2
∴ |secθ + tanθ| = 2|x|
To find y(2) put x = 2
\(\begin{array}{l}\Rightarrow \tan\theta=\frac{y}{8} \end{array} \)
(secθ + tanθ)2 = 16
\(\begin{array}{l}\sec\theta+\tan\theta=\pm4\\~~~~~\underline{\sec\theta-\tan\theta=\pm\frac{1}{4}}\\2\tan\theta=\frac{15}{4}=2\times\frac{y}{8} \end{array} \)
⇒ y = 15
3. If the mirror image of the point (2, 4, 7) in the plane 3x – y + 4z = 2 is (a, b, c), then 2a + b + 2c is equal to:
(A) 54
(B) 50
(C) –6
(D) –42
Answer (C)
Sol. Mirror image of (2, 4, 7) in 3x – y + 4z = 2 is
(a, b, c) then
\(\begin{array}{l}\frac{a-2}{3}=\frac{b-4}{-1}=\frac{c-7}{4}=\frac{-2\left ( 6-4+28-2 \right )}{3^2+\left ( -1 \right )^2+4^2} \end{array} \)
\(\begin{array}{l}\frac{a-2}{3}=\frac{b-4}{-1}=\frac{c-7}{4}=\frac{-28}{13}\end{array} \)
\(\begin{array}{l}a=\frac{-58}{13}~~b=\frac{80}{13}~~c=\frac{-21}{13} \end{array} \)
\(\begin{array}{l}2a+b+2c=\frac{-116+80-42}{13}\end{array} \)
= –6
4. Let ƒ : R ⇒ R be a function defined by :
\(\begin{array}{l}f\left ( x \right )=\left\{\begin{matrix}\underset{t\leq x}{\max}\left\{t^3-3t \right\} & :&x\leq 2 \\x^2+2x-6 &:&2<x<3 \\\left [x-3 \right ]+9 & :&3\leq x\leq 5 \\2x+1&:&x>5\end{matrix}\right. \end{array} \)
where [t] is the greatest integer less than or equal to t. Let m be the number of points where ƒ is not differentiable and \(\begin{array}{l}l=\displaystyle\int\limits_{-2}^2f\left ( x \right )dx\end{array} \)
Then the ordered pair (m, I) is equal to :
\(\begin{array}{l}(A)\ \left ( 3,\frac{27}{4} \right ) \end{array} \)
\(\begin{array}{l}(B)\ \left ( 3,\frac{23}{4} \right ) \end{array} \)
\(\begin{array}{l}(C)\ \left ( 4,\frac{27}{4} \right ) \end{array} \)
\(\begin{array}{l}(D)\ \left ( 4,\frac{23}{4} \right ) \end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\underset{t\leq x}{\max}\left\{t^3-3t \right\} ;x\leq2 \end{array} \)
g(t) = t3 –3t ⇒ g′(t) = 3t2 –3 = 3(t – 1)(t + 1)

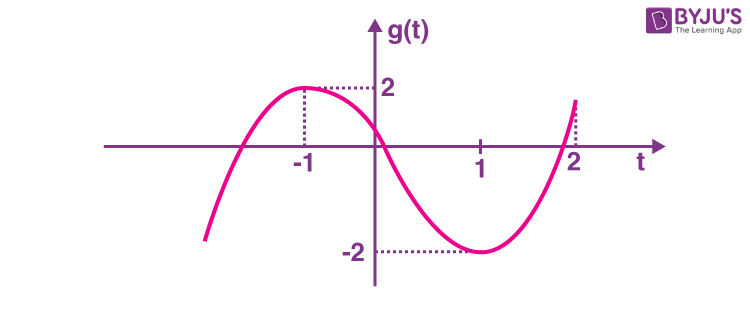
\(\begin{array}{l}f\left ( x \right )=\left\{\begin{matrix}x^3-3x & x<-1 \\ 2& -1\leq x\leq2 \\x^2+2x-6 & 2<x<3 \\9 & 3\leq x<4 \\10 & 4\leq x <5 \\11 & x=5 \\2x+1 & x>5 \\\end{matrix}\right. \end{array} \)
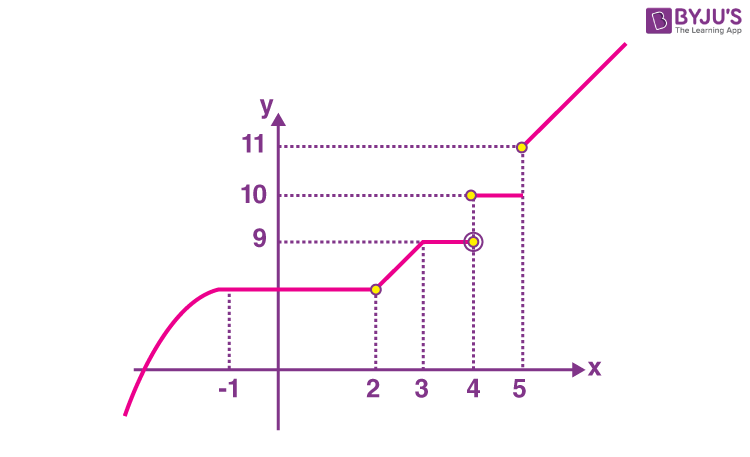
Points of non-differentiability = {2, 3, 4, 5}
⇒ m = 4
\(\begin{array}{l} l=\displaystyle\int\limits_{-2}^2f\left ( x \right )dx= \displaystyle\int\limits_{-2}^{-1}\left ( x^3-3x \right )dx+\displaystyle\int\limits_{-1}^{2}2dx\end{array} \)
\(\begin{array}{l}=\left [ \frac{x^4}{4}-\frac{3x^2}{2} \right ]_{-2}^{-1}+2\left ( 2+1 \right )=\left ( \frac{1}{4}-\frac{3}{2} \right )-\left ( 4-6 \right )+6\end{array} \)
\(\begin{array}{l}=\frac{27}{4} \end{array} \)
5. Let \(\begin{array}{l}\vec{a}=\alpha\hat{i}+3\hat{j}-\hat{k},\vec{b}=3\hat{i}-\beta\hat{j}+4\hat{k}\ \text{and}\ \vec{c}=\hat{i}+2\hat{j}-2\hat{k}\end{array} \)
where α, β ∈ R, be three vectors. If the projection of \(\begin{array}{l}\vec{a}\ \text{on}\ \vec{c}\ is\ \frac{10}{3}\ \text{and}\ \vec{b}\times\vec{c}=-6\hat{i}+10\hat{j}+7\hat{k}\end{array} \)
then the value of α + β is equal to :
(A) 3
(B) 4
(C) 5
(D) 6
Answer (A)
Sol.
\(\begin{array}{l}\vec{a}=\alpha\hat{j}+3\hat{j}-\hat{k}\end{array} \)
\(\begin{array}{l}\vec{b}=3\hat{i}-\beta\hat{j}+4\hat{k} \end{array} \)
\(\begin{array}{l}\vec{c}=\hat{i}+2\hat{j}-2\hat{k} \end{array} \)
\(\begin{array}{l}\text{Projection of}\ \vec{a}\ \text{on}\ \vec{c}\ is\end{array} \)
\(\begin{array}{l}\frac{\vec{a}\cdot\vec{c}}{\left|\vec{b} \right|}=\frac{10}{3}\end{array} \)
\(\begin{array}{l}\frac{\alpha+6+2}{\sqrt{1^2+2^2+\left ( -2 \right )^2}}=\frac{\alpha+8}{3}=\frac{10}{3}\end{array} \)
∴ α = 2
\(\begin{array}{l}\vec{b}\times\vec{c}=-6\hat{i}+10\hat{j}+7\hat{k} \end{array} \)
\(\begin{array}{l}\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\3 & -\beta & 4 \\1 & 2 & -2 \\\end{vmatrix}=\left ( 2\beta-8 \right )\hat{i}+10\hat{j}+\left ( 6+\beta \right )\hat{k}=-6\hat{i}+10\hat{j}+7\hat{k}\end{array} \)
\(\begin{array}{l}2\beta-8=-6~~\&~~6+\beta=7\end{array} \)
∴ β = 1
α + β = 2 + 1 = 3
6. The area enclosed by y2 = 8x and y = √2x that lies outside the triangle formed by \(\begin{array}{l}y=\sqrt{2}x,~x=1,~y=2\sqrt{2}\end{array} \)
is equal to :
\(\begin{array}{l}(A)\ \frac{16\sqrt{2}}{6}\end{array} \)
\(\begin{array}{l}(B)\ \frac{11\sqrt{2}}{6}\end{array} \)
\(\begin{array}{l}(C)\ \frac{13\sqrt{2}}{6}\end{array} \)
\(\begin{array}{l}(D)\ \frac{5\sqrt{2}}{6}\end{array} \)
Answer (C)
Sol.
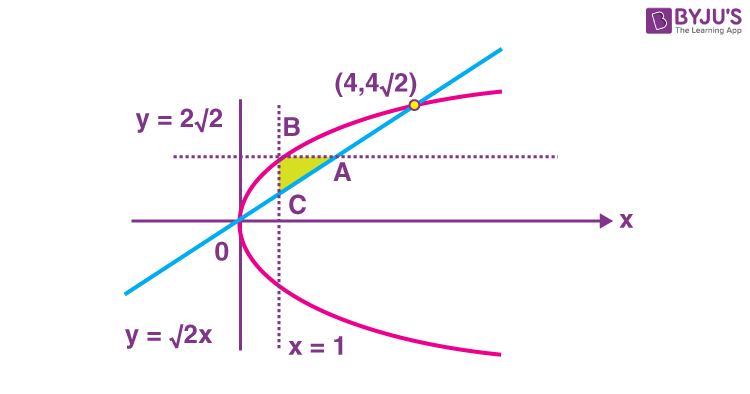
\(\begin{array}{l}A\left ( 2,2\sqrt{2} \right ),B\left ( 1,2\sqrt{2} \right ),C\left ( 1,\sqrt{2} \right )\end{array} \)
\(\begin{array}{l}\text{Area} = \displaystyle\int\limits_0^{4\sqrt{2}}\left ( \frac{y}{\sqrt{2}}-\frac{y^2}{8} \right )dy-\textup{area}~\left ( \Delta BAC \right )\end{array} \)
\(\begin{array}{l}=\left [\frac{y^2}{2\sqrt{2}}-\frac{y^3}{24} \right ]_0^{4\sqrt{2}}-\frac{1}{2}\times AB\times BC\end{array} \)
\(\begin{array}{l}=8\sqrt{2}-\frac{32\times 4\sqrt{2}}{24}-\frac{1}{2}\times1\times\sqrt{2}\end{array} \)
\(\begin{array}{l}=8\sqrt{2}-\frac{16\sqrt{2}}{3}-\frac{\sqrt{2}}{2} \end{array} \)
\(\begin{array}{l}=\frac{\sqrt{2}}{6}\left ( 48-32-3 \right )=\frac{13\sqrt{2}}{6} \end{array} \)
7. If the system of linear equations
2x + y – z = 7
x – 3y + 2z = 1
x + 4y + δz = k, where δ, k ∈ R
has infinitely many solutions, then δ + k is equal to:
(A) –3
(B) 3
(C) 6
(D) 9
Answer (B)
Sol. 2x + y – z = 7
x – 3y + 2z = 1
x + 4y + δz = k
\(\begin{array}{l}\Delta=\begin{vmatrix}2 & 1 & -1\\1 & -3 & 2 \\1 & 4 & \delta \\\end{vmatrix} =-7\delta-21=0\end{array} \)
\(\begin{array}{l}\delta=-3\end{array} \)
\(\begin{array}{l}\Delta_1=\begin{vmatrix}7 & 1 & -1\\1 & -3 & 2 \\k & 4 & -3 \\\end{vmatrix}\end{array} \)
⇒ 6 – k = 0 ⇒k = 6
δ + k = -3 + 6 = 3
8. Let α and β be the roots of the equation x2 + (2i – 1) = 0. Then, the value of |α2 + β2| is equal to:
(A) 50
(B) 250
(C) 1250
(D) 1500
Answer (A)
Sol. x2 + 2i – 1 = 0
α2 = β2 = 1 – 2i
α4 = (1 – 2i)2 = 1 + (2i)2 – 4i = –3 – 4i
α8 = (–3 – 4i)2 = 9 – 16 + 24i = –7 + 24i
\(\begin{array}{l}\left|\alpha^8+\beta^8 \right|=2\left|-7+24i \right|=2\sqrt{\left ( -7 \right )^2+\left ( 24 \right )^2}=50\end{array} \)
9. Let \(\begin{array}{l}\Delta\in \left\{\wedge,\vee,\Rightarrow,\Leftrightarrow \right\}\ \text{be such that}\left( p\wedge q \right)\Delta \left( \left( p\vee q \right)\Rightarrow q \right)\end{array} \)
is a tautology. Then Δ is equal to :
\(\begin{array}{l}(A)\ \wedge \end{array} \)
\(\begin{array}{l}(B)\ \vee\end{array} \)
\(\begin{array}{l}(C)\ \Rightarrow\end{array} \)
\(\begin{array}{l}(D)\ \Leftrightarrow\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\left ( p\vee q \right )\Rightarrow q \end{array} \)
\(\begin{array}{l}\sim \left ( p\vee q \right )\vee q \end{array} \)
\(\begin{array}{l}= \left (\sim p\wedge \sim q \right )\vee q \end{array} \)
\(\begin{array}{l}=\left ( \sim p\vee q \right )\wedge\left ( \sim q\vee q \right )\end{array} \)
\(\begin{array}{l}=\left ( \sim p\vee q \right )\wedge T\end{array} \)
\(\begin{array}{l}=\sim p\vee q\end{array} \)
Now
\(\begin{array}{l}\left ( p\wedge q \right )\Delta \left ( \sim p \vee q \right ) \end{array} \)
\(\begin{array}{l}\begin{matrix}p & q & \sim p & p\wedge q & \sim p\vee q & \left ( p\wedge q \right )\Delta\left ( \sim p\vee q \right ) \\T & T & F & T & T & T \\T & F & F & F & F & T \\F & T & T & F & T & T \\F & F & T & F & T & T \\\end{matrix}\end{array} \)
∴ Δ = ⇒
10. Let A = [aij] be a square matrix of order 3 such that aij = 2j–i, for all i, j = 1, 2, 3. Then, the matrix A2 + A3 + … + A10 is equal to :
\(\begin{array}{l}(A)\ \left ( \frac{3^{10}-3}{2} \right )A\end{array} \)
\(\begin{array}{l}(B)\ \left ( \frac{3^{10}-1}{2} \right )A\end{array} \)
\(\begin{array}{l}(C)\ \left ( \frac{3^{10}+1}{2} \right )A\end{array} \)
\(\begin{array}{l}(D)\ \left ( \frac{3^{10}+3}{2} \right )A\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}A=\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \\\end{bmatrix}=\begin{bmatrix}2^0 & 2^1 & 2^2 \\2^{-1} & 2^0 & 2^1 \\2^{-2} & 2^{-1} & 2^0 \\\end{bmatrix}\end{array} \)
\(\begin{array}{l}A^2=\begin{bmatrix}1 & 2 & 4 \\\frac{1}{2} & 1 & 2 \\\frac{1}{4} & \frac{1}{2} & 1 \\\end{bmatrix}\begin{bmatrix}1 & 2 & 4 \\\frac{1}{2} & 1 & 2 \\\frac{1}{4} & \frac{1}{2} & 1 \\\end{bmatrix} =\begin{bmatrix}3 & 6 & 12 \\\frac{3}{2} & 3 & 6 \\\frac{3}{4} & \frac{3}{2} & 3 \\\end{bmatrix}=3A\end{array} \)
A2 = 3A
A3 = A.A2 = A(3A) = 3A2 = 32A
A4 = 33A
Now
A2 + A3 + … + A10
A[31 + 32 + 33 + … + 39]
\(\begin{array}{l}=\frac{3\left [ 3^9-1 \right ]}{3-1}A\end{array} \)
\(\begin{array}{l}=\frac{\left ( 3^{10}-3 \right )}{2}A\end{array} \)
11. Let a set A = A1 ⋃ A2 ⋃ …⋃ Ak, where Ai ⋂ Aj = Φ for i ≠ j, 1 ≤ i, j ≤ k. Define the relation R from A to A by R = {(x, y) : y ∈ Ai if and only if x ∈ Ai, 1 ≤ i ≤ k}. Then, R is :
(A) reflexive, symmetric but not transitive
(B) reflexive, transitive but not symmetric
(C) reflexive but not symmetric and transitive
(D) an equivalence relation
Answer (D)
Sol. R = {(x, y) :y ∈ Ai, iff x ∈ Ai, 1 ≤ i ≤ k}
(1) Reflexive
(a, a) ⇒ a ∈ Ai iff a ∈ Ai
(2) Symmetric
(a, b) ⇒a ∈Ai iff b ∈ Ai
(b, a) ∈ R as b ∈ Ai iff a ∈ Ai
(3) Transitive
(a, b) ∈ R & (b, c) ∈ R.
⇒ a ∈ Ai iff b ∈ Ai & b ∈ Ai iff c ∈ Ai
⇒ a ∈ Ai iff c ∈ Ai
⇒ (a, c) ∈ R.
⇒ Relation is equivalence
12. Let \(\begin{array}{l}\left\{a_n \right\}_{n=0}^\infty\end{array} \)
be a sequence such that a0 = a1 = 0 and an + 2 = 2an + 1 – an + 1 for all n ≥ 0. \(\begin{array}{l}\text{Then}\ \displaystyle\sum\limits_{n=2}^\infty\frac{a_n}{7^n}\ \text{is equal to}:\end{array} \)
\(\begin{array}{l}(A)\ \frac{6}{343}\end{array} \)
\(\begin{array}{l}(B)\ \frac{7}{216}\end{array} \)
\(\begin{array}{l}(C)\ \frac{8}{343}\end{array} \)
\(\begin{array}{l}(D)\ \frac{49}{216}\end{array} \)
Answer (B)
Sol.
an+2 = 2an+1 – an + 1 & a0 = a1 = 0
a2 = 2a1 – a0 + 1 = 1
a3 = 2a2 – a1 + 1 = 3
a4 = 2a3 – a2 + 1 = 6
a5 = 2a4 – a3 + 1 = 10
\(\begin{array}{l}\displaystyle\sum\limits_{n=2}^\infty\frac{a_n}{7^n}=\frac{a_2}{7^2}+\frac{a_3}{7^3}+\frac{a_4}{7^4}+\dots\end{array} \)
\(\begin{array}{l}s=\frac{1}{7^2}+\frac{3}{7^3}+\frac{6}{7^4}+\frac{10}{7^5}+\dots\\~~~~~\underline{\frac{1}{7}s=\frac{1}{7^3}+\frac{3}{7^4}+\frac{6}{7^5}+\dots}\\~~~~~\frac{6s}{7}=\frac{1}{7^2}+\frac{2}{7^3}+\frac{3}{7^4}+\dots\\~~~~~\underline{\frac{6s}{49}=~~~~~~\frac{1}{7^3}+\frac{2}{7^4}+\dots}\\~~~~~\frac{36s}{49}=\frac{1}{7^2}+\frac{1}{7^3}+\frac{1}{7^4}+\dots \end{array} \)
\(\begin{array}{l}\frac{36s}{49}=\frac{7^\frac{1}{2}}{1-\frac{1}{7}}\end{array} \)
\(\begin{array}{l}\frac{36s}{49}=\frac{7}{49\times6} \end{array} \)
\(\begin{array}{l}s=\frac{7}{216} \end{array} \)
13. The distance between the two points A and A′ which lie on y = 2 such that both the line segments AB and A′B (where B is the point (2, 3)) subtend angle π/4 at the origin, is equal to
(A) 10
(B) 48/5
(C) 52/5
(D) 3
Answer (C)
Sol. Let A(α, 2) Given B(2, 3)
\(\begin{array}{l}m_{OA}=\frac{2}{\alpha}~~\&~~m_{OB}=\frac{3}{2} \end{array} \)
\(\begin{array}{l}\tan\frac{\pi}{4}=\left|\frac{\frac{2}{\alpha}-\frac{3}{2}}{1+\frac{2}{\alpha}\cdot\frac{3}{2}} \right|\Rightarrow\frac{4-3\alpha}{2\alpha+6}=\pm1\end{array} \)
4 – 3α = 2α + 6 & 4 – 3α = -2α – 6
\(\begin{array}{l}\alpha=\frac{-2}{5}~~\&~~\alpha=10\end{array} \)
\(\begin{array}{l}A\left ( -\frac{2}{5},2 \right )~\&~A’\left ( 10,2 \right )~\textup{and}~B\left ( 2,3 \right )\end{array} \)
\(\begin{array}{l}AA’=10+\frac{2}{5}=\frac{52}{5}\end{array} \)
14. A wire of length 22 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into an equilateral triangle. Then, the length of the side of the equilateral triangle, so that the combined area of the square and the equilateral triangle is minimum, is
\(\begin{array}{l}(A)\ \frac{22}{9+4\sqrt{3}}\end{array} \)
\(\begin{array}{l}(B)\ \frac{66}{9+4\sqrt{3}}\end{array} \)
\(\begin{array}{l}(C)\ \frac{22}{4+9\sqrt{3}}\end{array} \)
\(\begin{array}{l}(D)\ \frac{66}{4+9\sqrt{3}}\end{array} \)
Answer (B)
Sol.
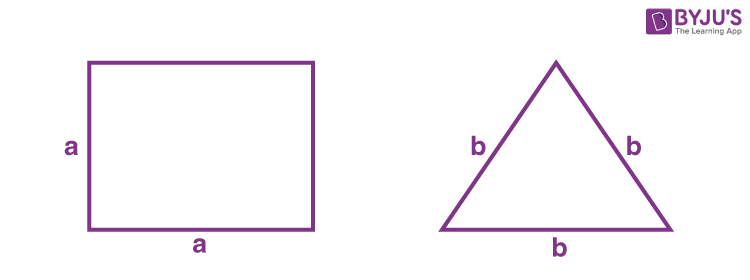
4a + 3b = 22
Total area = A
\(\begin{array}{l}=a^2+\frac{\sqrt{3}}{4}b^2 \end{array} \)
\(\begin{array}{l}A=\left ( \frac{22-3b}{4} \right )^2+\frac{\sqrt{3}}{4}b^2\end{array} \)
\(\begin{array}{l}\frac{dA}{dB}=2\left ( \frac{22-3b}{4} \right )\left ( \frac{-3}{4} \right )+\frac{\sqrt{3}}{4}\cdot2b=0 \end{array} \)
\(\begin{array}{l}\Rightarrow \frac{\sqrt{3b}}{2}=\frac{3}{8}\left ( 22-3b \right )\end{array} \)
\(\begin{array}{l}4\sqrt{3}b=66-9b \end{array} \)
\(\begin{array}{l}b=\frac{66}{9+4\sqrt{3}} \end{array} \)
15. The domain of the function \(\begin{array}{l}\cos^{-1}\left ( \frac{2\sin^{-1}\left ( \frac{1}{4x^2-1} \right )}{\pi} \right )\end{array} \)
is :
\(\begin{array}{l}(A)\ \textbf{R}-\left\{-\frac{1}{2},\frac{1}{2} \right\}\end{array} \)
\(\begin{array}{l}(B)\ \left (-\infty,-1 \left . \right ]\cup\left [1,\infty \right . \right )\cup\left\{ 0\right\}\end{array} \)
\(\begin{array}{l}(C)\ \left ( -\infty,\frac{-1}{2} \right )\cup\left ( \frac{1}{2},\infty \right ) \cup\left\{0 \right\}\end{array} \)
\(\begin{array}{l}(D)\ \left (-\infty,\frac{-1}{\sqrt{2}} \right ]\cup\left [ \frac{1}{\sqrt{2}},\infty \right )\cup\left\{0 \right\}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}-1\leq\frac{2}{\pi}\sin^{-1}\left ( \frac{1}{4x^2-1} \right ) \leq 1\end{array} \)
\(\begin{array}{l}-\frac{\pi}{2}\leq\sin^{-1}\frac{1}{4x^2-1}\leq\frac{\pi}{2}\end{array} \)
\(\begin{array}{l}-1\leq\frac{1}{4x^2-1}\leq 1\end{array} \)
\(\begin{array}{l}\frac{1}{4x^2-1}\geq-1\Rightarrow\frac{4x^2}{\left ( 2n+1 \right )\left ( 2x-1 \right )}\geq0\end{array} \)
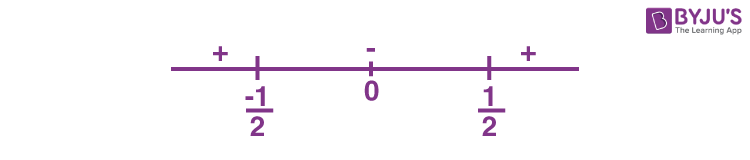
\(\begin{array}{l}x\in\left (-\infty,\frac{-1}{2} \right )\cup\left ( 0 \right ) \cup\left ( \frac{1}{2},\infty \right )….(1)\end{array} \)
\(\begin{array}{l}\frac{1}{4x^2-1}\leq1\Rightarrow1-\frac{1}{4x^2-1}\geq 0\Rightarrow\frac{4x^2-2}{4x^2-1}\geq0\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{\left ( x+\frac{1}{\sqrt{2}} \right )\left ( x-\frac{1}{\sqrt{2}}\right )}{\left ( x+\frac{1}{2} \right )\left ( x-\frac{1}{2} \right )}\geq 0\end{array} \)
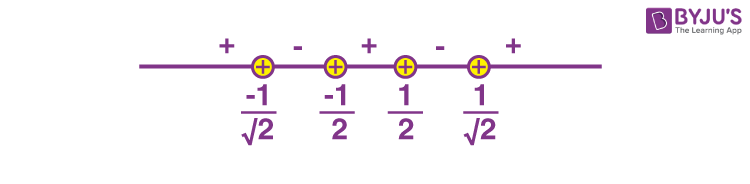
\(\begin{array}{l}x\in\left ( -\infty,\frac{-1}{\sqrt{2}} \right ]\cup\left ( \frac{-1}{2},\frac{1}{2} \right ) \cup\left ( \frac{1}{\sqrt{2}},\infty \right )\dots\left ( 2 \right )….(2)\end{array} \)
From (1) & (2)
\(\begin{array}{l}x\in\left ( -\infty,\frac{-1}{\sqrt{2}} \right]\cup\left [ \frac{1}{\sqrt{2}},\infty \right )\cup\left\{0 \right\}\end{array} \)
16. If the constant term in the expansion of \(\begin{array}{l}\left ( 3x^3-2x^2+\frac{5}{x^5} \right ) ^{10}\end{array} \)
is 2k·l, where l is an odd integer, then the value of k is equal to
(A) 6
(B) 7
(C) 8
(D) 9
Answer (D)
Sol. Constant term in
\(\begin{array}{l}\left ( 3x^3-2x^2+\frac{5}{x^5} \right )^{10}\rightarrow x^0\end{array} \)
⇒ (3x8 – 2x7 + 5)10→x50
General term of (3x8 – 2x7 + 5)10 is
\(\begin{array}{l}\frac{10!}{p!q!r!}\left ( 3x^8 \right )^p\left ( -2x^7 \right )^q\left ( 5 \right )^r\end{array} \)
Here 8p + 7q = 50 and p + q+r = 10
⇒ p = 1, q = 6, r = 3 is only valid solution
\(\begin{array}{l}\therefore \frac{10!}{1!6!r!}3^1~2^6\cdot5^3=2^k\cdot l\end{array} \)
\(\begin{array}{l}\Rightarrow 5\cdot3\cdot7\cdot5^3\cdot3\cdot2^9=2^kl \end{array} \)
∴ k = 9
17. \(\begin{array}{l}\displaystyle\int\limits_0^5\cos\left ( \pi\left ( x-\left [ \frac{x}{2} \right ] \right ) \right )dx\end{array} \)
, where [t] denotes greatest integer less than or equal to t, is equal to
(A) –3
(B) –2
(C) 2
(D) 0
Answer (D)
Sol.
\(\begin{array}{l}\displaystyle\int\limits_0^5\cos\left(\begin{matrix}\pi\left(x-\left[\frac{x}{2}\right]\right )\end{matrix}\right.dx\end{array} \)
\(\begin{array}{l}=\displaystyle\int\limits_0^2\cos\left ( \pi x\right )dx+\displaystyle\int\limits_2^4\cos\left ( \pi\left ( x-1 \right ) \right )dx+\displaystyle\int\limits_4^5\cos\left ( \pi\left ( x-2 \right ) \right )dx\end{array} \)
\(\begin{array}{l}\left.\begin{matrix}\frac{\sin\pi x}{\pi}\end{matrix}\right|_0^2\left.\begin{matrix}+\frac{\sin\left ( \pi\left ( x-1 \right ) \right )}{\pi}\end{matrix}\right|_2^4+\left.\begin{matrix}\frac{\sin\left ( \pi\left ( x-2 \right ) \right )}{\pi}\end{matrix}\right|_4^5\end{array} \)
= 0 + 0 + 0 = 0
18. Let PQ be a focal chord of the parabola y2 = 4x such that it subtends an angle of π/2 at the point (3, 0). Let the line segment PQ be also a focal chord of the ellipse \(\begin{array}{l}E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,a^2>b^2\end{array} \)
. If e is the eccentricity of the ellipse E, then the value of 1/e2 is equal to
(A) 1 + √2
(B) 3 + 2√2
(C) 1 + 2√3
(D) 4 + 5√3
Answer (B)
Sol.
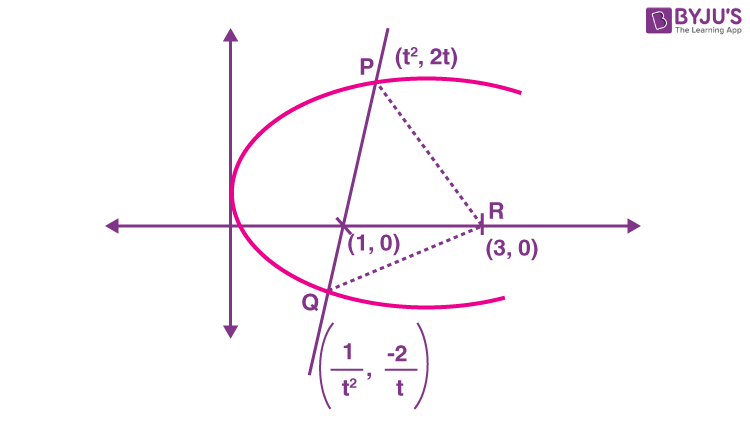
As
\(\begin{array}{l}\angle PRQ=\frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\left ( \frac{\frac{2}{t}}{3-\frac{1}{t^2}} \right ) \cdot\left ( \frac{-2t}{3-t^2} \right )=-1\end{array} \)
⇒ t = ± 1
∴ P ≡ (1, 2) & Q(1, –2)
∴ for ellipse
\(\begin{array}{l}\frac{1}{a^2}+\frac{4}{b^2}=1\end{array} \)
and ae = 1
\(\begin{array}{l}\Rightarrow \frac{1}{a^2}+\frac{4}{a^2\left ( 1-e^2 \right )}=1\end{array} \)
\(\begin{array}{l}\Rightarrow 1+\frac{4}{\left ( 1-e^2 \right )} =\frac{1}{e^2}\end{array} \)
⇒ (5 – e2)e2 = 1 – e2
⇒ e4 – 6e2 + 1 = 0
\(\begin{array}{l}\Rightarrow e^2=\frac{1}{3-2\sqrt{2}}\Rightarrow \frac{1}{e^2}=3+2\sqrt{2}\end{array} \)
19. Let the tangent to the circle C1: x2 + y2 = 2 at the point M(–1, 1) intersect the circle C2: (x – 3)2 + (y – 2)2 = 5, at two distinct points A and B. If the tangents to C2 at the points A and B intersect at N, then the area of the triangle ANB is equal to
\(\begin{array}{l}(A)\ \frac{1}{2} \end{array} \)
\(\begin{array}{l}(B)\ \frac{2}{3} \end{array} \)
\(\begin{array}{l}(C)\ \frac{1}{6} \end{array} \)
\(\begin{array}{l}(D)\ \frac{5}{3} \end{array} \)
Answer (C)
Sol. Tangent toC1 at M: –x + y = 2 ≡T
Intersection of T with C2⇒ (x – 3)2 + x2 = 5
⇒ x = 1, 2
A(1, 3) and B(2, 4)
Let N ≡ (α, β)
Then –x + y = 2 shall be chord of contact for x2 + y2 – 6x – 4y + 8 = 0
\(\begin{array}{l}\therefore \alpha x+\beta y-3x-3\alpha-2y-2\beta+8=0 \end{array} \)
is same as –x + y = 2
\(\begin{array}{l}\frac{\alpha-3}{-1}=\frac{\beta-2}{1}=\frac{3\alpha-8+2\beta}{2} \end{array} \)
\(\begin{array}{l}\Rightarrow \left ( \alpha,\beta \right )\equiv\left ( \frac{4}{3},\frac{11}{3} \right ) \end{array} \)
\(\begin{array}{l}\Delta=\frac{1}{2}\begin{vmatrix}1 & 3 & 1 \\2 & 4 & 1 \\4/3 & 11/3 & 1 \\\end{vmatrix}=\frac{1}{6}\ \text{units}\end{array} \)
20. Let the mean and the variance of 5 observations x1, x2, x3, x4, x5 be 24/5 and 194/25, respectively. If the mean and variance of the first 4 observations are 7/2 and a, respectively, then (4a + x5) is equal to
(A) 13
(B) 15
(C) 17
(D) 18
Answer (B)
Sol.
\(\begin{array}{l}\displaystyle\sum\limits_{i=1}^5x_i=24 ….(i)\end{array} \)
\(\begin{array}{l}\frac{\displaystyle\sum\limits_{i=1}^5x_i^2 }{5} -\left ( \frac{24}{5} \right )^2=\frac{194}{25}\end{array} \)
\(\begin{array}{l}\Rightarrow \sum x_i^2=1154….(ii)\end{array} \)
\(\begin{array}{l}\displaystyle\sum\limits_{i=1}^4x_i=14\end{array} \)
⇒ x5 = 10
\(\begin{array}{l}a=\frac{\displaystyle\sum\limits_{i=1}^4x_i^2}{4}-\frac{49}{4}=\frac{54-49}{4}=\frac{5}{4}\end{array} \)
⇒ x5 + 4a = 10 + 5 = 15
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let \(\begin{array}{l} S=\{z\in C : \left| z-2\right| \le 1 \text { and }z(1+i) + \overline{z}(1-i)\le 2\}\end{array} \)
. Let |z – 4i| attains minimum and maximum values, respectively, at z1∈ S and z2∈ S. If \(\begin{array}{l}5\left ( \left|z_1 \right|^2+\left|z_2 \right|^2 \right )=\alpha+\beta\sqrt{5}\end{array} \)
where α and β are integers, then the value of α + β is equal to _____.
Answer (26)
Sol.
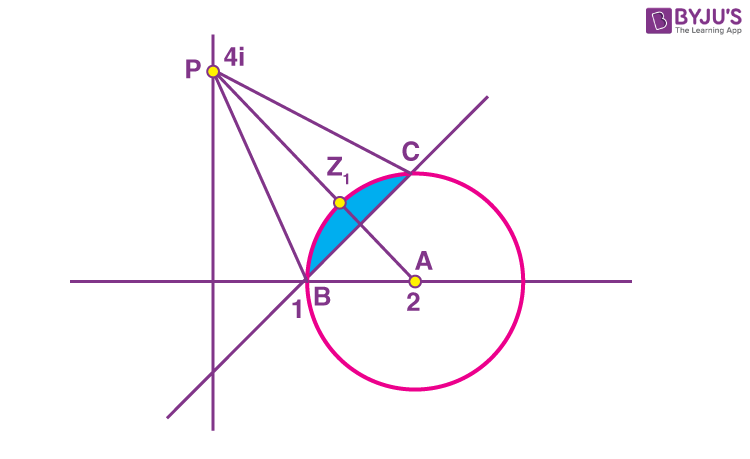
S represents the shaded region shown in the diagram.
Clearly, z1 will be the point of intersection of PA and given circle.
PA : 2x + y = 4 and given circle has equation
(x – 2)2 + y2 = 1.
On solving, we get
\(\begin{array}{l}z_1=\left ( 2-\frac{1}{\sqrt{5}} \right)+\frac{2}{5}i\Rightarrow \left|z_1 \right|^2=5-\frac{4}{\sqrt{5}}\end{array} \)
z2 will be either B or C.
\(\begin{array}{l}\because PB=\sqrt{17}~\textup{and}~PC=\sqrt{13}~\textup{hence}~z_2=1\end{array} \)
So
\(\begin{array}{l}5\left ( \left|z_1 \right|^2+\left|z_2 \right|^2 \right )=30-4\sqrt{5}\end{array} \)
Clearly α = 30 and β = –4 ⇒α + β = 26
2. Let y = y(x) be the solution of the differential equation \(\begin{array}{l}\frac{dy}{dx}+\frac{\sqrt{2}y}{2\cos^4x-\cos2x}=xe^{\tan^{-1}\left ( \sqrt{2}\cot2x \right )},0<x<\frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\text{with}\ y\left ( \frac{\pi}{4} \right )=\frac{\pi^2}{32}.\ \text{If}\ y\left ( \frac{\pi}{3} \right )=\frac{\pi^2}{18}e^{-\tan^{-1}\left ( \alpha \right )}\end{array} \)
then the value of 3α2 is equal to ______.
Answer (2)
Sol.
\(\begin{array}{l}\frac{dy}{dx}+\frac{2\sqrt{2}y}{1+\cos^2~2x}=xe^{\tan^{-1}\left ( \sqrt{2}\cot2x \right )}\end{array} \)
\(\begin{array}{l}I.F.=e^{\int\frac{2\sqrt{2}dx}{1+\cos^22x}}=e^{\sqrt{2}\int\frac{2\sec^22x}{2+\tan^22x}dx}\end{array} \)
\(\begin{array}{l}=e^{\tan^{-1}\left ( \frac{\tan2x}{\sqrt{2}} \right )}\end{array} \)
\(\begin{array}{l}\Rightarrow y.e^{\tan^{-1}\left ( \frac{\tan2x}{\sqrt{2}} \right )}=\int xe^{\tan^{-1}\left ( \sqrt{2}\cot2x \right )}.e^{\tan^{-1}\left ( \frac{\tan2x}{\sqrt{2}} \right )} dx+c\end{array} \)
\(\begin{array}{l}\Rightarrow y.e^{\tan^{-1}\left ( \frac{\tan2x}{\sqrt{2}} \right )} =e^{\frac{\pi}{2}}\cdot\frac{x^2}{2}+c\end{array} \)
When
\(\begin{array}{l}x=\frac{\pi}{4},y=\frac{\pi^2}{32}~\textup{gives}~c=0 \end{array} \)
When
\(\begin{array}{l}x=\frac{\pi}{3},y=\frac{\pi^2}{18}e^{-\tan^{-1}\alpha}\end{array} \)
So
\(\begin{array}{l}\frac{\pi^2}{18}e^{-\tan^{-1}\alpha}\cdot e^{-\tan^{-1}\left ( -\sqrt{\frac{3}{2}} \right )}=e^{\pi/2}\frac{\pi^2}{18}\end{array} \)
\(\begin{array}{l}\Rightarrow -\tan^{-1}\alpha+\tan^{-1}\left ( \sqrt{\frac{3}{2}} \right ) =\frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow \tan^{-1}\left ( -\alpha \right )=tan^{-1}\left ( \sqrt{\frac{2}{3}} \right ) \end{array} \)
\(\begin{array}{l}\Rightarrow \alpha=-\sqrt{\frac{2}{3}}\Rightarrow 3\alpha^2=2\end{array} \)
3. Let d be the distance between the foot of perpendiculars of the point P(1, 2, –1) and Q(2, –1, 3) on the plane –x + y + z = 1. Then d2 is equal to ____.
Answer (26)
Sol. Foot of perpendicular from P
\(\begin{array}{l}\frac{x-1}{-1}=\frac{y-2}{1}=\frac{z+1}{1}=\frac{-\left ( -1+2-1-1 \right )}{3}\end{array} \)
\(\begin{array}{l}\Rightarrow p’\equiv\left ( \frac{2}{3},\frac{7}{3},\frac{-2}{3} \right ) \end{array} \)
and foot of perpendicular from Q
\(\begin{array}{l}\frac{x-2}{-1}=\frac{y+1}{1}=\frac{z-3}{1}=\frac{-\left ( -2-1+3-1 \right )}{3}\end{array} \)
\(\begin{array}{l}\Rightarrow Q’\equiv\left ( \frac{5}{3},\frac{-2}{3},\frac{10}{3} \right ) \end{array} \)
\(\begin{array}{l}P’Q’=\sqrt{\left ( 1 \right )^2+\left ( 3 \right )^2+\left ( 4 \right )^2}=d=\sqrt{26} \end{array} \)
⇒ d2 = 26
4. The number of elements in the set \(\begin{array}{l}S=\left\{\theta\in\left [ -4\pi,4\pi \right ]:3\cos^2 2\theta+6\cos2\theta-10\cos^2\theta+5=0 \right\}\end{array} \)
is __________.
Answer (32)
Sol.
\(\begin{array}{l}3\cos^22\theta+6\cos2\theta-\frac{10\left ( 1+\cos2\theta \right )}{2}+5=0 \end{array} \)
⇒ 3cos22θ + cos2θ = 0
⇒ cos2θ = 0 or cos2θ = -1/3
As θ ∈[0, π], cos2θ = -⅓ ⇒ 2 times
⇒ θ ∈[–4π, 4π], cos2θ = -1/3 ⇒ 16 times
Similarly, cos2θ = 0 ⇒ 16 times
∴ Total 32 solutions
5. The number of solutions of the equation \(\begin{array}{l}2\theta-\cos^2\theta+\sqrt{2}=0 \end{array} \)
in R is equal to ___________.
Answer (1)
Sol.
\(\begin{array}{l}\cos^2\theta=2\theta+\sqrt{2}\end{array} \)
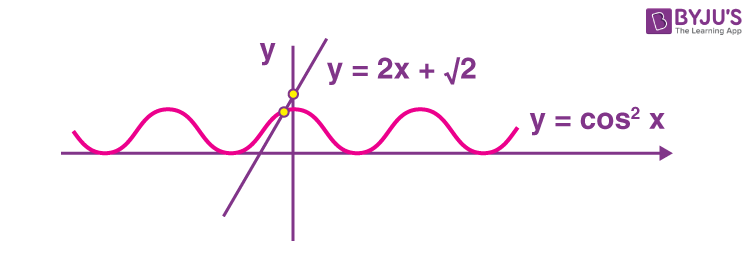
1 point of intersection = 1 solution.
6. \(\begin{array}{l}50\tan\left ( 3\tan^{-1}\left ( \frac{1}{2} \right )+2\cos^{-1}\left ( \frac{1}{\sqrt{5}} \right ) \right )+4\sqrt{2}\tan\left ( \frac{1}{2}\tan^{-1}\left ( 2\sqrt{2} \right ) \right )\end{array} \)
is equal to _____________.
Answer (29)
Sol.
\(\begin{array}{l}50\tan\left ( \tan^{-1}\frac{1}{2}+2\tan^{-1}\left (\frac{1}{2} \right )+2\tan^{-1}\left ( 2 \right ) \right )+4\sqrt{2}\tan\left ( \frac{\tan^{-1}}{2}\left ( 2\sqrt{2} \right ) \right )\end{array} \)
\(\begin{array}{l}\Rightarrow 50\tan\left ( \pi+\tan^{-1}\left ( \frac{1}{2} \right ) \right ) +4\sqrt{2}\tan\left ( \frac{1}{2}\tan^{-1}2\sqrt{2} \right )\end{array} \)
\(\begin{array}{l}\Rightarrow 50\left ( \frac{1}{2} \right )+4\sqrt{2}\tan\alpha\end{array} \)
Where
\(\begin{array}{l}2\alpha=\tan^{-1}2\sqrt{2} \end{array} \)
\(\begin{array}{l}\Rightarrow \frac{2\tan\alpha}{1-\tan^2\alpha} =2\sqrt{2}….(i)\end{array} \)
\(\begin{array}{l}\Rightarrow 2\sqrt{2}\tan^2\alpha+2\tan\alpha-2\sqrt{2} =0\end{array} \)
\(\begin{array}{l}\Rightarrow 2\sqrt{2}\tan^2\alpha+4\tan\alpha-2\tan\alpha-2\sqrt{2} =0\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( 2\sqrt{2}\tan\alpha-2 \right ) \left ( \tan\alpha-\sqrt{2} \right )=0\end{array} \)
\(\begin{array}{l}\Rightarrow \tan\alpha=\sqrt{2}~\textup{or}~\frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow \tan\alpha=\frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( \tan\alpha=\sqrt{2}~\textup{does not satisfy}\left ( i \right ) \right ) \end{array} \)
\(\begin{array}{l}\Rightarrow 25+4\sqrt{2}\frac{1}{\sqrt{2}}=29 \end{array} \)
7. Let c, k∈ R. If f(x) = (c + 1)x2 + (1 – c2)x + 2k and f(x + y) = f(x) + f(y) – xy, for all x, y ∈ R, then the value of \(\begin{array}{l}\left|2\left ( f\left ( 1 \right )+f\left ( 2 \right )+f\left ( 3 \right )+\dots+f\left ( 20 \right ) \right ) \right|\end{array} \)
is equal to ____________.
Answer (3395)
Sol. f(x) is polynomial
Put y = 1/x in given functional equation we get
\(\begin{array}{l}f\left ( x+\frac{1}{x} \right )=f\left ( x \right )+f\left ( \frac{1}{x} \right )-1\end{array} \)
\(\begin{array}{l}\Rightarrow \left ( c+1 \right )\left ( x+\frac{1}{x} \right )^2+\left ( 1-c^2 \right )\left ( x+\frac{1}{x} \right )+2K\end{array} \)
\(\begin{array}{l}=\left ( c+1 \right )x^2+\left ( 1-c^2 \right )x+2K+\left ( c+1 \right )\frac{1}{x^2}+\left ( 1-c^2 \right )\frac{1}{x}+2K-1\end{array} \)
⇒ 2(c + 1) = 2K – 1 …(1)
and put x = y = 0 we get
\(\begin{array}{l}f\left ( 0 \right )=2+f\left ( 0 \right )-0\Rightarrow f\left ( 0 \right )=0\Rightarrow k =0\end{array} \)
∴ k = 0 and 2c = –3 ⇒c = –3/2
\(\begin{array}{l}f(x) = -\frac{x^2}{2}-\frac{5x}{4}=\frac{1}{4}\left ( 5x+2x^2 \right )\end{array} \)
\(\begin{array}{l}\left|2\displaystyle\sum\limits_{i=1}^{20}f\left ( i \right ) \right| =\left|\frac{-2}{4}\left ( \frac{5.20.21}{2}+\frac{2.20.21.41}{6} \right ) \right|\end{array} \)
\(\begin{array}{l}=\left|\frac{-1}{2}\left ( 2730+5740 \right ) \right| \end{array} \)
\(\begin{array}{l}=\left|-\frac{6790}{2} \right| =3395\end{array} \)
.
8. Let H: \(\begin{array}{l}\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,a>0,b>0,\end{array} \)
be a hyperbola such that the sum of lengths of the transverse and the conjugate axes is\(\begin{array}{l}4\left ( 2\sqrt{2}+\sqrt{14} \right ).\ \text{If the eccentricity H is}\ \frac{\sqrt{11}}{2}, \end{array} \)
then the value of a2 + b2 is equal to ____________.
Answer (88)
Sol.
\(\begin{array}{l}2a+2b=4\left ( 2\sqrt{2}+\sqrt{14} \right )….(1) \end{array} \)
\(\begin{array}{l}1+\frac{b^2}{a^2}=\frac{11}{4}~~~~\dots\left ( 2 \right )\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{b^2}{a^2}=\frac{7}{4}~~~\dots\left ( 3 \right ) \end{array} \)
and
\(\begin{array}{l}a+b=4\sqrt{2}+2\sqrt{14}~~\dots\left ( 4 \right )\end{array} \)
By (3) and (4)
\(\begin{array}{l}\Rightarrow a+\frac{\sqrt{7}}{2} a=4\sqrt{2}+2\sqrt{14}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{a\left ( 2+\sqrt{7} \right )}{2}=2\sqrt{2}\left ( 2+\sqrt{7} \right ) \end{array} \)
\(\begin{array}{l}\Rightarrow a=4\sqrt{2} \end{array} \)
⇒a2 = 32 and b2 = 56
⇒ a2 + b2 = 32 + 56 = 88
9. Let \(\begin{array}{l}P_1:\vec{r}\cdot\left ( 2\hat{i}+\hat{j}-3\hat{k} \right )=4\end{array} \)
be a plane. Let P2 be another plane which passes through the points (2, –3, 2), (2, –2, –3) and (1, –4, 2). If the direction ratios of the line of intersection of P1 and P2 be 16, α, β, then the value of α + β is equal to _______.
Answer (28)
Sol. Direction ratio of normal to P1≡< 2, 1, – 3 >
and that of
\(\begin{array}{l}P_2\equiv\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\0 & 1 & -5 \\-1 & -2 & 5 \\\end{vmatrix}=-5\hat{i}-\hat{j}\left ( -5 \right )+\hat{k}\left ( 1 \right )\end{array} \)
i.e.< –5, 5, 1 >
d.r’s of line of intersection are along vector
\(\begin{array}{l}\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\2 & 1 & -3 \\-5 & 5 & 1 \\\end{vmatrix}=\hat{i}\left ( 16 \right )-\hat{j}\left ( -13 \right )+\hat{k}\left ( 15 \right )\end{array} \)
i.e.< 16, 13, 15 >
∴ α + β = 13 + 15 = 28
10. Let b1b2b3b4 be a 4-element permutation with bi{1, 2, 3,…..,100} for 1 ≤i≤ 4 and bi ≠bj for i ≠ j, such that either b1, b2, b3 are consecutive integers or b2, b3, b4 are consecutive integers. Then the number of such permutations b1b2b3b4 is equal to _______.
Answer (18915)
Sol. There are 98 sets of three consecutive integer and 97 sets of four consecutive integers.
Using the principle of inclusion and exclusion,
Number of permutations of b1b2b3b4 = Number of permutations when b1b2b3 are consecutive + Number of permutations when b2b3b4 are consecutive – Number of permutations when b1b2b3b4 are consecutive
=97 × 98 + 97 × 98 – 97 = 97 × 195 = 18915.
JEE Main 2022 June 29th Paper & Solutions – Shift 1
JEE Main 2022 June 29 Shift 1 Question Paper – Physics Solutions
JEE Main 2022 June 29 Shift 1 Question Paper – Chemistry Solutions
JEE Main 2022 June 29 Shift 1 Question Paper – Maths Solutions
Frequently Asked Questions -FAQs
Q1
What is the difficulty level of the Shift 1 JEE Main 2022 Maths June 29 question paper?
We can say that the difficulty level of the Shift 1 JEE Main 2022 Maths June 29 question paper was 1.9 out of 3.
Q2
How many questions are there in section B of the JEE Main 2022 Shift 1 June 29 Maths question paper?
There are 10 questions in section B of the JEE Main 2022 Shift 1 June 29 Maths question paper.
Q3
Is there a choice in section B of the JEE Main 2022 June 29 Shift 1 Maths question paper?
Yes. The choice is given in section B of the JEE Main 2022 June 29 Shift 1 Maths question paper. Students have to do only 5 out of 10 questions.
Q4
What type of questions were asked from Complex numbers in the JEE Main 2022 June 29 Maths Shift 1 question paper?
The questions from Complex numbers in the JEE Main 2022 June 29 Maths Shift 1 question paper were medium level.
Q5
Was the JEE Main 2022 June 29 Shift 1 Maths question paper difficult compared to JEE Main 2022 June 29 Shift 1 Physics and Chemistry?
Yes. The JEE Main 2022 June 29 Shift 1 Maths question paper was difficult compared to JEE Main 2022 June 29 Shift 1 Physics and Chemistry.



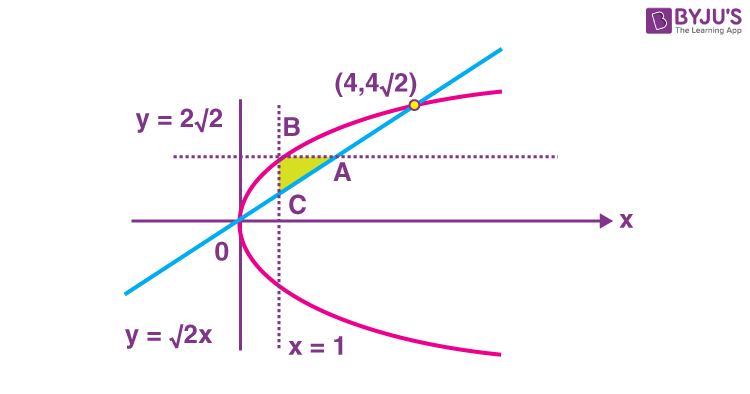


















Comments