The JEE Main 2022 July 28 – Shift 1 Physics Question Paper with Solutions is given on this page. Practising question papers is one of the best methods to crack any entrance exams. Students are advised to solve and revise JEE Main 2022 question papers so that they can score more marks in the upcoming entrance exams. Subject experts at BYJU’S have carefully prepared error-free JEE Main 2022 answer keys so that students can analyse their performance and determine their scores. Check out the JEE Main 2022 July 28 – Shift 1 Physics Question Paper with Solutions given below.
JEE Main 2022 28th July Shift 1 Physics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. The dimensions of \(\begin{array}{l}\left(\frac{B^2}{\mu_0}\right)\ \text{will be}\end{array} \)
\(\begin{array}{l}\left(\text{if} ~\mu_0 :\text{ permeability of free space and B : magnetic field}\right)\end{array} \)
\(\begin{array}{l}\left(A\right) \left[ML^2T^{–2}\right]\\ \left(B\right) \left[MLT^{–2}\right]\\ \left(C\right) \left[ML^{–1}T^{–2}\right]\\ \left(D\right) \left[ML^2T^{–2}A^{–1}\right]\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\left[\frac{B^2}{\mu_0}\right]= \text{[Energy density]}\end{array} \)
\(\begin{array}{l}=\frac{ML^2T^{-2}}{L^3}=ML^{-1}T^{-2}\end{array} \)
2. An NCC parade is going at a uniform speed of 9 km/h under a mango tree on which a monkey is sitting at a height of 19.6 m. At any particular instant, the monkey drops a mango. A cadet will receive the mango whose distance from the tree at time of drop is (Given g = 9.8 m/s2)
(A) 5 m
(B) 10 m
(C) 19.8 m
(D) 24.5 m
Answer (A)
Sol.
\(\begin{array}{l}H=\frac{1}{2}gt^2\\ 19.6 = 4.9 t^2\\ t = 2 \text{s}\end{array} \)
\(\begin{array}{l}D=9\times \frac{5}{18}\times 2 = 5 \text{ m}\end{array} \)
3. In two different experiments, an object of mass 5 kg moving with a speed of 25 ms–1 hits two different walls and comes to rest within (i) 3 second, (ii) 5 seconds, respectively.
Choose the correct option out of the following:
(A) Impulse and average force acting on the object will be same for both the cases.
(B) Impulse will be same for both the cases but the average force will be different.
(C) Average force will be same for both the cases but the impulse will be different.
(D) Average force and impulse will be different for both the cases.
Answer (B)
Sol. ΔP = impulse = same since acceleration is different force acting will be different.
4. A balloon has mass of 10 g in air. The air escapes from the balloon at a uniform rate with velocity
4.5 cm/s. If the balloon shrinks in 5 s completely. Then, the average force acting on that balloon will be (in dyne).
(A) 3
(B) 9
(C) 12
(D) 18
Answer (B)
Sol.
\(\begin{array}{l}F_{\text{avg}} = \mu \times v_{\text{rel}}\end{array} \)
\(\begin{array}{l}=\frac{10}{5}\times 4.5 = 9\end{array} \)
5. If the radius of Earth shrinks by 2% while its mass remains the same. The acceleration due to gravity on the earth’s surface will approximately
(A) Decrease by 2%
(B) Decrease by 4%
(C) Increase by 2%
(D) Increase by 4%
Answer (D)
Sol.
\(\begin{array}{l}g=\frac{GM}{R^2}\end{array} \)
\(\begin{array}{l}\frac{\Delta R}{R}\times 100 = -2\end{array} \)
\(\begin{array}{l}\frac{\Delta g}{g}= -\frac{2\Delta R}{R}=4\%\\ \text{Increase by}~ 4\%\end{array} \)
6. The force required to stretch a wire of cross-section 1 cm2 to double its length will be:
\(\begin{array}{l}\left(\text{Given Young’s modulus of the wire} = 2 \times 10^{11} ~\text{N/m}^2\right)\end{array} \)
\(\begin{array}{l}\left(A\right) 1 \times 10^7~ \text{N}\\ \left(B\right) 1.5 \times 10^7 ~\text{N}\\ \left(C\right) 2 \times 10^7~ \text{N}\\ \left(D\right) 2.5 \times 10^7 ~\text{N}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}A = 1~ \text{cm}^2\end{array} \)
\(\begin{array}{l}Y = \frac{Fl}{A \Delta l}\end{array} \)
\(\begin{array}{l}F = \frac{YA\Delta l}{l} = \frac{2 \times 10 ^{11} \times 10^{-4}\times l}{l}\\ = 2 \times 10^{7} ~\text{N}\end{array} \)
7. A Carnot engine has efficiency of 50%. If the temperature of the sink is reduced by 40°C, its efficiency increases by 30%. The temperature of the source will be:
(A) 166.7 K
(B) 255.1 K
(C) 266.7 K
(D) 367.7 K
Answer (C)
Sol.
\(\begin{array}{l}1-\frac{T_L}{T_H}=0.5~~~~~~~~~~~~~~…(1)\end{array} \)
\(\begin{array}{l}1-\frac{T_L-40}{T_H}=0.65~~~~~~~~~~~…(2)\end{array} \)
\(\begin{array}{l}\Rightarrow T_H = \frac{800}{3} \text{ K} \simeq 266.7 \text{ K} \end{array} \)
8. Given below are two statements :
Statement I : The average momentum of a molecule in a sample of an ideal gas depends on temperature.
Statement II : The rms speed of oxygen molecules in a gas is v. If the temperature is doubled and the oxygen molecules dissociate into oxygen atoms, the rms speed will become 2v.
In the light of the above statements, choose the correct answer from the options given below:
(A) Both Statement I and Statement II are true
(B) Both Statement I and Statement II are false
(C) Statement I is true but Statement II is false
(D) Statement I is false but Statement II is true
Answer (D)
Sol.
\(\begin{array}{l} \text{Average momentum} =\left< \vec{P}\right> = 0\end{array} \)
\(\begin{array}{l}v_{\text{rms}}=\sqrt{\frac{3RT}{M}}\end{array} \)
If temperature is doubled and oxygen atoms are used then
\(\begin{array}{l}v’_{\text{rms}}=\sqrt{\frac{3R(2T)}{M/2}}=4v_{\text{rms}}\end{array} \)
9. In the wave equation
\(\begin{array}{l}y=0.5\sin \frac{2\pi}{\lambda}(400t-x)\text{m}\end{array} \)
the velocity of the wave will be :
\(\begin{array}{l}\left(A\right) 200~\text{m/s}\\\left(B\right) 200\sqrt{2}~ \text{ m/s} \\\left(C\right)400 ~\text{m/s}\\ \left(D\right) 400\sqrt{2} ~\text{ m/s}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}v_{\text{wave}}= \left|\frac{\text{Coefficient of }t}{\text{Coefficient of } x}\right|\end{array} \)
\(\begin{array}{l}=\frac{400}{1}=400 \text{ m/s}\end{array} \)
10. Two capacitors, each having capacitance 40 μF are connected in series. The space between one of the capacitors is filled with dielectric material of dielectric constant K such that the equivalence capacitance of the system became 24 μF. The value of K will be :
(A) 1.5
(B) 2.5
(C) 1.2
(D) 3
Answer (A)
Sol.
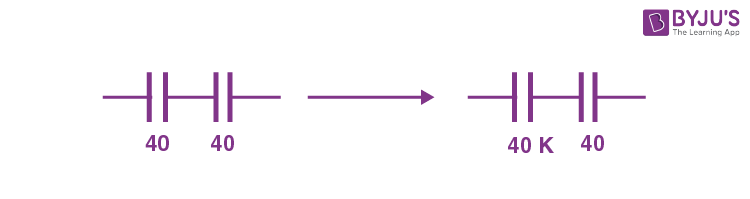
\(\begin{array}{l}\frac{40K \times 40}{40K + 40}= 24\end{array} \)
\(\begin{array}{l}40K = 24 \left(K + 1\right)\\ 40K = 24K + 24\\ 16K = 24\end{array} \)
\(\begin{array}{l}K = \frac{24}{16}=\frac{3}{2}=1.5\end{array} \)
11. A wire of resistance R1 is drawn out so that its length is increased by twice of its original length. The ratio of new resistance to original resistance
is :
(A) 9 : 1
(B) 1 : 9
(C) 4 : 1
(D) 3 : 1
Answer (A)
Sol.
R = ρl/A …(1)
Al = constant …(2)
⇒ R ∝ l2
⇒ Ratio = 32 = 9
12. The current sensitivity of a galvanometer can be increased by :
(A) Decreasing the number of turns
(B) Increasing the magnetic field
(C) Decreasing the area of the coil
(D) Decreasing the torsional constant of the spring
Choose the most appropriate answer from the options given below :
(A) (B) and (C) only
(B) (C) and (D) only
(C) (A) and (C) only
(D) (B) and (D) only
Answer (D)
Sol.
\(\begin{array}{l}NiAB = k\theta\\ \Rightarrow \frac{\theta}{i}=\frac{NAB}{k}\end{array} \)
\(\begin{array}{l}\Rightarrow\text{Sensitivity increases if} B\uparrow \text{ and } k\downarrow\end{array} \)
13. As shown in the figure, a metallic rod of linear density 0.45 kg m–1 is lying horizontally on a smooth inclined plane which makes an angle of 45° with the horizontal. The minimum current flowing in the rod required to keep it stationary, when 0.15 T magnetic field is acting on it in the vertical upward direction, will be : {Use g = 10 m/s2}
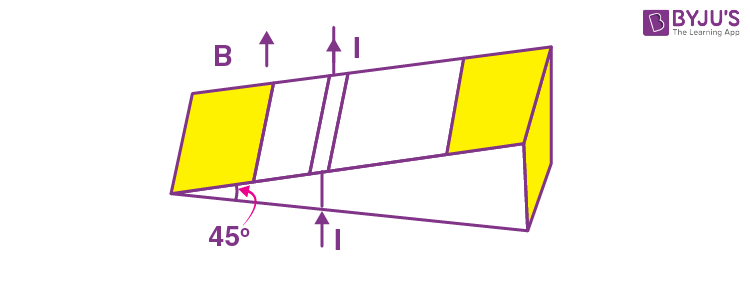
(A) 30 A
(B) 15 A
(C) 10 A
(D) 3 A
Answer (A)
Sol.
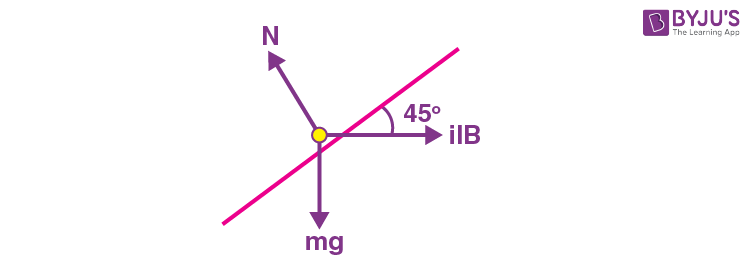
\(\begin{array}{l}mg \times \frac{1}{\sqrt{2}}=\frac{ilB}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow i = \frac{mg}{Bl}\end{array} \)
\(\begin{array}{l}=\frac{0.45 \times 10}{0.15}= 30 \text{ A}\end{array} \)
14. The equation of current in a purely inductive circuit is 5sin(49 πt – 30°). If the inductance is 30 mH then the equation for the voltage across the inductor, will be :
\(\begin{array}{l}\left\{ \text{Let } \pi = \frac{22}{7}\right\}\end{array} \)
\(\begin{array}{l}\left(A\right) 1.47~sin\left(49 ~\pi t – 30^\circ \right)\\ \left(B\right) 1.47~sin\left(49~ \pi t + 60^\circ \right)\\ \left(C\right) 23.1~sin\left(49 ~\pi t – 30^\circ \right)\\ \left(D\right) 23.1~sin\left(49 ~\pi t + 60^\circ \right)\end{array} \)
Answer (D)
Sol.
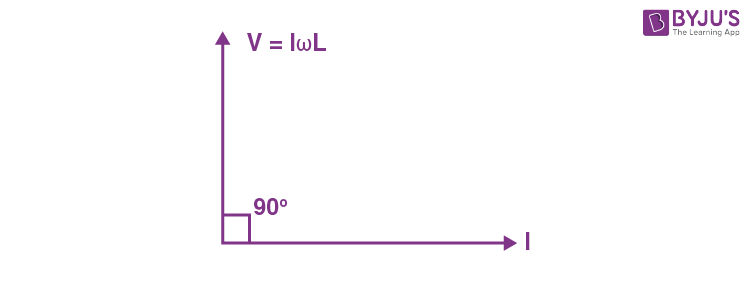
\(\begin{array}{l}V\left(t\right) = I\omega L sin\left(49 \pi t – 30 ^\circ + 90 ^\circ \right)\end{array} \)
\(\begin{array}{l}=5 \times 49 \pi \times \frac{30}{1000}\sin(49\pi t + 60^{\circ})\end{array} \)
\(\begin{array}{l}= 23.1sin\left(49\pi t + 60^\circ\right)\end{array} \)
15. As shown in the figure, after passing through the medium 1. The speed of light v2 in medium 2 will
be :
\(\begin{array}{l}\left(\text{Given} ~c = 3 \times 10^8 ~\text{ms}^{-1}\right)\end{array} \)
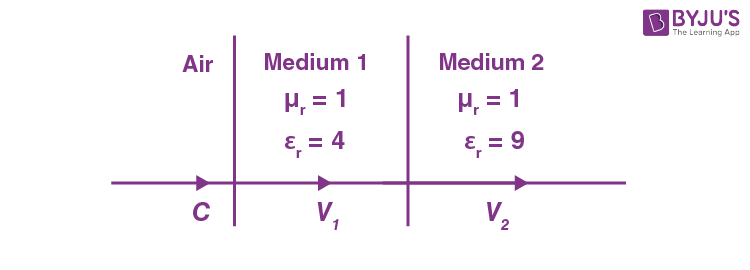
\(\begin{array}{l}\left(A\right) 1.0 \times 10^8~ \text{ms}^{-1}\\ \left(B\right) 0.5 \times 10^8 ~\text{ms}^{-1}\end{array} \)
\(\begin{array}{l}\left(C\right) 1.5 \times 10^8 ~\text{ms}^{-1}\\\left(D\right) 3.0 \times 10^8 ~\text{ms}^{-1}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l}V = \frac{1}{\sqrt{\mu \varepsilon}} = \frac{1}{\sqrt{\mu_r \varepsilon_r \mu_0 \varepsilon_0}}\end{array} \)
\(\begin{array}{l}\Rightarrow V_2 = \frac{c}{\sqrt{9}}=10^8 \text{ m/s}\end{array} \)
16. In normal adjustment, for a refracting telescope, the distance between objective and eye piece is 30 cm. The focal length of the objective, when the angular magnification of the telescope is 2, will be:
(A) 20 cm
(B) 30 cm
(C) 10 cm
(D) 15 cm
Answer (A)
Sol.
\(\begin{array}{l}\because m = \frac{f_o}{f_e}\end{array} \)
\(\begin{array}{l}\Rightarrow 2 = \frac{f_o}{f_e}~~~~~~~~\cdots(i)\end{array} \)
\(\begin{array}{l}\text{and,} l = f_o + f_e \Rightarrow 30 = f_o + f_e …\left(ii\right) \end{array} \)
\(\begin{array}{l}\Rightarrow 30 = f_o + \frac{f_o}{2} \end{array} \)
\(\begin{array}{l}\Rightarrow 30 \times \frac{2}{3}=f_o\end{array} \)
\(\begin{array}{l}\Rightarrow f_o = 20 ~\text{cm}\end{array} \)
17. The equation λ = (1.227/x) nm can be used to find the de- Broglie wavelength of an electron.
In this equation x stands for :
Where, m = mass of electron
P = momentum of electron
K = Kinetic energy of electron
V = Accelerating potential in volts for electron
\(\begin{array}{l}(\text{A})\ \sqrt{mK}\end{array} \)
\(\begin{array}{l}(\text{B})\ \sqrt{P}\end{array} \)
\(\begin{array}{l}(\text{C})\ \sqrt{K}\end{array} \)
\(\begin{array}{l}(\text{D})\ \sqrt{V}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\because \lambda = \frac{1.227}{\sqrt{V}} \text{ nm}\end{array} \)
\(\begin{array}{l}\Rightarrow x = \sqrt{V}\end{array} \)
18. The half life period of a radioactive substance is 60 days. The time taken for (7/8)th of its original mass to disintegrate will be :
(A) 120 days
(B) 130 days
(C) 180 days
(D) 20 days
Answer (C)
Sol.
\(\begin{array}{l}\because N = \frac{N_0}{\frac{t}{2^{T_{1/2}}}}\end{array} \)
\(\begin{array}{l}\Rightarrow 2^{\frac{t}{^{T_{1/2}}}} = \frac{N_0}{N}=\frac{N_0}{\left(\frac{N_0}{8}\right)}\end{array} \)
\(\begin{array}{l}\Rightarrow 2^{\frac{t}{^{T_{1/2}}}} = 8 = 2^3\end{array} \)
\(\begin{array}{l}\Rightarrow t = 3 \times T_{1/2} = 3 \times 60\\= 180 ~\text{days} \end{array} \)
19. Identify the solar cell characteristics from the following options :
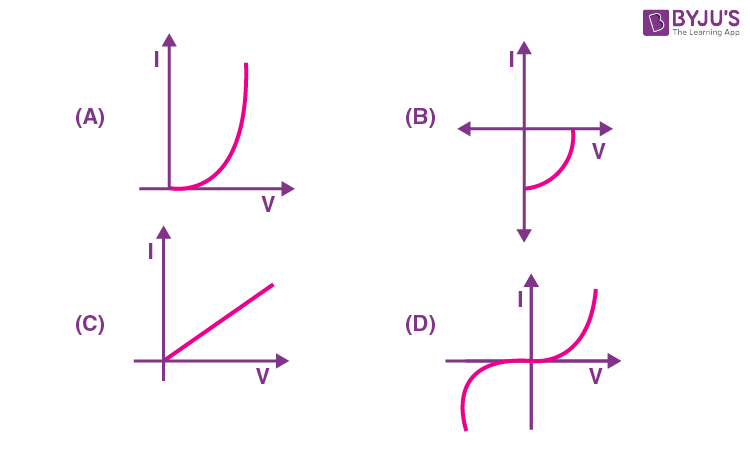
Answer (B)
Sol. Solar cell characteristics
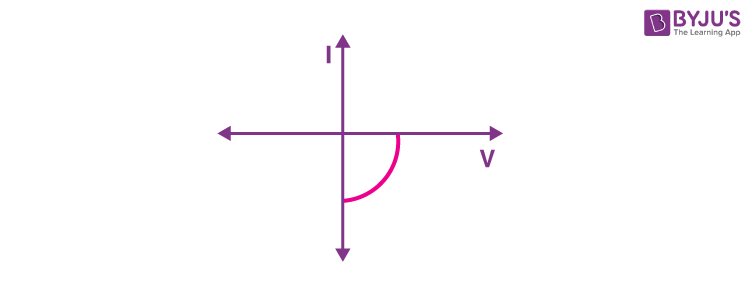
20. In the case of amplitude modulation to avoid distortion the modulation index (μ) should be :
\(\begin{array}{l}\left(A\right) \mu \le 1 \\ \left(B\right) \mu \geq 1\\ \left(C\right) \mu = 2\\ \left(D\right) \mu = 0 \end{array} \)
Answer (A)
Sol. For effective modulation,
\(\begin{array}{l} \mu \le 1 \end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Projection of \(\begin{array}{l}2\hat{i}+4\hat{j}-2\hat{k} \text{ on } \hat{i}+ 2\hat{j}-\alpha \hat{k}\end{array} \)
is zero. Then, the value of α will be ________.
Answer (5)
Sol.
\(\begin{array}{l}\vec{A}=2\hat{i}+4\hat{j}-2\hat{k}\end{array} \)
\(\begin{array}{l}\vec{B}=\hat{i}+2\hat{j}+\alpha\hat{k}\end{array} \)
\(\begin{array}{l}\vec{A} \cdot \vec{B}=0\end{array} \)
, as \(\begin{array}{l}\vec{A}\end{array} \)
should be perpendicular to \(\begin{array}{l}\vec{B}\end{array} \)
\(\begin{array}{l}\Rightarrow 2 + 8 – 2\alpha = 0\\ \alpha = 5 \end{array} \)
2. A freshly prepared radioactive source of half life 2 hours 30 minutes emits radiation which is 64 times the permissible safe level. The minimum time, after which it would be possible to work safely with source, will be _______ hours.
Answer (15)
Sol.
\(\begin{array}{l}T_{1/2} = 150 \text{ minutes}\end{array} \)
A0 = 64 x, where x is safe limit
\(\begin{array}{l}x=64x \times 2^{- \frac{n}{T_{1/2}}}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{1}{64}=2^{-\frac{n}{T_{1/2}}}\end{array} \)
\(\begin{array}{l}\text{or } \frac{n}{T_\frac{1}{2}} =6\end{array} \)
\(\begin{array}{l}\Rightarrow n = 6 \times 150~ \text{minutes}\\ = 15 ~\text{hours}\end{array} \)
3. In a Young’s double slit experiment, a laser light of 560 nm produces an interference pattern with consecutive bright fringes’ separation of 7.2 mm. Now another light is used to produce an interference pattern with consecutive bright fringes’ separation of 8.1 mm. The wavelength of second light is ________ nm.
Answer (630)
Sol.
\(\begin{array}{l}\lambda = 560 \times 10^{–9}\\ B_1 = 7.2 \times 10^{–3}\\ B_2 = 8.1 \times 10^{–3}\end{array} \)
\(\begin{array}{l}\frac{B_1}{B_2}=\frac{\lambda_1}{\lambda_2}\end{array} \)
\(\begin{array}{l}\Rightarrow \lambda_2 = \frac{560 \times 10 ^{-9} \times 8.1 \times 10^{-3}}{7.2 \times 10^{-3}}\end{array} \)
\(\begin{array}{l} = 6.3 \times 10^{-7} ~\text{m}\\ = 630~ \text{nm}\end{array} \)
4. The frequencies at which the current amplitude in an LCR series circuit becomes 1/√2 times its maximum value, are \(\begin{array}{l} 212~ \text{rad s}^{-1} ~\text{and}~ 232 ~\text{rad s}^{-1}\end{array} \)
. The value of resistance in the Question: circuit is R = 5 Ω. The self-inductance in the circuit is _____ mH.
Answer (250)
Sol.
\(\begin{array}{l}\frac{i}{i_{\text{max}}} = \frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}=\frac{V_0/Z}{V_0/R}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{R}{Z} = \frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\text{and } \frac{1}{212C}-212L = 232L – \frac{1}{232C}\end{array} \)
\(\begin{array}{l}\text{so } 212L = \frac{1}{232C}\end{array} \)
\(\begin{array}{l}\text{so } \frac{R}{\sqrt{R^2 + \left(232L + \frac{1}{232C}\right)^2}}=\frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}\frac{R^2}{R^2 + (20 L)^2}=\frac{1}{2}\end{array} \)
\(\begin{array}{l}400 L^2 = R^2\end{array} \)
\(\begin{array}{l}L = \frac{5}{20}\end{array} \)
\(\begin{array}{l}H=\frac{5}{20}\times 1000 \text{ mH}\\= 250 \text{mH} \end{array} \)
5. As shown in the figure, a potentiometer wire of resistance 20 Ω and length 300 cm is connected with resistance box (R.B.) and a standard cell of emf 4 V. For a resistance ‘R‘ of resistance box introduced into the circuit, the null point for a cell of 20 mV is found to be 60 cm. The value of ‘R ‘ is Ω.
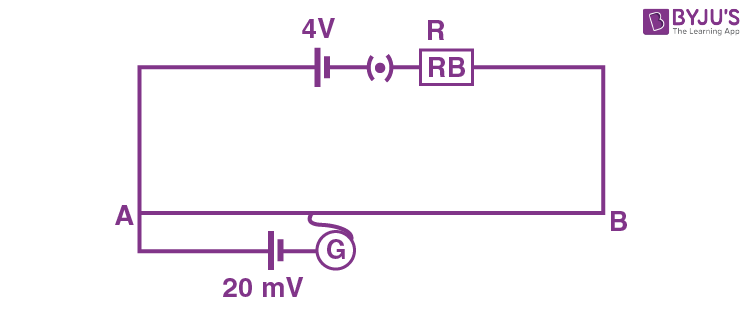
Answer (780)
Sol.
\(\begin{array}{l}l = 3\text{m}, R_W = 20 ~\Omega \\\varepsilon_0 = 4\text{V}\end{array} \)
\(\begin{array}{l}\frac{4 \times 20}{20 + R}\times \frac{60}{300} = 20 \times 10^{-3}\end{array} \)
\(\begin{array}{l}\frac{4}{20+R}=5\times 10^{-3}\end{array} \)
\(\begin{array}{l}20 + R = 800\\ R =780~ \Omega\end{array} \)
6. Two electric dipoles of dipole moments \(\begin{array}{l}1.2 \times 10^{-30}~\text{C-m and~} 2.4 \times 10^{-30}~ \text{C-m}\end{array} \)
are placed in two different uniform electric fields of strength \(\begin{array}{l}5 \times 10^4 ~\text{NC}^{-1} ~\text{and~} 15 \times 10^4 ~\text{NC}^{-1}\end{array} \)
respectively. The ratio of maximum torque experienced by the electric dipoles will be 1/x. The value of x is _______.
Answer (6)
Sol.
\(\begin{array}{l}\frac{\rho_1}{\rho_2}=\frac{\mu_1B_1\sin 90}{\mu_2 B_2 \sin 90}\end{array} \)
\(\begin{array}{l}=\frac{1.2 \times 10^{-30} \times 5 \times 10^4}{2.4 \times 10^{-30}\times 15 \times 10^4}\end{array} \)
\(\begin{array}{l}=\frac{1}{6}\end{array} \)
7. The frequency of echo will be _______ Hz if the train blowing a whistle of frequency 320 Hz is moving with a velocity of 36 km/h towards a hill from which an echo is heard by the train driver. Velocity of sound in air is 330 m/s.
Answer (340)
Sol.
\(\begin{array}{l}v_s=36 \times \frac{5}{18} = 10 \text{ m/sec}\end{array} \)
\(\begin{array}{l}f=\frac{v+v_s}{v-v_s}f_0\end{array} \)
\(\begin{array}{l}=\frac{340}{320}\times 320= 340 ~\text{Hz} \end{array} \)
8. The diameter of an air bubble which was initially 2 mm, rises steadily through a solution of density \(\begin{array}{l}1750 ~\text{kg m}^{-3} ~\text{at the rate of}~ 0.35 ~\text{cms}^{-1}. \end{array} \)
The coefficient of viscosity of the solution is _______ poise (in nearest integer). (The density of air is negligible).
Answer (11)
Sol.
\(\begin{array}{l}F = 6\pi \eta rv\end{array} \)
\(\begin{array}{l}\frac{4}{3}\pi r^3 \rho_lg = 6\pi \eta rv\end{array} \)
\(\begin{array}{l}\eta = \frac{2r^2\rho_lg}{v}\end{array} \)
\(\begin{array}{l}=\frac{2\times (2 \times 10^{-3})^2 \times 1750 \times 10}{9\times 3.5 \times 10^{-3}\times 4}= 11 \text{poise} \end{array} \)
9. A block of mass ‘m’ (as shown in figure) moving with kinetic energy E compresses a spring through a distance 25 cm when, its speed is halved. The value of spring constant of used spring will be nE Nm–1 for n = _______.
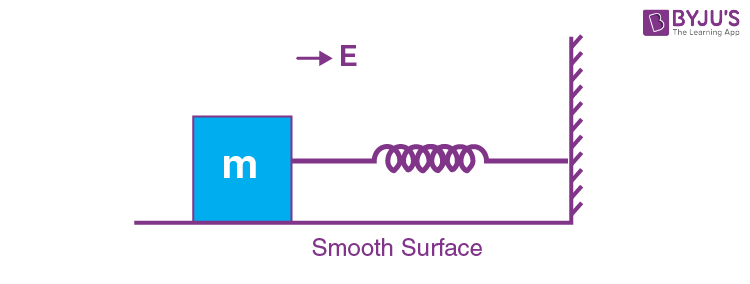
Answer (24)
Sol.
ΔKE = Wall
\(\begin{array}{l} \text{So } \frac{E}{4}-E = -\frac{1}{2}K \times (0.25)^2\end{array} \)
\(\begin{array}{l}\frac{3E}{4}=\frac{1}{2}K \times\frac{1}{16}\\ K = 24E\end{array} \)
10. Four identical discs each of mass ‘M’ and diameter ‘a’ are arranged in a small plane as shown in the figure. If the moment of inertia of the system about OO’ is (x/4) Ma2. Then, the value of x will be _______.
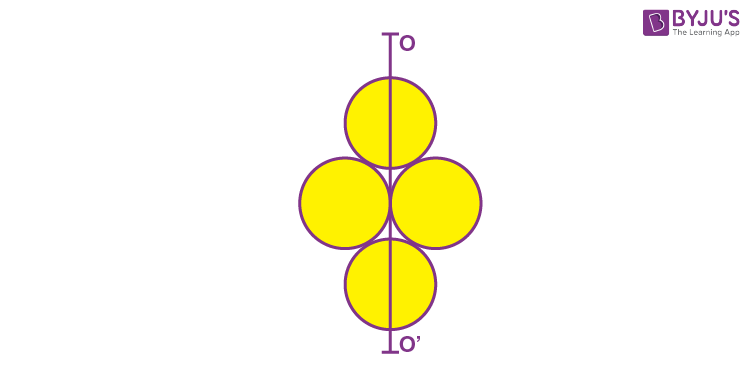
Answer (3)
Sol.
\(\begin{array}{l}I = 2\times \left( \frac{M\left( \frac{a}{2}\right)^2}{4} \right)+ 2 \times \left( \frac{M\left(\frac{a}{2}\right)^2}{4} + M \left(\frac{a}{2}\right)^2\right)\end{array} \)
\(\begin{array}{l}=\frac{Ma^2}{8}+\frac{5Ma^2}{8}\end{array} \)
\(\begin{array}{l}=\frac{6Ma^2}{8}=\frac{3}{4}Ma^2\end{array} \)
JEE Main 2022 July 28th Shift 1 Paper Analysis





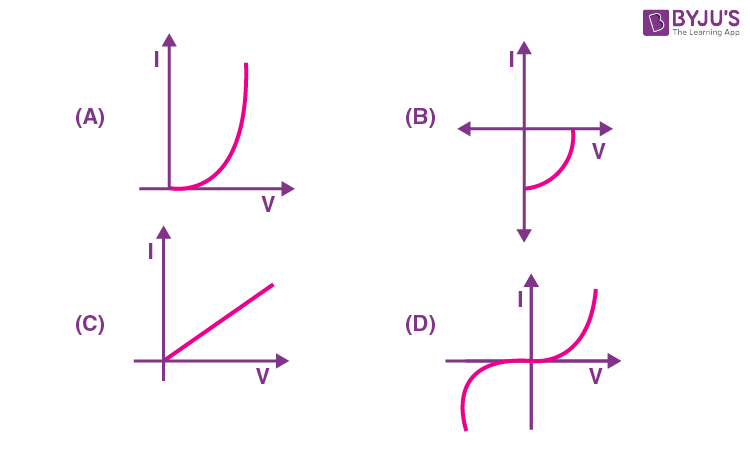













Comments