How to Find Moment of Inertia of T Section (Solved Example)

Moment of Inertia is the quantity that expresses an object’s resistance to change its state of rotational motion. The moment of inertia of a T section is calculated by considering it as 2 rectangular segments. The moment of inertia is separately calculated for each segment and put in the formula to find the total moment of inertia.

How to Find Moment of inertia of “T” section

The following steps should be followed to find the moment of inertia of the T section.

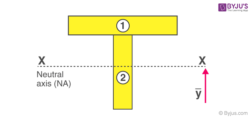
Moment of inertia of T-section

Step 1: The beam sections should be segmented into parts

The T beam section should be divided into smaller sections. The moment of inertia must be calculated for the smaller segments. Here the section is divided into two rectangular segments.

Step 2: Mark the neutral axis

The neutral axis is the horizontal line passing through the centre of mass. The centre of mass is calculated using the following formula

Y_c = ΣY_iA_i/ΣA_i

Y_iis the centre of mass of the individual rectangle

A_iis the area of the individual rectangle

Step 3: Calculating the Moment of Inertia

Using the parallel axis theorem the total momentum is calculated as

\(\begin{array}{l}I_{total}=\sum (\bar{I_{i}}+A_{i}d_{i}^{2})\end{array} \)

where,

\(\begin{array}{l}(\bar{I_{i}})\ \text{is the inertia of the individual segment about its own centroid axis.}\end{array} \)

A_iis the area of the individual segment

d_i is the vertical distance from the centroid of the segment.

The moment of inertia of each of the rectangular parts must be calculated. The moment of inertia equation of a rectangle about its centroid axis is

\(\begin{array}{l}\bar{I} = \frac{1}{12}bh^{3}\end{array} \)

Where,

b is the base of the rectangle

h is the height of the rectangle

Example

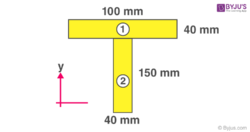
Moment of inertia T section 2

Let us understand the above equation with an example.

Finding the centre of mass of the T section

Y_c = ΣY_iA_i/ΣA_i

={[(150 + (40/2))(40 x 100)] + [(150/2) + (150 x40)]} / {[(40x 100) + (150 x40)]

=[(170 x 4000) + (75 x 600)]/ [4000 + 6000]

= 113 mm

Moment of inertia of T section,

\(\begin{array}{l}I_{total}=\sum (\bar{I_{i}}+A_{i}d_{i}^{2})\end{array} \)

Where I_i is the moment of inertia of the individual segments

A_iis the area of the individual segments

d_i is the vertical distance from the centroid of the segment

The moment of inertia equation of a rectangle about its centroid axis is given by

\(\begin{array}{l}\bar{I} = \frac{1}{12}bh^{3}\end{array} \)

Where,

b is the base of the rectangle

h is the height of the rectangle

\(\begin{array}{l}(\bar{I_{1}}) = \frac{1}{12}\times 100\times (40)^3\end{array} \)

= 533,333 mm⁴

\(\begin{array}{l}(\bar{I_{2}})=\frac{1}{12}\times 40\times (150)^3\end{array} \)

= 1.125 x 10⁷ mm⁴

\(\begin{array}{l}I_{total}=\sum (\bar{I_{i}}+A_{i}d_{i}^{2})\end{array} \)

= [(533,333 + 4000(170 – 113)²] + [(1.125 x 10⁷) + 6000(113 – 75)²]

I_total= 3.3443 x 10⁷ mm⁴

Parallel Axis Theorem

Comments

Leave a Comment Cancel reply