The centre of mass is a unique position of an object or a system of objects where the entire mass of the system is concentrated. The motion of this unique point is identical to the motion of a single-particle whose mass is equal to the sum of all individual particles of the system. The method to find the centre of mass of a semicircular ring is discussed in this page.
How to Find Centre of Mass of Semicircular Ring
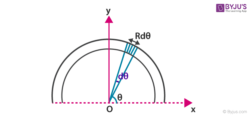
We are taking a half ring, which has a uniformly distributed mass with a radius R. The centre of mass of the ring will lie on the vertical line passing through the centre of the ring. The vertical line is considered as the y-axis. The horizontal line seen in the figure is the x-axis.
We are considering an elemental mass dM on the ring. The element is taken at an angle θ from the y-axis, it has an angular width of dθ and a linear width of Rdθ.
The mass of element dM = (M/π)dθ
The y-coordinate of dM is, y = Rcosθ
The y-coordinate of the centre of mass, yc = (1/M)ഽydM
Integrating the above equation, we get
y = (R/π)[1+1] = 2R/π
The centre of mass of the ring is given by 2R/π, where R is the radius of the semicircular ring.
Centre of Mass and Collision

Frequently Asked Questions on Centre of Mass of Semicircular Ring
What is the distance between the centre and the centre of mass of a uniform semicircular ring?
The centre of mass of a uniform circular ring is at a distance of 2R/π from the centre.
R is the radius of the ring.
What is centre of mass?
Centre of mass of a system or a body is a point in the system, where if whole of the mass of the system were to be concentrated, then this point like mass would have the same type of translational motion as the system as a whole.
Can centre of mass of the body lie outside the body?
Yes. It can lie outside the body.

Comments