Critical Points Solved Examples

A point c in the domain of a function f(x) is called a critical point of f(x), if f ‘(c) = 0 or f ‘(c) does not exist. This article explains the critical points along with solved examples.

A function f, which is continuous with x in its domain, contains a critical point at point x if the following conditions hold good.

• f ’(x) = 0
• f ’(x) is undefined.

A point of a differentiable function f at which the derivative is zero can be termed a critical point.

The types of critical points are as follows:

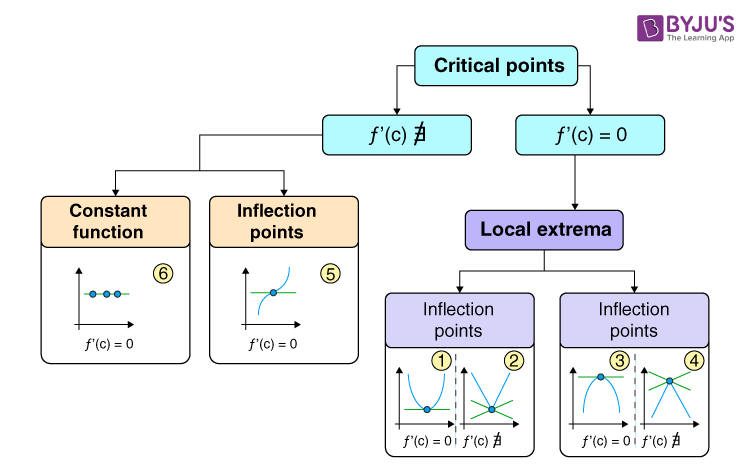
• A critical point is a local maximum if the function changes from increasing to decreasing at that point, whereas it is called a local minimum if the function changes from decreasing to increasing at that point.
• A critical point is an inflexion point if the concavity of the function changes at that point.
• If a critical point is neither of the above, then it signifies a vertical tangent in the graph of a function.

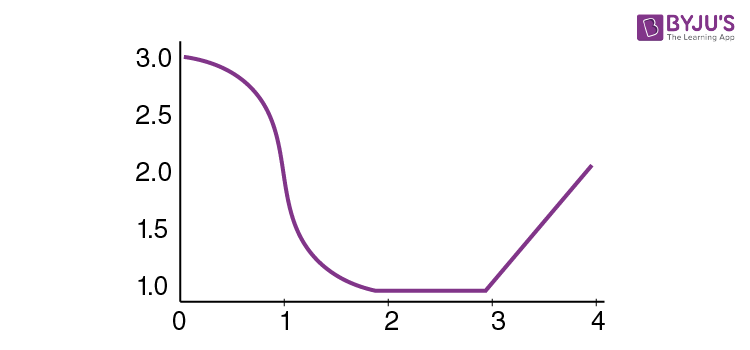
This function has critical points at x = 1 and x = 3.

Classification of critical points is explained below:

Solved Problems on Critical Points

Example 1: Find the critical points of the function f (x) = x² lnx.

Solution:

Take the derivative using the product rule:

f ′ (x) = (x² lnx)′ = 2x * ln x + x² * [1 / x] = 2x ln x + x = x (2 ln x + 1).

Determine the points where the derivative is zero:

f′(c) = 0, ⇒ c (2 ln c + 1) = 0.

The first root, c₁ = 0, is not a critical point because the function is defined only for x > 0.

Consider the second root:

2 ln c + 1 = 0, ⇒ ln c =−1 / 2,

⇒ c₂ = e ^−1/2 = 1 / √e.

Hence, c₂ = 1 / √e is a critical point of the given function.

Example 2: Local maximum and local minimum values of the function (x − 1) (x + 2)² are _______.

Solution:

f′(x) = 2 (x − 1) (x + 2) + (x + 2)² = 3x² + 6x

f′(x) = 0

x = 0, −2

f (−2) = (−2 −1) (−2 + 2)² = 0 (Maximum value), and

f (0) = (0 − 1) (0 + 2)² = −4 (Minimum value).

Example 3: Whether the given function x * √[1 − x²], (x > 0) has local maxima or minima?

Solution:

Let f (x) = x * √[1 − x²]

f′(x) = [1 − 2x²] / √[1 − x²] = 0

⇒ x = ± 1 / √2

But as x > 0, we have x = 1 / √2

Now, again f′′(x) = {(√[1 − x²] (−4x)) − ((1 − 2x²) * (− x / √[1 − x²])} / [1 − x²] = [2x³ − 3x] / (1 − x²)^3/2

⇒ f′′(1 / √2) = −ve.

Then, f (x) is maximum at x = 1 / √2.

Example 4: The area of a rectangle will be the maximum for the given perimeter when a rectangle is a ________.

Solution:

We know that the perimeter of a rectangle, S = 2 (x + y), where x and y are adjacent sides.

y = [S − 2x] / 2.

Now, the area of a rectangle,

A = xy = [x / 2] * (S − 2x) = [1 / 2] * (Sx − 2x²)

Differentiating w.r.t. x of A, we get

dA / dx = 1 / 2 (S − 4x) = 0

∴ x = S / 4 and y = S / 4

Again d²A / dx² = −ve

Hence, the area of the rectangle will be maximum when the rectangle is a square.

Example 5: If f (x) = 2x³ − 3x² − 12x + 5 and x ∈ [−2, 4], then the maximum value of the function is at what value of x?

Solution:

f′(x) = 6x² − 6x − 12

f′(x) = 0

⇒ (x − 2) (x + 1) = 0

⇒ x = −1, 2

Here, f (4) = 128 − 48 − 48 + 5 = 37

f (−1) = −2 − 3 + 12 + 5 = 12

f (2) = 16 − 12 − 24 + 5 = −15

f (−2) = −16 − 12 + 24 + 5 = 1

Therefore, the maximum value of the function is 37 at x = 4.

Example 6: The function sin x (1 + cos x) at x = π / 3 is ____________.

Solution:

Let f (x) = sin x (1 + cos x)

f′(x) = cos 2x + cos x and f′′(x) =−2 sin 2x − sin x = −(2 sin 2x + sin x)

For maximum or minimum value of f (x), f′(x) = 0

cos 2x + cos x = 0

cos x = −cos 2x

cos x = cos (π ± 2x)

∴ x = π ± 2x or x = π / 3, −π

Now, f′′(π / 3) = −2sin 2π / 3 − sin π / 3 = [−2] * [(√3) / 2] − √3 / 2 = −3√3 / 2 =−ve

Hence, f (x)is maximum at x = π / 3.

Example 7: If x + y = 10, then the maximum value of xy is __________.

Solution:

x + y =10

∴ y = 10 − x ……..(i)

Now f (x) = xy = x (10 − x) = 10x − x²

∴ f′(x) = 10 − 2x

For maximum value of f (x), f′ (x) = 0

∴ x = 5 and y = 5

So, the maximum value of xy = 5 × 5 = 25.

Example 8: The point (0, 5) is closest to the curve x² = 2y, is ________.

Solution: 

Let a point on the curve by (h, k).                    

Then, h² = 2k…..(i)

Distance = D

By (i);

So, at k = 4, function D must be minimum.                    

Then, the point will be (±2√2, 4). 

Example 9:

A)  11

B) 12

C) 10

D) 14

Solution: 

Let

Put

Again,

Now, 

Hence, the minimum value = 12.

Example 10: The function f(x) = x^-x, x ∈ R attains a maximum value at x = _____.     

A) 2

B) 3

C) 1/e

D) 1

Solution:

Differentiating w.r.t. x, 

Put dy/dx = 0

Example 11: If y = a log x + bx² + x has its extremum value at x = 1 and x = 2, then (a, b) = ______.

Solution: 

Example 12: If

Solution:

Put f'(x) = 0

8x + 2 = 0

x = -1/4