JEE Main 2024 Question Paper Solution Discussion Live JEE Main 2024 Question Paper Solution Discussion Live
× Watch Now

Derivative Examples

Consider a function which involves the change in velocity of a vehicle moving from one point to another. The change in velocity is certainly dependent on the speed and direction in which the vehicle is travelling. If the acceleration is to be calculated, then the limits of the function are essential. The theory of derivative is derived from limits. This article deals with the concept of derivatives, along with a few solved derivative examples.

Derivative Definition

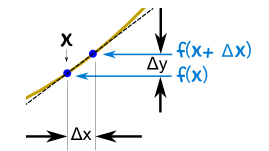
A function which denotes the rate of change of the other function can be called the derivative of that function. The method of finding a derivative can be called differentiation. It is represented as a dependent variable in terms of an independent variable through an equation. The derivative is a value which changes with respect to its input. A derivative is denoted as f’(x).

Derivative Formula

The change in the slope of a function can be termed a derivative. It is represented as follows:

derivative representation

\(\begin{array}{l}slope=\frac{change\ in\ x}{change\ in\ y}=\frac{\Delta y}{\Delta x}=\frac{dy}{dx}=\frac{f(x+\Delta x)-f(x)}{\Delta x}\end{array} \)

Related topics

Differentiation of Functions

Methods of Differentiation

Derivative Rules

Below are some important rules used to solve derivative problems.

Constant rule:

\(\begin{array}{l}\frac{d}{dx}[C] = 0\end{array} \)

Power rule:

\(\begin{array}{l}\frac{d}{dx}[x^{n}] = n \; x^{n-1}\end{array} \)

Constant multiple rule:

\(\begin{array}{l}\frac{d}{dx}[c.u] = c.\frac{du}{dx}\end{array} \)

Sum and difference rule:

\(\begin{array}{l}\frac{d}{dx}[u\pm v] = \frac{du}{dx}\pm \frac{dv}{dx}\end{array} \)

Product rule:

\(\begin{array}{l}\frac{d}{dx}[u. v] =u. \frac{dv}{dx}+v.\frac{du}{dx}\end{array} \)

Quotient rule:

\(\begin{array}{l}\frac{d}{dx}[\frac{u}{v}]=\frac{v.\frac{du}{dx}-u.\frac{dv}{dx}}{v^{2}}\end{array} \)

Some Basic Derivatives

\(\begin{array}{l}\frac{d}{dx}[x] = 1\\\frac{d}{{dx}}\sqrt x= \frac{1}{{2\sqrt x }}\\\frac{d}{{dx}}\sqrt {f(x)} = \frac{1}{{2\sqrt {f(x)} }}\frac{d}{{dx}}f(x) = \frac{1}{{2\sqrt {f(x)} }}f'(x)\\\frac{d}{{dx}}c \cdot f(x) = c\frac{d}{{dx}}f(x) = c \cdot f'(x)\\\frac{d}{{dx}}\ln x = \frac{1}{x}\\\frac{d}{{dx}}{\log _a}x = \frac{1}{{x\ln a}}\\\frac{d}{{dx}}\ln f(x) = \frac{1}{{f(x)}}\frac{d}{{dx}}f(x)\\\frac{d}{{dx}}{\log _a}f(x) = \frac{1}{{f(x)\ln a}}\frac{d}{{dx}}f(x)\\\frac{d}{{dx}}{e^x} = {e^x}\\\frac{d}{{dx}}{e^{f(x)}} = {e^{f(x)}}\frac{d}{{dx}}f(x)\\\frac{d}{{dx}}{a^x} = {a^x}\ln a\\\frac{d}{{dx}}{a^{f(x)}} = {a^{f(x)}}\ln a\frac{d}{{dx}}f(x)\\\frac{d}{{dx}}{x^x} = {x^x}(1 + \ln x)\\\frac{d}{{dx}}sinx = cosx\\\frac{d}{dx}cosx = -sinx\\\frac{d}{{dx}}tanx = sec{^2}x\\\frac{d}{{dx}}cotx = – cosec{^2}x\\\frac{d}{{dx}}secx = secx \cdot tanx\\\frac{d}{{dx}}cosec x = – co\sec x \cdot cotx\\\frac{d}{{dx}}sinhx = coshx\\\frac{d}{{dx}}coshx = sinhx\\\frac{d}{{dx}}tanhx = sec{h^2}x\\\frac{d}{{dx}}cothx =- cosec {h^2}x\\\frac{d}{{dx}}sechx =- sechx \cdot tanhx\\\frac{d}{{dx}}cosec hx =- co\sec hx \cdot cothx\\\frac{d}{dx}sin^{-1}x=\frac{1}{\sqrt{1-x^{2}}}\\\frac{d}{dx}cos^{-1}x=\frac{-1}{\sqrt {1–x^{2}}}\\\frac{d}{dx}tan^{-1}x = \frac{1}{1+{x^2}}\\\end{array} \)

Examples on Derivative for IIT JEE

Example 1: Find the derivative of x6+x3+2.

Solution:

Using the power rule (d/dx)x6 = 6x5

 (d/dx)x3 = 3x2

(d/dx)2 = 0

Hence, the derivative of x6+x3+2 = 6x5+3x2

Example 2: Solve

\(\begin{array}{l}\frac{d}{dx}tan^{-1}\frac{cosx}{1+sinx}\end{array} \)

Solution:

\(\begin{array}{l}\frac{d}{dx}tan^{-1}\frac{cosx}{1+sinx}\end{array} \)

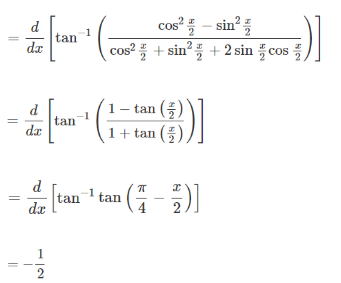
Derivative example

Example 3: What is the differential coefficient of ax + log x . sinx?

Solution:

Let y = ax + log x . sinx

Differentiating w.r.t. x, we get

dy / dx = ax loge(a) + (1 / x) sin x + log x . cos x

Example 4: If f(x) = logx (logx), then f′(x) at x = e is _____.

Solution:

f(x) = logx (logx)

= log (log x) / logx

f′(x)= 1 / x − 1 / x log (logx) / (logx)2

⇒ f′(e) = [1 / e − 0] / 1

= 1 / e

Example 5: What is the local maximum value of the function log x / x?

Solution:

Let f(x) = log x / x

⇒f′(x) = 1 / x2 − log x / x2

For maximum or minimum value of f (x), find  f′(x) = 0

f′(x) = 1 − logex / x2 = 0 or 1− logex / x2 = 0

∴ logex = 1

or x = e, which lies in (0,∞).

For x = e,

d2y / dx2 =−1 / e3, which is −ve.

Hence, y is maximum at x = e, and its maximum value = loge / e = 1 / e.

Example 6: If f(2) = 4, f′(2) = 1 then what is the value of limx→2 x f(2) − 2 f(x) / x−2?

Solution:

Given f(2) = 4, f′(2) = 1

limx→2 x f(2) − 2 f(x) / (x−2) = limx→2 x f(2) − 2 f(2) + 2 f(2) − 2 f(x) / (x−2)

[limx→2 (x−2) f(2) / (x − 2)] − [limx→2 2 f(x) − 2 f(2) / (x−2)]

f(2) − 2 limx→2 f(x) − f(2) / [x−2] = f(2) − 2 f′(2)

= 4− 2(1)

= 4−2

= 2

Example 7: In the mean-value theorem f(b) − f(a) / b−a = f′(c), if a = 0, b = 1 / 2 and f(x) = x (x−1) (x−2) , then what is the value of c?

Solution:

From the mean value theorem, f′(c)= f(b) − f(a) / b−a

Given that a=0, f(a)=0 and b = 1 / 2, f(b) = 3 / 8

f′(x) = (x−1) (x−2) + x (x−2) + x (x−1)

f′(c) = (c−1) (c−2) + c (c−2) + c (c−1)

= c2 − 3c +2 + c2 − 2c + c2 − c

f′(c) = 3c2 −6c + 2

According to the mean value theorem,

f′(c)= f(b) − f(a) / b−a

3c2 − 6c + 2= (3/8)−0 / (1/2) − 0 = 3 / 4

3c2 − 6c + 5 / 4 = 0

On solving the above equation, the value of c obtained is

c = 6 ± √[36−15] / 2 × 3

= [6 ± √21] / 6

c = [1 ± √21] / 6

Recommended Videos

Methods of Differentiation – JEE Solved Questions

Important Theorems of Differentiation for JEE

Frequently Asked Questions

Q1

Give the quotient rule of derivatives.

If u and v are two functions, then (d/dx)(u/v) = [v(du/dx) – u (dv/dx)]/v2.

Q2

What is the derivative of a constant function?

The derivative of a constant function is 0.

Q3

What is the derivative of ax?

The derivative of ax is ax log a.

Test your Knowledge on derivative
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz

Congrats!

Visit BYJU’S for all JEE related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*