The standing waves are produced due to the superposition of two identical waves with the same speed travelling in opposite directions. These waves are localised in nature, i.e., the wave is confined to a particular region between the starting point and the point of reflection of the wave. So, the energy in a loop of a standing wave cannot be transmitted across them, it is confined to the particular region. However, the energy in a loop of a standing wave will oscillate between elastic potential energy and kinetic energy of the particles of the medium.
Energy in a Loop of a Standing Wave
Let us consider a second harmonic standing wave on a string between two fixed ends. Two nodes are formed at the fixed ends, and an antinode is formed between the nodes. The part between the nodes is moving while the nodes are stationary.
When the string gets fully stretched, the energy in the string is in the form of elastic potential energy, and the kinetic energy becomes zero. However, when the string is flat, the total energy is in the form of kinetic energy and the elastic potential energy will be zero. Therefore, the total energy in the loop can be determined by finding the maximum kinetic energy of the fully stretched string.
Let us consider the wave equation of the standing wave,
y = 2Asin (kx) cos (ωt)
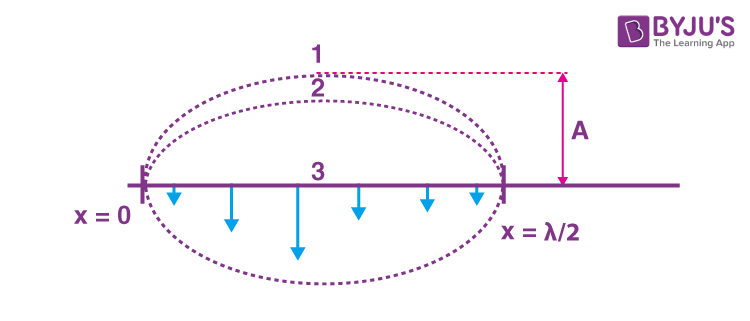
In the extreme position (1), when the string is fully stretched,
Kinetic energy = 0
Total energy = Elastic potential energy
In position (2), there is some potential energy and some kinetic energy
In position (3), when the string is flat along the mean position,
Elastic Potential energy = 0
Total energy = Kinetic energy
The energy is stored equally all along the string. Let us take a small element dx at a distance x from the node. Let the mass of the small element dx be dm.
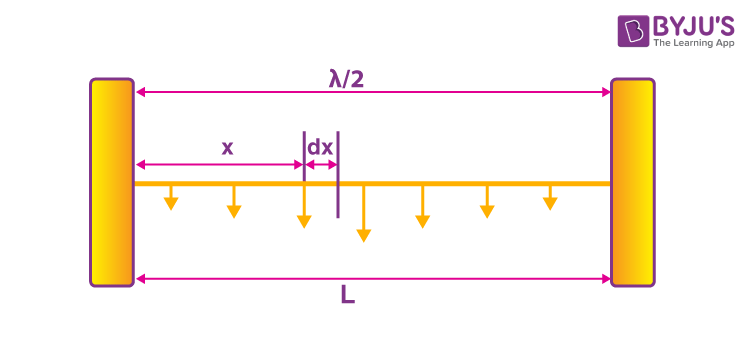
dm = μdx ——-(1)
Here, μ is the mass per unit length [ μ = M/L = M/(λ/2)]
The maximum velocity of the particle along the mean position is, v = 2Asin kx ω ——–(2)
The energy of the particle dx is
dE = (½)dmv2
Substituting the value of dm and v from equations (1) and (2),
dE = (½) μdx (2Asin kx ω)2
= (½) μdx 4A2sin2kxω2
Therefore, dE = 2A2ω2μsin2kxdx
The total energy can be determined by integrating between 0 and λ/2
Therefore, the total energy of the loop in a standing wave is
Solved Example
1. In a stationary wave, energy in a loop
- Varies instantaneously
- Changes periodically
- Depends on the type of stationary wave
- Is confined
Answer: (d) Is confined
Related Video on Energy in a Loop

Frequently Asked Questions on Energy in a Loop
Is there a transfer of energy in a standing wave?
The standing wave will not have any transfer of energy. There is no propagation of energy in a standing wave.
How is the energy transferred in a standing wave?
There is no energy transport in a standing wave because the two waves that make them up carry equal energy in opposite directions.
How is a standing wave formed?
When two waves of the same frequency travelling in the opposite direction in the same medium interfere with each other, standing waves are produced.
Mention a few characteristics of a stationary wave.
Transverse waves and longitudinal waves can form a standing wave.
The disturbance is confined to a particular region.
The position of maximum amplitude is at the antinode.
The minimum amplitude position is at the nodes.
Comments