Work energy theorem is one of the most important concepts covered in work, power and energy. It tells us how work and energy are related. We will discuss some of the most common questions about this topic.
Important Questions On Work-Energy Theorem
1. What is the statement of work energy theorem?
According to work-energy theorem, the work done by the net force on a body is equal to change in kinetic energy.
2. How can we prove work energy theorem?
We know,
Differentiating with respect to time we get,
If the resultant force makes some angle with the velocity, then
3. Steps to approach problems on work energy theorem?
Following steps should be considered:
Step-1: Draw the FBD of the object, thus identifying the forces operating on the object.
Step-2: Finding the initial and final kinetic energy.
Step-3: Equating the values according to the theorem.
4. How can we efficiently use this theorem?
The problems in which we have to calculate work done by a particular force, we can either do it using the equation of work or directly apply this theorem to get the result. For example, consider the following problem:
A block of mass 10 kg starts moving up the incline with 20 m/s. It reaches the top and comes back to its initial position and stops. What is the work done by friction in the whole process?
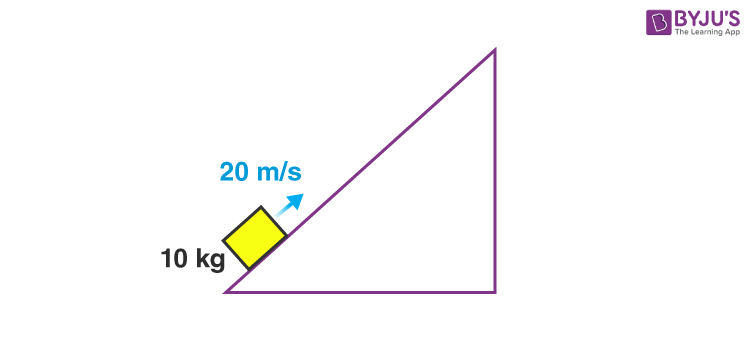
If we want to use the formula of work then we need the coefficient of friction to calculate frictional force. But that is not given. So let’s try to use work-energy theorem. Forces acting on the block are gravity, normal reaction, and frictional force. So,
Here, WN is zero as force is always perpendicular to displacement. Being a conservative force Wg is zero as the body returns to its initial position. Also,
Hence the work done by friction is negative.
To learn more about different topics of physics get in touch with our mentors here at byjus.com.
Visit our website to find more on JEE syllabus, JEE Preparation tips, Important books for JEE.
Comments