Applications Of Integration And Differentiation | Distance,Velocity,Acceleration

Here students will learn about the various applications of integration along with few suitable examples.

Integration

Let us imagine a situation where the acceleration of a vehicle changes with time. In such a situation, it is very tough to determine the instantaneous velocity of the vehicle through primitive formulas as the acceleration is not constant. If we plot the velocity-time graph for such vehicle, we notice that the plot is not a straight line which stands for the case that rate of change in velocity is not the same at all instants. We know that slope at any point on the curve is the ratio of the difference of y-coordinates to the x- coordinates. In a velocity-time graph, acceleration, ‘a’ for a small change in velocity, dv with time dt can be given as:

\(\begin{array}{l}a = \frac{dv}{dt}\end{array} \)

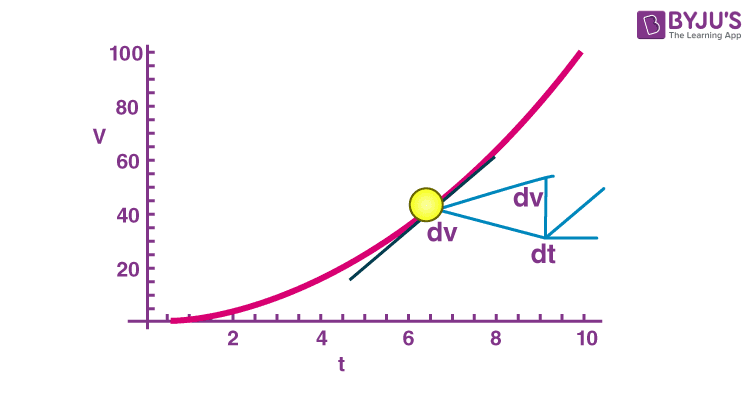
Application of integrals

Thus, instantaneous acceleration can be seen as the slope of the tangent drawn to the v-t curve at any instant. From the equation we also observe the integral formula,

a dt = dv

\(\begin{array}{l}\int_{0}^{t}a\ dt =\int_{0}^{v} dv\end{array} \)

For linear dependence of acceleration on time, a graph is plotted below:

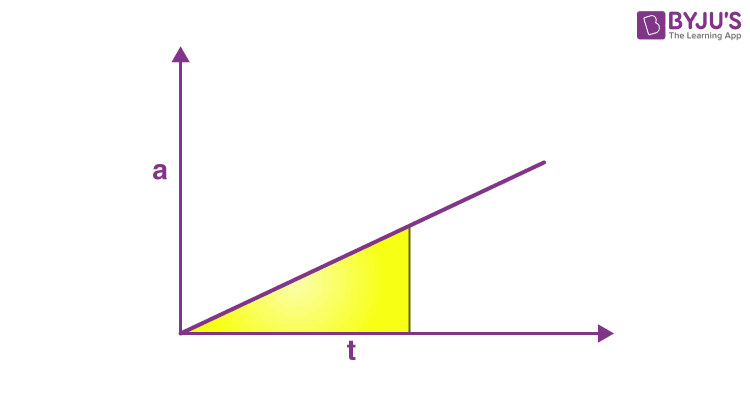
Acceleration Time graph

Hence, we can also conclude that the area of acceleration time graph at any instant gives us the velocity at that instant. Therefore, the velocity at any instant can be determined by integration of the acceleration time curve. Some common applications of integration and integral formulas are:

Determination of the total growth in an area at any time, if the growth function is given with respect to time.

Calculation Of Area Bounded By Curves

Illustration 1: An object starting from rest travels for 10 seconds. Calculate the distance travelled in 5 seconds, if the velocity as a function of time is given as:

\(\begin{array}{l}V = 2t^2 ~–~ t\end{array} \)

Solution: Let the distance travelled in 10 seconds be x meters. General equation for velocity for a given distance dx covered in time dt can be given as:

v = dx/dt
or v dt = dx

Integrating both sides, from time t = 0 to t = 5 seconds, we obtain,

\(\begin{array}{l}\int_{0}^{5}(2t^2~ –~ t)dt=\int_{0}^{x}~dx\end{array} \)

\(\begin{array}{l}\int_{0}^{5}~(2t^2)dt~-~ \int_{0}^{5}(t)dt=\int_{0}^{x}~dx\end{array} \)

\(\begin{array}{l} |\frac{2t^3}{3} – \frac{t^2}{2}|_0^5 = [x]_0^5\end{array} \)

or x = 4256 meters

Area bounded by curves:

We have studied different ways of calculating area covered by triangle, rectangle, etc. in geometry. It becomes very hard for us to devise general formulas for complex curves using geometry. Hence, for calculating area bounded by these curves, we generally go for integration within the limits of the curve. Such method of integration is better known as definite integration.

Illustration 2: Find the area bounded by the curve y = cos x between x = 0 and x = π.
Solution:

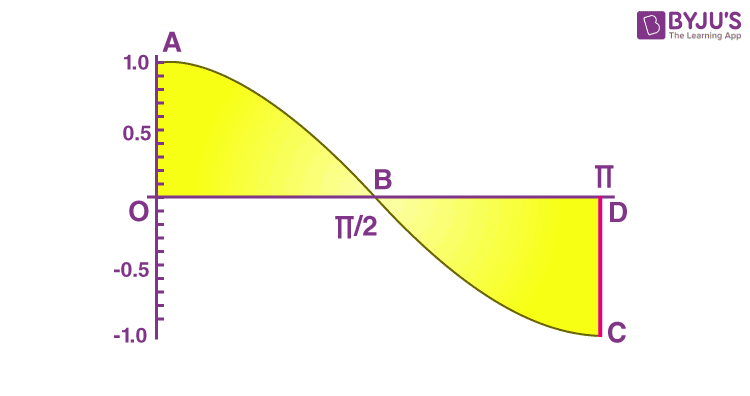
Application of Integration

Required area = area of the figure OABO + area of the figure BCDB

\(\begin{array}{l}\int_{0}^{\frac{\pi}{2}}cos(x)~ dx +|\int_{\frac{\pi}{2}}^{\pi}cos(x) ~dx|\end{array} \)

\(\begin{array}{l}= [sin(\frac{\pi}{2}) – sin(0)] + |[sin(\pi) – sin(\frac{\pi}{2})]|\end{array} \)

= 1 + 1

=2

Application of Integration – Area Under the Curve

Applications of Integrals – JEE Important and Previous Year Questions

For detailed discussion on applications of integration, download BYJU’S – the learning app. To know more about JEE syllabus, JEE preparation tips, JEE books, JEE Revision tips, JEE Study techniques, etc., visit our website www.byjus.com.

Application of Integrals – Top 10 Must-Do JEE Main Important Questions

Comments

Leave a Comment Cancel reply