JEE Main 2021 February 25 – Shift 2 Physics Question Paper with Solutions

SECTION A

Question 1: Match List I with List II.

Choose the correct answer form the options given below:

a. (a)-(ii), (b)- (i), (c)-(iv), (d)-(iii)
b. (a)-(ii), (b)- (iv), (c)-(i), (d)-(iii)
c. (a)-(ii), (b)- (i), (c)-(iii), (d)-(iv)
d. (a)-(iii), (b)- (iv), (c)-(i), (d)-(ii)

Answer: (b)

(a) Rectifier:- used to convert A.C voltage into D.C. Voltage.

(b) Stabilizer:- used for constant output voltage even when the input voltage or load current change

(c) Transformer:- used either for stepping up or stepping down the A.C. voltage.

(d) Filter:- used to remove any ripple in the rectified output voltage.

Question 2: Y = A sin(ωt + ϕ₀) is the time – displacement equation of an SHM, At t = 0, the displacement of the particle is Y = A/2 and it is moving along negative x-direction. Then, the initial phase angle ϕ₀ will be.

a. π/6
b. π/3
c. 2π/3
d. 5π/6

Answer: (d)

y = A sin (ωt + ϕ)

t = 0, x = A/2

1/2 = sin ϕ

ϕ = π/6, 5π/6

v = dy/dt = A ωcos(ωt + ϕ)

t = 0, v = A ωcosϕ

ϕ = π/6, for v (positive)

ϕ = 5π/6, for v (negative)

∴ϕ = 5π/6

Question 3: Two identical springs of spring constant ‘2K’ are attached to a block of mass m and to fixed support (see figure). When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. Then, time period of oscillations of this system is:

a. π√(m/k)
b. π√(m/2k)
c. 2π√(m/k)
d. 2π√(m/2k)

Answer: (a)

Springs are in parallel combination.

Hence, K_eff = 2k + 2k = 4k

∵ T = 2π √(m/k_eff)

 = 2π√(m/4k)

T  = π √(m/k)

Question 4: The wavelength of the photon emitted by a hydrogen atom when an electron makes a transition from n = 2 to n = 1 state is:

a. 194.8 nm
b. 490.7 nm
c. 913.3 nm
d. 121.8 nm

Answer: (d)

∆E = 10.2 eV is the energy difference between the state n = 2 & n = 1

∆E = –3.4 – (–13.6) = 10.2 eV

hc/λ = 10.2 ev

λ = hc/(10.2)e (in meters) where ‘e’ = 1.6 × 10^–19 J/V

= 12400/10.2 Å (because hc = 12400 eV nm)

= 121.56 nm

≃ 121.8 nm

Question 5: In a ferromagnetic material below the Curie temperature, a domain is defined as:

a. a macroscopic region with consecutive magnetic diploes oriented in opposite direction.
b. a macroscopic region with zero magnetization.
c. a macroscopic region with saturation magnetization.
d. a macroscopic region with randomly oriented magnetic dipoles.

Answer: (c)

In a ferromagnetic material below the Curie temperature, domain is defined as a macroscopic region with saturation magnetization.

Question 6: The point A moves with a uniform speed along the circumference of a circle of radius 0.36m and cover 30^o in 0.1s. The perpendicular projection ‘P’ form ‘A’ on the diameter MN represents the simple harmonic motion of ‘P’. The restoring force per unit mass when P touches M will be:

a. 100 N
b. 50 N
c. 9.87 N
d. 0.49 N

Answer: (c)

The point a covers 30^o in 0.1 sec.

Means

π/6 → 0.1sec.

1 → 0.1/(π/6)

2π = → 0.1×6×2π/π

T = 1.2 sec.

We know that ω = 2π/T

ω = 2π/1.2

Restoring force (F) = mω²A

Then, Restoring force per unit mass (F/m) = ω²A

F/m = (2π/1.2)²×0.36

≃ 9.87 N

Question 7: The stopping potential for electrons emitted from a photosensitive surface illuminated by light of wavelength 491 nm is 0.710 V. When the incident wavelength is changed to a new value, the stopping potential is 1.43 V. The new wavelength is:

a. 400 nm
b. 382 nm
c. 309 nm
d. 329 nm

Answer: (b)

From the photoelectric effect equation

hc/λ = ϕ + ev_s

where V_s is the stopping potential and ϕ is work function of the metal.

So, ev_s1 = hc/λ₁ – ϕ ……(i)

ev_s2 = hc/λ₂ – ϕ …..(ii)

Subtract equation (i) from equation (ii)

ev_s1 – ev_s2 = hc/λ₁– hc/λ₂

v_s1 – v_s2 = (hc/e) (1/λ₁ – 1/λ₂)

(0.710 – 1.43) = 1240 (1/491 – 1/λ₂)

(because hc = 1240 eV nm)

-0.72/1240 = 1/491 – 1/λ₂

1/λ₂ = 1/491 + 0.72/1240

1/λ₂ = 0.00203 + 0.00058

1/λ₂ = 0.00261

λ₂ = 383.14

λ₂ ≃ 382 nm

Question 8: A charge ‘q’ is placed at one corner of a cube as shown in figure. The flux of electrostatic field

a. q/48ε₀
b. q/8ε₀
c. q/24ε₀
d. q/4ε₀

Answer: (c)

Total flux through the cube = (q/ε₀)× ⅛ = q/8ε₀

Total flux through one “outer” face of the cube = (q/8ε₀)×1/3 = q/24ε₀

Hence, total flux through shaded area

ϕ_T = (q/24ε₀ + q/24ε₀)×1/2 [half of each face is shaded]

ϕ_T = q/24ε₀

Question 9: A sphere of radius ‘a’ and mass ‘m’ rolls along horizontal plane with constant speed v₀. It encounters an inclined plane at angle θ and climbs upward. Assuming that it rolls without slipping how far up the sphere will travel (along the incline)?

a. (⅖) v₀²/gsin θ
b. 10v₀²/7gsin θ
c. v₀²/5gsin θ
d. 7v₀²/10gsin θ

Answer: (d)

From energy conservation

mgh = ½ mv² + ½ Iω²

mgh = ½ mv² + ½×(⅖)ma²× v₀²/a²

gh = ½ v₀²+ ⅕ v₀²

gh = (7/10)v₀²

h = (7/10)v₀²/g

From triangle, sinθ = h/l

Then, h = lsinθ

l sinθ = (7/10) (v₀²/g)

l = (7/10) (v₀²/gsin θ)

Question 10: Consider the diffraction pattern obtained from the sunlight incident on a pinhole of diameter 0.1 μm. If the diameter of the pinhole is slightly increased, it will affect the diffraction pattern such that:

a. its size decreases, but intensity increases
b. its size increases, but intensity decreases
c. its size increases, and intensity increases
d. its size decreases, and intensity decreases

Answer: (a)

For diffraction through a single slit, for first minimum.

sin θ = 1.22λ/D

If D is increased, then sinθ will decrease i.e θ will decrease

∴ size of circular fringe will decrease but intensity increases.

Question 11: An electron of mass m_e and a proton of mass m_p = 1836 m_e are moving with the same speed. The ratio of their de Broglie wavelength λ_electron/λ_Proton will be:

a. 918
b. 1836
c. 1/1836
d. 1

Answer: (b)

Given mass of electron = m_e

Mass of proton = m_p

∴ given m_p = 1836 m_e

From de-Broglie wavelength

λ = h/p = h/mv

λ_e/λ_p = m_p/m_e [v is same]

= 1836m_e/m_e

λ_e/λ_p= 1836

Question 12: Thermodynamic process is shown below on a P-V diagram for one mole of an ideal gas. If V₂ = 2V₁ then the ratio of temperature T₂/T₁ is:

a. 1/√2
b. 1/2
c. 2
d. √2

Answer: (d)

From P-V diagram,

Given PV^1/2 = constant …..(i)

We know that

PV = nRT

P ∝ (T/V) [for 1 mole]

Put in equation (i)

(T/V) (V)^1/2 = constant

T ∝V^1/2

T₂/T₁ = √(V₂/V₁)

T₂/T₁ = √(2V₁/V₁)

T₂/T₁ = √2

Question 13: A stone is dropped from the top of a building. When it crosses a point 5m below the top, another stone starts to fall from a point 25m below the top, both stones reach the bottom of building simultaneously. The height of the building is: [Take g = 10 m/s²]

a. 45 m
b. 35 m
c. 25 m
d. 50 m

Answer: (a)

Velocity of particle (1) at 5m below top u₁ = √2gh = √(2×10×5) =10 m/s

For particle (1), using 2^nd equation of motion

20+h = 10t + ½ gt² …..(i)

For particle (2), using 2^nd equation of motion

h = ½ gt² …..(ii)

Put equation (ii) in equation (i)

20 + ½ gt² = 10t + ½ gt²

t = 2 sec.

Put in equation (ii)

h = ½ gt²

= ½ ×10 × 2²

h = 20m

The height of the building = 25 + 20 = 45m

Question 14: If a message signal of frequency ‘f_m‘ is amplitude modulated with a carrier signal of frequency ‘f_c‘ and radiated through an antenna, the wavelength of the corresponding signal in air is:

[Given, C is the speed of electromagnetic waves in vacuum/air]

a. c/(f_c+f_m)
b. c/(f_c-f_m)
c. c/f_m
d. c/f_c

Answer: (d)

Equation of amplitude modulated wave y = (A_c + A_m sin ω_mt) sin ω_ct

Here angular frequency of modulated signal = ω_c

Thus frequency of modulated signal = f_c

Thus wavelength = c/f_c

Question 15: Given below are two statements:

Statement I: In a diatomic molecule, the rotational energy at a given temperature obeys Maxwell’s distribution.

Statement II: In a diatomic molecule, the rotational energy at a given temperature equals the translational kinetic energy for each molecule.

In the light of the above statements, choose the correct answer from the options given below:

a. Both statement I and statement II are false.
b. Both statement I and statement II are true.
c. Statement I is false but statement II is true.
d. Statement I is true but statement II is false.

Answer: (d)

The translational kinetic energy & rotational kinetic energy both obey Maxwell’s distribution independent of each other.

T.K.E. of diatomic molecules = (3/2) kT [3 translational D.O.F.]

R.K.E. of diatomic molecules = (2/2) kT = [2 rotational D.O.F.]

So statement I is true but statement II is false.

Question 16: An electron with kinetic energy K₁ enters between parallel plates of a capacitor at an angle ‘α’ with the plates. It leaves the plates at angle ‘β’ with kinetic energy K₂. Then the ratio of kinetic energies K₁ : K₂ will be:

a. sin²β/cos²α
b. cos²β/cos²α
c. cosβ/sinα
d. cosβ/cosα

Answer: (b)

∵v₁cosα = v₂cosβ [electric field inside a parallel plate capacitor is perpendicular to the plates, hence, there will be no change in parallel component of velocity]

v₁/v₂ = cosβ/cosα

Then the ratio of kinetic energies

k₁/k₂ = ½ mv₁²/ ½ mv₂² = (v₁/v₂)² = (cosβ/cosα)²

k₁/k₂ = cos²β/cos²α

Question 17: An LCR circuit contains resistance of 110 Ω and a supply of 220 V at 300 rad/s angular frequency. If only capacitance is removed from the circuit, current lags behind the voltage by 45⁰. If on the other hand, only inductor is removed the current leads by 45⁰ with the applied voltage. The rms current flowing in the circuit will be:

a. 2.5 A
b. 2 A
c. 1 A
d. 1.5 A

Answer: (b)

When L and C are connected with R in series the circuit will come in resonance So, current in the circuit will be:

I_rms = V_rms/R

= 220/110

= 2 A

Question 18: For extrinsic semiconductors: when doping level is increased;

a. Fermi–level of p and n-type semiconductors will not be affected.
b. Fermi–level of p-type semiconductors will go downward and Fermi–level of n-type semiconductor will go upward.
c. Fermi–level of both p–type and n–type semiconductors will go upward for T >T_FK and downward for T<T_FK, where T_F is Fermi temperature.
d. Fermi–level of p-type semiconductor will go upward and Fermi–level of n–type semiconductors will go downward.

Answer: (b)

In n-type semiconductor, pentavalent impurity is added. Each pentavalent impurity donates a free electron. So the Fermi-level of n-type semiconductor will go upward and in p-type semiconductor, trivalent impurity is added. Each trivalent impurity creates a hole in the valence band. So the Fermi-level of p-type semiconductor will go downward.

Question 19: The truth table for the following logic circuit is:

Answer: (4)

If A = B = 0 then output y = 1

If A = B = 1 then output y = 1

Question 20: If e is the electronic charged, c is the speed of light in free space and h is planck’s constant, the quantity (1/4πε₀) |e|²/hc has dimensions of:

a.[ LC^-1]
b. [M⁰ L⁰ T⁰]
c. [ M L T⁰]
d. [M L T^-1]

Answer: (b)

Given

e = electronic charge

c = speed of light in free space

h = planck’s constant

(1/4πε₀) e²/hc = (ke²/hc)× λ²/λ² [multiply and divide by lambda = wavelength]

= F×λ/E [ke²/λ² has dimensions of force and hc/λ = E]

= E/E [F× λ has dimension of E]

= dimensionless

= [ M⁰ L⁰ T⁰]

Section B

Question 1: The percentage increase in the speed of transverse waves produced in a stretched string if the tension is increased by 4% will be ___%.

Answer: 2

Speed of transverse wave is

V = √(T/μ)

Taking log on both sides

ln v = ½ lnT – ½ ln μ

Δv/v = ½ ΔT/T ⇒ (Δv/v)×100 = 1/2 ( ΔT/T)×100

= ½ ×4 [ μ is constant for a string]

(Δv/v)×100 = 2%

Question 2: Two small spheres each of mass 10 mg are suspended from a point by threads 0.5 m long. They are equally charged and repel each other to a distance of 0.20 m. Then charge on each of the sphere is (a/21)×10^-8C. The value of ‘a’ will be________. [Take g = 10 m/s²]

Answer: 20

From FBD, T sinθ = kq²/d² and T cosθ = mg

Dividing them,

mg tanθ = kq²/d²

q = √(mg tanθ)/25k

= √(10×10^-6×10×1/√24(25)9×10⁹)

= √(10^-4×4/√24×25×4×9×10⁹)

= (⅔)√(10^-4/√24×10¹¹)

Thus (a/21)×10^-8 = ⅔ √(10^-15/√24)

= ⅔ √(10^-16/0.49)

a = 2×21/3×0.7

= 20

Question 3: The peak electric field produced by the radiation coming from the 8 W bulb at a distance of 10 m is (x/10) √(µ₀c/π) V/m. The efficiency of the bulb is 10% and it is a point source. The value of x is ___.

Answer: 2

Intensity I = ½ c∈₀E₀²

Intensity = Power / Area = 8 /(4π × 10²)

(8/4π×10²) ×½ =¼ × c ×(1/µ₀c²) ×E₀² [Multiply by ½ and ∈₀ =1/μ₀c²]

E₀ = (2/10)√(µ₀c/π)

⇒ x = 2

Question 4: Two identical conducting spheres with negligible volume have 2.1nC and -0.1nC charges, respectively. They are brought into contact and then separated by a distance of 0.5 m. The electrostatic force acting between the spheres is _______× 10^-9 N. [Given : 4πε₀ = 1/9×10⁹ SI unit]

Answer: 36

When they are brought into contact & then separated by a distance = 0.5 m. Then charge distribution will be

The electrostatic force acting b/w the sphere is

F_e = kq₁q₂/r²

= 9×10⁹×1×10^-9×1×10^-9/(0.5)²

= (900/25) × 10^-9

F_e = 36 ×10^-9 N

Question 5: The initial velocity v₁ required to project a body vertically upward from the surface of the earth to just reach a height of 10R, where R is the radius of the earth, may be described in terms of escape velocity ve such that v_i = √(x/y) v_e. The value of x will be_______.

Answer: 20

Here R = radius of the earth

From energy conservation

-Gm_em/R + ½ mv_i² = -Gm_em/11R + 0

½ mv_i² = (10/11)Gm_em/R

v_i = √(20Gm_e/11R)

v_i = √(20/11)v_e {∵escape  velocity  v_e = √(Gm_e/R)}

Then the value of x = 20

Question 6: A current of 6A enters one corner P of an equilateral triangle PQR having 3 wires of resistance 21Ω each and leaves by the corner R. The currents i₁ in ampere is______.

Answer: 2

The current i₁ = (R₂/(R₁ + R₂))i

= (2/(4+2))×6

i₁ = 2A

Question 7: The wavelength of an X-ray beam is 10 Å. The mass of a fictitious particle having the same energy as that of the X-ray photons is (x/3) h kg. The value of x is _______.

Answer: 10

Given wavelength of an X-ray beam = 10 Å

∵E = hc/λ = mc²

m = hc/λ will be the mass of a particle having the same energy

The mass of a fictitious particle having the same energy as that of the X-ray photons = (x/3)h kg

(x/3) h = h/cλ

x = 3/cλ

= 3/3×10⁸×10×10^-10

x = 10

Question 8: A reversible heat engine converts one- fourth of the heat input into work. When the temperature of the sink is reduced by 52 K, its efficiency is doubled. The temperature in Kelvin of the source will be_______.

Answer: 208

∵ n = W/Q_in = 1/4

¼ = 1 – T₂/T₁ [for reversible heat engine]

T₂/T₁ = 3/4

When the temperature of the sink is reduced by 52k then its efficiency is doubled.

1/2 = 1 -(T₂ – 52)/T₁

(T₂– 52)/T₁ = 1/2

T₂/T₁ – 52/T₁ = 1/2

¾ – 52/T₁ = 1/2

52/T₁ = 1/4

T₁ = 208 K is the source temperature.

Question 9: Two particles having masses 4g and 16g respectively are moving with equal kinetic energies. The ratio of the magnitudes of their linear momentum is n:2. The value of n will be_____.

Answer: 1

Relation b/w kinetic energy & momentum is

p = √(2mKE) (∵KE = same)

p₁/p₂ = √(m₁/m₂)

n/2 = √(4/16)

n = 1

Question 10: If

Answer: 180

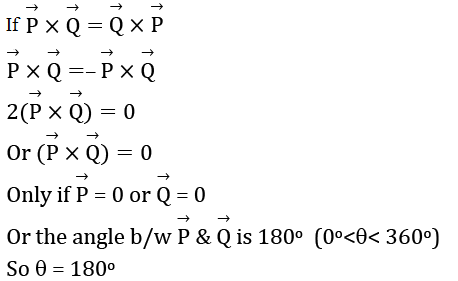
JEE Main 2021 Question Paper Physics Feb 25 Shift 2

Download PDF

carouselExampleControls111

Previous



Next