Measurement Errors

Measurement errors, also called observational errors, are defined as the difference between the actual response acquired and the measured response value. In this case, the actual response value is the average of the infinite number of measurements, while the measured response value is the accurate value.

Classification of Measurement Errors

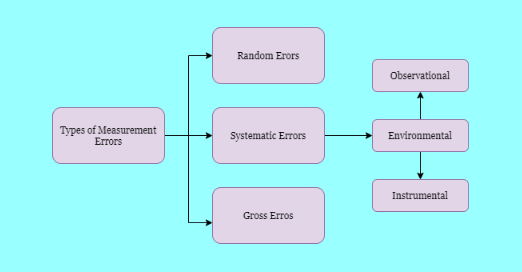
The measurement errors can be classified into three different kinds, and they are

Random Errors

When repeated measurements of value are taken, the inconsistencies in the values account for the so-called random errors. They are always present within the instrument. They occur with fluctuations in the values after each measurement. They can be reduced by taking the average of multiple numbers of measurements.

Systematic Errors

These are not determined by chance but occur due to inaccuracies that are inherent in the system. They are also defined as the error with a non-zero mean, the effect of which is not reduced when the average of the values is taken into consideration. They are sometimes referred to as statistical bias. In general, they are constant and are predictable w.r.t. the true value.

The causes of systematic errors are due to the inappropriate calibration of the instruments or imperfect methods of observation, or the interference of the environment with the measurement process. An example of these errors includes imperfect zeroing of the instrument under study.

Systematic measurement errors are also classified as sampling errors and non-sampling errors.

Sampling Errors: Non-representative sample falls under this category.

Non-Sampling Errors: They include

• Paradigm Error: A scientific approach to the study of the measurable phenomenon.
• Researcher Bias: A researcher is keen to confirm the particular theory which has been devised by them, which then influences the decisions.
• Participant Bias: Participants are influenced by social desirability, supporting or opposing a particular opinion, etc.
• Reliability and validity of measurement tool.

Systematic errors can also be classified into observational errors, instrumental errors and environmental errors.

Gross Error

A gross error arises mainly due to human mistakes, or it can also be said to be a physical error. For instance, a person takes the wrong measurement or reading while using an instrument. Incorrect data is recorded, and this results in a gross error. It can be avoided by being careful and making sure that the reading that is taken is correct. Additionally, two or more readings can be taken of the measurement quantity.

Error Interval

It is the interval that defines the boundary for the actual value to lie on. For example, consider an experiment that gave you the final reading, say 10 A. If the precision is to be taken into account, say some 2%, then it means the actual value lies between (10-0.02) and (10+0.02) è between 9.98 and 10.02.

The estimation of an error interval gives the absolute error associated with the instrument.

Type A and Type B Evaluation of Uncertainty

Type A measurement takes into account that the knowledge of an input quantity is taken only after considering repeated measured values. This process is called type A evaluation of uncertainty. Here, we consider repeated values for measurement in input, or in other words, we consider the Gaussian distribution.

Thus, there is an expectation which is equal to the average of the measured response values. The standard deviation = the average of all the standard deviations. If we evaluate uncertainty, taking into account only a few measured response values, it can be considered as a t-distribution.

On the other hand, type B measurement takes into account scientific judgement or other information concerning the possible values of the quantity. We can term this as a type B evaluation of uncertainty. Here, the information that is available to us is often the value that lies in a specified interval. Here, the concept of a rectangular probability distribution with limits is used.

Statistical Methods of Assessing Measurement Error

There are certain methods that are adopted to assess measurement error, which include

Standard Error of Measurement (SEM): It tells about the deviations or true values of how an instrument, when used multiple times, produces the desired output.

Coefficient of Variation (CV): It is defined as how the values vary on repeated measurements. If the CV is low in value implies the results are closer to the true value.

Limits of Agreement (LOA): It gives the estimate of the interval where a proportion of the differences lie between the measurements.

Ways to Minimise Errors

• Use instruments of higher precision.
• Improve the experimental techniques.
• Adjust the zero of the instruments correctly.
• Take the value of the reading by standing straight to the instrument and not from the sides to avoid parallax errors.
• Repeat the experiment several times and take its algebraic mean for a closer result.
• Take care of the environment, if possible.
• Take the measurements carefully in order to avoid gross errors.

Other Types of Errors

There are various types of errors that can happen in our common day-to-day life. Some of them are

Absolute Error: It is defined as the amount of error in the measurement. For example, we have a sack whose actual weight is said to be 100 kg. Suppose in a weighing machine, the sack weighs out to be 150 kgs, then there is a 50 kg error difference associated with the weighing machine. This associated error of the machine is referred to as an absolute error.

Greatest Possible Error: It is the error which is defined to be one-half of a measuring unit.

Instrument Error: It is the error that is associated with the instrument. This simply tells the inaccuracy of the instrument.

Operator Error: The errors that are caused by the operator is called operating error. For e.g., in an experiment to be conducted in the lab, a man notes the voltmeter to read 5 volts, where it actually was 4 V, then the error caused by the measurement would be due to the man who observed the value. Thus, such type of error is commonly referred to as operator error. They are also called personal errors.

Measurement Location Error: The errors that are caused by the instrument that is kept at a location in which it was not bound to be kept is called a measurement location error. For example, take the case of a thermometer, which is recommended to be kept away from the sun. Suppose the thermometer is placed within the reach of sunlight, and then after the values noted using that particular thermometer, there are chances of the error to occur. Such cumulative errors are broadly classified under this category.

Parallax Error: These errors happen due to wrong sides of measurement being taken. Always take readings by standing straight in front of the instrument and not from its sides.

External Error: The errors that are caused due to external factors like wind, environment, etc., contribute to external errors. 

Percentage Error: The error that is defined as the ratio of the difference between the actual value and the measured value to the actual value is called a percentage error.

Relative Error: It is defined as the ratio of the absolute error to the measured value.

Solved Problems

A resistor is marked in a laboratory with the specifications 100 ohms, 10 %. Find the true value of the resistor.

Answer: The percentage error is given to be 10%. It means the true value is 100+ 10% or 100-10%

i.e., 10% of 100 = 10. Therefore, values = 90 ohms to 110 ohms.