Modulus of Elasticity

Before we understand what the Modulus of Elasticity is, first, we need to know elastic constants. Why do we need elastic constants? What are the types, and where are they all used? So let’s begin.

Elastic Constants

Elastic constants are those constants which determine the deformation produced by a given stress system acting on the material.

• Elastic constants are used to determine engineering strain theoretically.
• They are used to obtain a relationship between engineering stress and engineering strain.
• For a homogeneous and isotropic material, the number of elastic constants is 4.

Types of Elastic Constants

• Young’s modulus or modulus of elasticity (E)
• Shear modulus or modulus of rigidity (G)
• Bulk modulus (K)
• Poisson’s ratio (µ)

In this article, we will discuss only the first type, that is, Young’s modulus or modulus of elasticity (E).

Relationship between Elastic Constants

1. E = 2G (1+ µ)
2. E = 3 K (1-2µ)
3. –E = 9KG / G+3K

Hope you have understood the relation between Young’s modulus and bulk modulus k and the modulus of rigid.

The value of any constant is always greater than or equal to 0. A negative sign only shows the direction.

Definition of Modulus of Elasticity

As per Hooke’s law, up to the proportional limit, “for small deformation, stress is directly proportional to strain.”

Mathematically, Hooke’s Law is expressed as follows:

Stress α Strain

σ = E ε

In the formula mentioned above, “E” is termed as the modulus of elasticity.

σ is the stress, and ε denotes strain.

We can write the expression for the modulus of elasticity using the above equation as,

E = (F*L) / (A * δL)

So, we can define the modulus of elasticity as the ratio of normal stress to longitudinal strain.

Unit of Modulus of Elasticity

The unit of normal stress is Pascal, and longitudinal strain has no unit because it is the ratio of change in length to the original length. So, the unit of modulus of elasticity is the same as of stress, and it is Pascal (Pa). Most commonly, we use Megapascals (MPa) and Gigapascals (GPa) to measure the modulus of elasticity.

1 MPa = Pa

1 GPa = Pa

How to Measure Young’s Modulus or Modulus of Elasticity?

Let us take a rod of a ductile material that is mild steel. Now, do a tension test on the Universal testing machine. After the tension test, when we plot the stress-strain diagram, we get a curve like the one below.

From the curve, we see that from point O to B, the region is an elastic region. After that, the plastic deformation starts. Point A in the curve shows the limit of proportionality. For this curve, we can write the value of the modulus of elasticity (E) is equal to the slope of the stress-strain curve up to A.

If the value of E increases, then longitudinal strain decreases, which means a change in length decreases.

Here are some values of E for the most commonly used materials.

• Mild steel- E = 200 GPa
• Cast iron E = 100 GPa
• Aluminium E = 200/3 GPa

Determination of Young’s Modulus of the Material of a Wire

Make an experimental arrangement, as shown in the figure, to determine the value of Young’s modulus of a material of wire under tension.

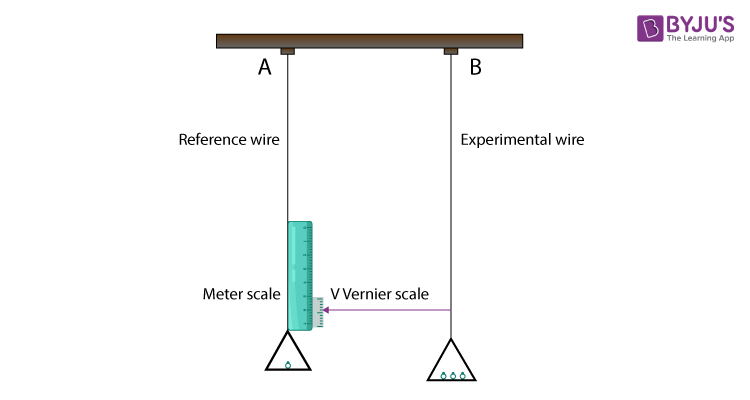
Take two identical straight wires (same length and equal radius), A and B. Now, fix its end from a fixed, rigid support. The wire A is the reference wire, and it carries a millimetre main scale M and a pan to place weight. The wire B is the experimental wire. It also carries a pan in which known weights are placed. At the bottom of the wire, B attaches a vernier scale V.

Now, after putting the weight in the pan connected to B, it exerts a downward force. In the influence of this downward force (tensile stress), wire B gets stretched. This elongation (increase in length) of the wire B is measured by the vernier scale. The reference wire A is used to compensate for any change in length that may occur due to a change in room temperature. Initially, give a small load to both wires A and B so that both be straight and take the Vernier reading. Now, increase the load gradually in wire B and note down the vernier reading. The difference between these two vernier readings gives the change in length produced in the wire.

Let the initial radius and length of wire B be r and L, respectively,

Then, the cross-sectional area of the wire would be pr²

Let M be the mass that is responsible for an elongation DL in the wire B.

Then, the applied force is equal to Mg, where g is the acceleration due to gravity.

From the equation,

E= (F/A) / (DL/L)

= (F × L) / (A × DL)

The Young’s modulus of the material of the experimental wire B is given by,

Y = σ/ε

Y = (F/A)/(ΔL/L)

Y= (F × L) /(A × ΔL)

Y= (Mg × L) /(A × ΔL)

Interesting Facts about the Modulus of Elasticity

• Both the Modulus of Elasticity and Young’s Modulus are the same. The modulus of elasticity is constant.
• Robert Hooke introduces it. Robert Hooke (1635 – 1703) was the early scientist who worked on Applied Mechanics.
• Whereas Young’s modulus was denoted as “E” in 1807 by Thomas Young. It is explained in “Course of Lectures on Natural Philosophy and the Mechanical Arts”, which was written by Thomas Young. He did detailed research on Elasticity Characterisation.
• According to Robert Hook, the value of E depends on both the geometry and material under consideration. To find out the value of E, physical testing is required for any new component.
• Thomas Young said that the value of E depends only on the material, not its geometry”. Thus, he made a revolution in engineering strategies.
• A small piece of rubber and a large piece of rubber has the same elastic modulus.
• The modulus of elasticity is also known as the tensile modulus or elastic modulus.
• It is a fundamental property of every material that cannot be changed. However, it depends upon temperature and pressure.
• The Elastic Modulus is the measure of the stiffness of a material. In other words, it is a measure of how easily any material can be bent or stretched.
• It is the slope of the stress and strain diagram up to the limit of proportionality.

What Are Its Applications? 

• It is used in engineering as well as medical science.
• You can use the elastic modulus to calculate how much a material will stretch and also how much potential energy will be stored.
• The elastic modulus allows you to determine how a given material will respond to stress.
• Elastic modulus is used to characterise biological materials like cartilage and bone as well.

Recommended Videos

Applying Concepts – Hooke’s Law

Stress-Strain Curve – Hooke’s Law