Moment Of Inertia Of A Hollow Sphere

The moment of inertia of a hollow sphere or a spherical shell is often determined by the following formula;

I = MR²

We will look at a simple problem to further understand the usage of the formula.

Let us calculate the moment of inertia of a hollow sphere having a mass of 55.0 kg and a radius of 0.120 m.

Now, to solve such problem we need to use the right formula which is;

I = (2/3)MR²

We will substitute the values,

I =(2/3) (55.0 kg)(0.120 m)²

I = (55.0 kg)(0.0144 m²)

I =(2/3) (0.792 kg.m²)

The moment of inertia of the hollow sphere is 0.528 kg.m².

Hollow Sphere Formula Derivation

We will now understand the derivation of the moment of inertia formula for a hollow sphere.

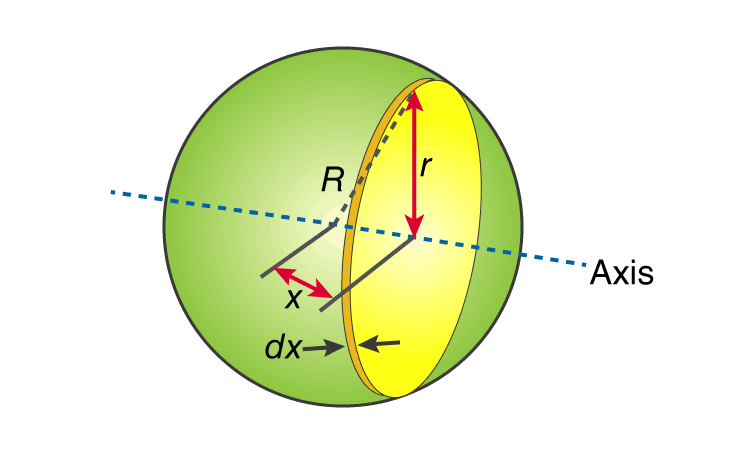
• First, let us consider or recall the moment of inertia of a circle which is

I = mr²

If we apply differential analysis we get;

dl = r² dm

• We have to find the dm,

dm = (M/A) dA

Here, A is the total surface area of the shell = 4πR² (Total surface area of the shell)

dA is the area of the ring formed by differentiation and is expressed as;

dA = R dθ × 2πr

2πr is the circumference of the ring

R dθ is the thickness of the circular ring

Note: We get R dθ from the equation of arc length which is S = R θ

• The next step involves relating r with θ.

If we look at the diagram that is given above, we will see that a right angle triangle with angle θ is present.

We get,

sin θ =  r /R

r = R sin θ

Now dA becomes:

dA = Rdθ × 2πRsinθ

dA = 2πR²sinθ dθ

If we substitute the equation for dA into dm, we get:

dm = (M/A) dA

dm = (M/4πR²)2πR²sinθ dθ

dm = (M/2)sin²θ dθ

We will now substitute the equation given above and for r into the equation for dI. We will get;

dI = r²(M/2)sin²θ dθ

= (Rsinθ)²(M/2)sin²θ dθ

= (MR²/2)sin³θ dθ

Now, we need to split the sin³θ into two, as it depicts the case of integral of odd powered trigonometrical functions. We get;

dI =(MR²/2) sin² θ sin θ dθ

However, sin² θ is normally given as sin² θ = 1- cos² θ. Now,

dI = (MR²/2) (1- cos² θ) sin θ dθ

Integrating within the limits of 0 to π radians. From one end to another.

After this, we use substitution where u = cos θ.

I =(MR²/2) {[ u³/3]₁^-1 – [u]₁^-1

I =(MR²/2) {(1/3)[ (-1)³ -1³] – [-1-1]}

I = (MR²/2){[-1-1]/3 – [-2]}

I =(MR²/2) { [(-2/3) +2]}

I = (MR²/2) x (4/3)

I = (2/3) MR²

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of A Disc
• Moment Of Inertia Of An Annular Disc
• Moment Of Inertia Of A Sphere
• Moment Of Inertia Of Triangle
• Moment Of Inertia Of Rod