Before we learn how to calculate the moment of inertia we will briefly understand what the term means and its definition. Moment of inertia which is also commonly known as rotational inertia or angular mass is a quantity that is used in measuring the amount of torque that is required by a rotating body for creating an angular acceleration in a specific axis. In simple terms, it is a numerical value that can be calculated for rigid bodies that are rotating around a fixed axis.
MOI applies mainly to rotation instead of the linear motion. It is dependent on the distribution of mass and physical shape of the object. It is also based on the configuration of how the object rotates. Usually, an object rotating in different ways will likely have a non-identical moment of inertia. It is denoted by the letter ‘I’.
Calculating Moment Of Inertia
There are several ways to calculate the moment of inertia of a rotating object. Generally, for uniform objects, the moment of inertia is calculated by taking the square of its distance from the axis of rotation (r2) and the product of its mass. Now, in the case of non-uniform objects, we can calculate the moment of inertia by taking the sum of individual point masses at each different radius. If we keep this thing in mind calculating the moment of inertia can be done for any system.
We follow the given formula:
| I = mir2i |
However, this formula is the most simple method for calculating or determining the moment of inertia of objects or shapes. There are a lot of other elaborate objects and we have to apply different formulas to get the desired result. We further use the calculus method of integration as well.
Formulas For Calculating Moment Of Inertia
Here are some of the popular objects or various shapes for which we can calculate the moment of inertia. Their formulas are also given.

| Shape | Formula |
| Solid Sphere | I = (2/5)mr2 |
| Hollow Sphere | I = (2/3)mr2 |
| Solid Cylinder | I = (1/2)mr2 |
| Hollow Cylinder | I = (1/2)m(r12 + r22) |
| Hollow Thin-walled Cylinder | I = mr2 |
| Rectangular plate: when the axis is perpendicular to the centre of the plate | I = (1/12)M(a2 + b2) |
| Rectangular plate: when the axis is at one edge of the plate | I = (1/3)mr2 |
| Thin rod when the axis is at the centre | I = (1/12)ml2 |
| Thin rod when the axis is at the end of the rod | I = (1/3)ml2 |
Practice Questions
1. A spherical disk having mass M = 8 kg and radius R = 7 m is rotating about the y-axis, as shown in the figure. Calculate its moment of inertia?

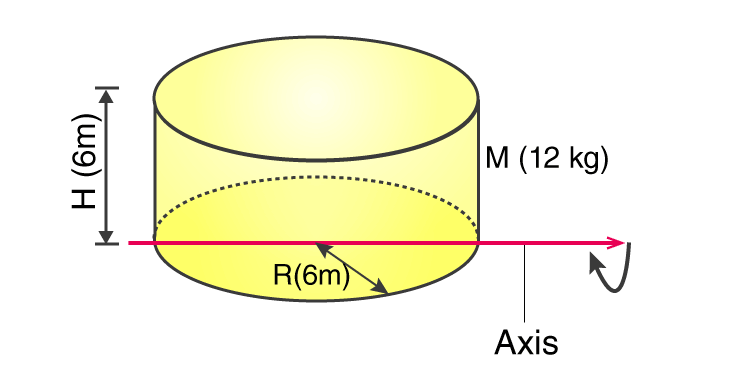
2. There is a solid cylinder of mass 12 kg with homogeneous density having a circular base of radius 6 m and a height of 6 m. Find the moment of inertia if the cylinder rotates about the diameter of the circular base.
3. There is a ring with mass = 3 kg and radius = 4 m which rotates about the y-axis, as shown in the figure below. Calculate its moment of inertia.

Parallel Axis theorem

Frequently Asked Questions on Moment of Inertia
What is the meaning of moment of inertia?
The moment of inertia of a body about a given axis of rotation is defined as the sum of the product of masses of the particles constituting the body and the square of their distance from the axis of rotation.

Comments