How To Find Probability Density Function

Probability theory is the branch of mathematics that deals with probability. A function, whose value at any given sample in the sample space, can be explained as providing a relative likelihood that the value of the random variable would be equal to that sample is called a probability density function. It is denoted as PDF. It is used to represent the probability of the random variable falling within a particular range of values, as opposed to taking on one value.

The probability is given by the integral of this variable’s Probability Density Function over that range, i.e., the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is positive. The integral over the entire space is equal to 1. In this article, we will see how to find the probability density function.

How to Check the Probability Density Function Step by Step

A function f(x) is called a Probability Density Function (P. D. F.) of a continuous random variable x, if it satisfies the criteria

Step 1. f(x) ≥ 0 ∀ x ∈ R. The function f(x) should be greater than or equal to zero.

Step 2.

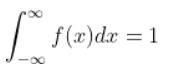
The integral over the function f(x) is equal to 1.

The graphical representation is shown below.

The area under the curve y = f(x) bounded by the X-axis and the coordinates x = a and x = b is equal to 1. It represents the total probability P(a < X < b) which is equal to 1.

Example

Let X be a continuous random variable with the following PDF

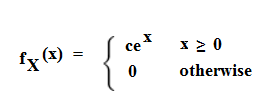
c is a positive constant. Find c, CDF of X, F_X(x), P(1< X < 3)

Solution:

We use the following property.

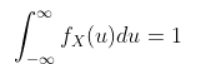
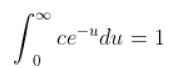
c[-e^-x]₀^∞ = 1

c = 1

To calculate the CDF of X, we use

F_X(x) =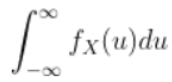

For x < 0, we get F_X(x) = 0. For x ≥ 0, we have F_X(x) =

= 1 – e^-x.

So, F_X(x) = 1 – e^-x for x ≥ 0 and F_X(x) = 0 otherwise.

P(1 < X < 3) =

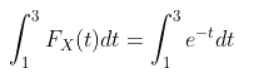
= e^-1 – e^-3

Related Links:

Cumulative Frequency Distribution

Statistics Problems

Probability – Important Topics

Probability – Important Questions