Moment of Inertia of Cone

Moment of inertia of a cone can be expressed using different formulas depending on the structure of the cone. We have to take into account two main types – hollow and solid cones.

Solid Cone

For a solid cone the moment of inertia is found by using the given formula;

I = 3MR² / 10 

Hollow Cone

For a hollow cone, we determine the moment of inertia using;

I = MR² / 2

Students can further check out the full derivation of the formulas from the given links:

Moment of Inertia of Solid Cone Derivation

Here we will look at the derivation as well as the calculation for finding the moment of inertia of a uniform right circular cone about an axis.

We will divide the cone into a small elemental disc where we consider the cone’s radius to be r at a distance x from the top and of thickness dx. We will need to find the mass of the disc and it is given as;

Using the value of r in equa (1)

Now, let us find the moment of inertia of the elemental disc

dI = (1/2) dmr²

I = 3MR² / 10

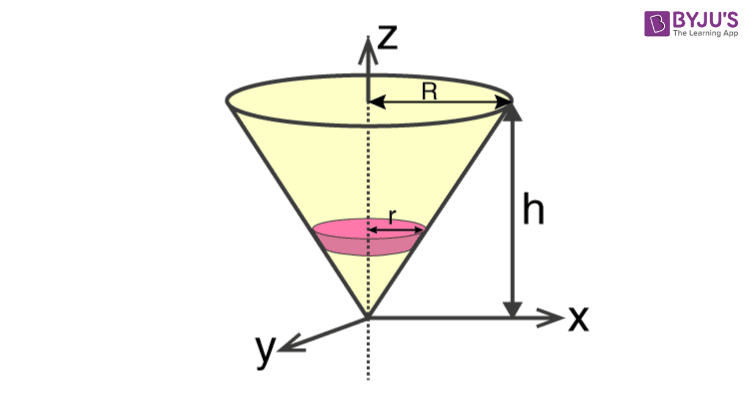
So if we consider the z-axis then we get;

I_Z = 3MR² / 10 

For x-axis;

I_x = I_y = 3m (r² / 4 + h²) / 5 

We will look at one of the simple problems below.

Solved Example To Find Moment Of Inertia Of A Solid Cone

Calculate the moment of inertia of the right circular cone with regards to the x and y-axis. Given, M = 20, R= 4, Height = 2 m.

Solution:

We will solve the problem by using the right formulas.

For the z-axis;

I_z = 3 MR²/ 10

Substituting the values;

I_z = 3 x 20 x 4 x 4/ 10

I_z = 96 kg m²

For the x-axis;

I_x = I_y = 3 m [(r² / 4) + H²]/ 5

I_x = I_y = 3 x 20 x [( 4² / 4) + 2²)] / 5

I_x = 3 x 20 x [( 16 / 4) + 4)]/ 5

I_x = 3 x 20 x 8/5

I_x = 96 kg m²

Parallel Axis Theorem

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of A Disc
• Moment Of Inertia Of An Annular Disc
• Moment Of Inertia Of A Sphere
• Moment Of Inertia Of Triangle
• Moment Of Inertia Of Rod