What Is Quadratic Equation?
Quadratic equations are the polynomial equations of degree 2 in one variable of type f(x) = ax2 + bx + c = 0 where a, b, c, ∈ R and a ≠ 0. It is the general form of a quadratic equation where ‘a’ is called the leading coefficient and ‘c’ is called the absolute term of f (x). The values of x satisfying the quadratic equation are the roots of the quadratic equation (α, β).
Download Complete Chapter Notes of Quadratic Equations
Download Now
The quadratic equation will always have two roots. The nature of roots may be either real or imaginary.
Table of Contents
Quadratic Equation Definition
A quadratic polynomial, when equated to zero, becomes a quadratic equation. In other terms, a quadratic equation is a second degree algebraic equation. The values of x satisfying the equation are called the roots of the quadratic equation.
General from: ax2 + bx + c = 0
Here, a, b, c, ∈ R and a ≠ 0
Examples: 3x2 + x + 5 = 0, -x2 + 7x + 5 = 0, x2 + x = 0.
Quadratic Equations – JEE Flash Lesson

Quadratic Equation Formula
The solution or roots of a quadratic equation are given by the quadratic formula:
x = (α, β) = [-b ± √(b2 – 4ac)]/2a
Formulas for Solving Quadratic Equations
1. The roots of the quadratic equation: x = (-b ± √D)/2a, where D = b2 – 4ac
2. Nature of roots:
- D > 0, roots are real and distinct (unequal)
- D = 0, roots are real and equal (coincident)
- D < 0, roots are imaginary and unequal
3. The roots (α + iβ), (α – iβ) are the conjugate pair of each other.
4. Sum and product of roots: If α and β are the roots of a quadratic equation, then
- S = α+β= -b/a = -coefficient of x/coefficient of x2
- P = αβ = c/a = constant term/coefficient of x2
5. Quadratic equation in the form of roots: x2 – (α + β)x + (αβ) = 0
6. The quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0 have;
- One common root if (b1c2 – b2c1)/(c1a2 – c2a1) = (c1a2 – c2a1)/(a1b2 – a2b1)
- Both roots common if a1/a2 = b1/b2 = c1/c2
7. In quadratic equation ax2 + bx + c = 0 or [(x + b/2a)2 – D/4a2] = 0
- If a > 0, minimum value = 4ac – b2/4a at x = -b/2a.
- If a < 0, maximum value 4ac – b2/4a at x= -b/2a.
8. If α, β, γ are roots of cubic equation ax3 + bx2 + cx + d = 0, then α + β + γ = -b/a, αβ + βγ + λα = c/a, and αβγ = -d/a
9. A quadratic equation becomes an identity (a, b, c = 0) if the equation is satisfied by more than two numbers, i.e. having more than two roots or solutions either real or complex.
⇒ Topics Related to Quadratic Equations:
Roots of Quadratic Equation
The values of variables satisfying the given quadratic equation are called their roots. In other words, x = α is a root of the quadratic equation f(x), if f(α) = 0.
The real roots of equation f(x) = 0 are the x-coordinates of the points where the curve y = f(x) intersects the x-axis.
- One of the roots of the quadratic equation is zero, and the other is -b/a if c = 0
- Both the roots are zero if b = c = 0
- The roots are reciprocal to each other if a = c
What Is Discriminant?
The term (b2 – 4ac) in the quadratic formula is known as the discriminant of a quadratic equation. The discriminant of a quadratic equation reveals the nature of roots.
Nature of Roots of Quadratic Equation
| If the value of discriminant = 0, i.e. b2 – 4ac = 0 | The quadratic equation will have equal roots, i.e., α = β = -b/2a |
| If the value of discriminant < 0, i.e. b2 – 4ac < 0 | The quadratic equation will have imaginary roots, i.e., α = (p + iq) and β = (p – iq), where ‘iq’ is the imaginary part of a complex number |
| If the value of discriminant (D) > 0, i.e. b2 – 4ac > 0 | The quadratic equation will have real roots |
| If the value of discriminant > 0 and D is a perfect square | The quadratic equation will have rational roots |
| If the value of discriminant (D) > 0 and D is not a perfect square | The quadratic equation will have irrational roots, i.e. α = (p + √q) and β=(p – √q) |
| If the value of discriminant > 0, D is a perfect square, a = 1 and b and c are integers | The quadratic equation will have integral roots |
Nature of Roots – Video Lesson

How to Determine the Nature of the Roots of a Quadratic Equation?
Example 1: Find the values of k for which the quadratic expression (x – k) (x – 10) + 1 = 0 has integral roots.
Solution:
The given equation can be rewritten as, x2 – (10 + k)x + 1 + 10k = 0.
D = b2 – 4ac = 100 + k2 + 20k – 40k = k2 – 20k + 96 = (k – 10)2 – 4
The quadratic equation will have integral roots if the value of discriminant > 0, D is a perfect square, a = 1 and b and c are integers.
i.e., (k – 10)2 – D = 4
Since the discriminant is a perfect square, the difference between two perfect squares in R.H.S will be 4 only when D = 0 and (k – 10)2 = 4.
⇒ k – 10 = ± 2. Therefore, the values of k = 8 and 12.
Example 2: Find the values of k such that the equation p/(x + r) + q/(x – r) = k/2x has two equal roots.
Solution:
The given quadratic equation can be rewritten as:
[2p + 2q – k]x2 – 2r[p – q]x + r2k = 0For equal roots, the discriminant (D) = 0, i.e., b2 – 4ac = 0
Here, a = [ 2p + 2q – k ], b = – 2r [ p – q ] and c = r2k
[-2r (p – q)]2 – 4[(2p + 2q – k) (r2k)] = 0r2(p – q)2 – r2k(2p + 2q – k) = 0
Since r ≠ 0, (p – q)2 – k(2p + 2q – k) = 0
k2 – 2(p + q)k + (p – q)2
k = 2(p+q) ± √[4(p + q)2 – 4(p – q)]2/2 = -(p + q) ± √4pq
∴ The values of k = (p + q) ± 2√pq = (√p ± √q)2
Example 3: Find the quadratic equation with rational coefficients when one root is 1/(2 + √5).
Solution:
If the coefficients are rational, then the irrational roots occur in conjugate pairs. Therefore, if one root is α = 1/(2 + √5) = √5 – 2, then the other root will be β = 1/(2 – √5) = -√5 – 2.
The sum of the roots α + β = -4 and the product of roots α β = -1.
Thus, the required equation is x2 + 4x – 1 = 0.
Example 4: Form a quadratic equation with real coefficients when one of its roots is (3 – 2i).
Solution:
Since the complex roots always occur in pairs, the other root is 3 + 2i. Therefore, by obtaining the sum and the product of the roots, we can form the required quadratic equation.
The sum of the roots is
(3 + 2i) + (3 – 2i) = 6. The product of the root is (3 + 2i) × (3 – 2i) = 9 – 4i2 = 9 + 4 = 13.
Hence, the equation is x2 – Sx + P = 0
Therefore, x2 – 6x + 13 = 0 is the required quadratic equation.
Relationship between Coefficient and Roots of Quadratic Equation
If α and β are roots of a Quadratic Equation ax2 + bx + c = 0, then,
- α + β = -b/a
- αβ = c/a
- α – β = ±√[(α + β)2 – 4αβ]
- |α + β| = √D/|a|
The relationship between the roots and coefficient of a polynomial equation can be derived by simplifying the given polynomials and substituting the above results, as shown below.
- α2β + β2α = αβ (α + β) = – bc/a2
- α2 + αβ + β2 = (α + β)2 – αβ = (b2 – ac)/a2
- α2 + β2 = (α – β)2 – 2αβ
- α2 – β2 = (α + β) (α – β)
- α3 + β3 = (α + β)3 – 3αβ(α + β)
- α3 – β3 = (α – β)3 + 3αβ(α – β)
- (α/β)2 + (β/α)2 = α4 + β4/α2β2
Example: If the coefficient of x in the quadratic equation x2 + bx + c =0 was taken as 17 in place of 13, its roots were found to be -2 and -15. Find the roots of the original quadratic equation.
Solution:
Since there is no change in the coefficient of x2 and c, the product of zeroes will remain the same for both equations.
Therefore, the product of zeroes (c) = -2 × -15 = 30,
Since the original value of b is 13,
Sum of zeroes = -b/a = -13.
Hence, the original quadratic equation is:
x2 – (Sum of Zeroes)x + (Product of Zeroes) = 0
x2 + 13x + 30 = 0
∴ (x + 10) (x + 3) = 0
Therefore, the roots of the original quadratic equations are -3 and -10.
Condition for Common Root(s)

Quadratic Equations Having Common Roots
Let β be the common root (solution) of quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0. This implies that a1β2 + b1β + c1 = 0 and a2β2 + b2β + c2 = 0.
Now, solving for β2 and β we will get:
β2/(b1c2 – b2c1) = -β/(a1c2 – a2c1) = 1/(a1b2 – a2b1) [using determinant method]
Therefore, β2 = (b1c2 – b2c1)/ (a1b2 – a2b1) . . . . . . . . . . . . . . . . (1)
And, β = (a2c1 – a1c2)/(a1b2 – a2b1) . . . . . . . . . . . . . . . . (2)
On squaring equation (2) and equating it with equation (1), we get:
(a1b2 – a2b1)/(b1c2 – b2c1) = (a2c1 – a1c2)2
Hence, it is the required condition for quadratic equations having one common root.
If both the roots of quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0 are common then:
a1/a2 = b1/b2 = c1/c2
If α is a repeated root, i.e., the two roots are α, α of equation f(x) = 0, then α will be a root of the derived equation.
f’(x) = 0 where f’(x) = df/dx
If α is a repeated root common in f(x) = 0 and ϕ(x) = 0, then α is a common root both in f’(x) = 0 and ϕ ‘(x) = 0.
How to Solve Quadratic Equations with Common Roots?
Example: For what value of k do both the quadratic equations, 6x2 – 17x + 12 = 0 and 3x2 – 2x + k = 0, will have a common root?
Solution:
If one of the roots of quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0 is common then: (a1b2 – a2b1)(b1c2 – b2c1) = (a2c1 – a1c2)2 . . . . . . . . . . . . . (1)
Form the given quadratic equations, a1 = 6, b1 = -17, c1 = 12, a2 = 3, b2 = -2 and c2 = k.
On substituting these values in equation (1), we will get:
[(6×-2) – (3×-17)] × [-17k – (-2×12)] = (3×12 – 6k)2-663k + 936 = 1296 + 36k2 – 432k
36k2 + 231k + 360 = 0
12k2 + 125k + 120 = 0
(4k + 15) (3k + 8) = 0
Therefore, the values of k are -15/4 and -8/3.
Example: Find the values of k such that the quadratic equations x2 – 11x + k = 0 and x2 – 14x + 2k = 0 have a common factor.
Solution:
Let (x – α) be the common factor of quadratic equations x2 – 11x + k = 0 and x2 – 14x + 2k = 0, then x = α will satisfy the given quadratic equations.
Therefore, α2 – 11α + k = 0 . . . . . . . . . . (1)
And, α2 – 14α + 2k = 0 . . . . . . . . . . . . (2)
On solving Equation (1) and Equation (2), we will get:
α2/(-22k + 14k) = -α/2k – k = 1/(-14 + 11)
Therefore, α2 = (-22k + 14k)/-3 = 8k/3 . . . . . . . (3)
And, α = (2k – k)/(-14 + 11) = k/3 . . . . . . . . . . . (4)
On equating Equation (3) and Equation (4):
8k/3 = (k/3)2
Therefore, the value of k = 24.
Solving Quadratic Equations
There are two methods to solve a quadratic equation
- Algebraic Method
- Graphical Method
Algebraic Method of Solving Quadratic Equations
General Form: ax2 + bx + c = 0;
x2 + bx/a + c/a = 0
⇒ (x + b/2a)2 = b2/4a2 – c/a
Or, (x + b/2a)2 = (b2 – 4ac)/4a2
Or, x + b/2a = ± (√b2 – 4ac)/2a
⇒ x = [-b ± √(b2 – 4ac)]/2a
b2 – 4ac = Discriminant (D)
- α = (-b+√D)/2a
- β = (-b – √D)/2a
α+β= -b/a, α.β = c/a
Therefore, the quadratic equation can be written as,
⇒ x2 – (α + β)x + (α.β) = 0.
Tips to Solve Equations Reducible to Quadratic
- To solve the equations of type ax4 + bx2 + c = 0, put x2 = y
- To solve a.p(x)2 + b.p(x) + c = 0, put p(x) = y.
- To solve a.p(x) + b/p(x) + c = 0, put p(x) = y.
- To solve a(x2 + 1/x2) + b(x + 1/x) + c = 0,put x + 1/x = y and to solve a(x2 + 1/x2) + b(x – 1/x) + c = 0, put x – 1/x = y.
- To solve a reciprocal equation of the type ax4 + bx3 + cx2 + bx + a = 0, a ≠ 0, divide the equation by d2y/dx2 to obtain a(x2 + 1/x2) + b(x + 1/x) + c = 0,and then put x + 1/x = y.
- To solve (x + a) (x + b) (x + c) (x + d) + k = 0 where a + b = c + d, put x2 +(a + b)x = y
- To solve an equation of type √(ax + b) = cx + d or √(ax2 + bx + c) = dx + e, square both sides.
- To solve √(ax + b) ± √(cx + d) = e, transfer one of the radicals to the other side and square both sides. Keep the expression with a radical sign on one side and transfer the remaining expression to the other side.
Graphical Solution of Quadratic Equation
Consider a quadratic equation ax2 + bx + c = 0, where a, b, and c are real and a ≠ 0. The expression can be further rewritten as:
a[(x + b/2a)2 – (D/4a2)] = 0
The above quadratic equation represents a parabola whose vertex is at P [-b/2a, -D/4a] and whose axis is parallel to the y-axis.
In a quadratic equation, the value of ‘a’ determines whether the graph of a quadratic equation will be concave upwards (a > 0) or concave downwards (a < 0). The value of discriminant (b2 – 4ac) determines whether the graph of a quadratic equation will:
- Intersect the x-axis at two points, i.e. b2 – 4ac > 0
- Just touches the x-axis, i.e. b2 – 4ac = 0
- Never intersects the x-axis, i.e. b2 – 4ac < 0
Graphing Quadratic Equations
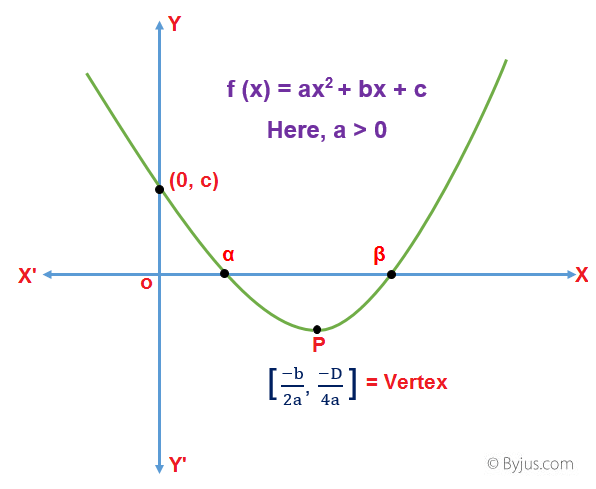
The quadratic equation representing a parabola with vertex at P and axis parallel to the y-axis
Case 1: When a > 0 and b2 – 4ac > 0
The graph of a quadratic equation will be concave upwards and will intersect the x-axis at two points α and β with α < β. The quadratic equation will have two real roots (α and β), and the curve will always lie above the x-axis.
- The quadratic function f(x) will be positive, i.e., f(x) > 0, for the values of x lying in the interval (-∞, α) ∪ (β, ∞)
- The quadratic function f(x) will be equal to zero, i.e., f(x) = 0, if x = α or β
- The quadratic function f(x) will be negative, i.e., f(x) < 0, for the values of x lying in the interval (α, β)
Case 2: When a > 0 and b2 – 4ac = 0
The graph of a quadratic equation will be concave upwards and will touch the x-axis at a point -b/2a. The quadratic equation will have two equal real roots, i.e., α = β. The quadratic function f(x) will be positive, i.e., 0 ≤ f(x), x ∈ R.
Case 3: When a > 0 and b2 – 4ac < 0
The graph of a quadratic equation will be concave upwards and will not intersect the x-axis. The quadratic equation will have imaginary roots, and the curve will always lie above the x-axis. The quadratic function f(x) will be positive, i.e., f(x) > 0, x ∈ R.
Case 4: When a < 0 and b2 – 4ac > 0
The graph of a quadratic equation will be concave downwards and will intersect the x-axis at two points α and β with α < β. The quadratic equation will have two real roots (α and β), and the curve will always lie below the x-axis.
- The quadratic function f(x) will be positive, i.e., f(x) > 0, for the values of x lying in the interval (α, β).
- The quadratic function f(x) will be equal to zero, i.e., f(x) = 0, if x = α or β
- The quadratic function f(x) will be negative, i.e., f(x) < 0 for the values of x lying in the interval (−∞, α) ∪ (β, ∞)
Case 5: When a < 0 and b2 – 4ac = 0
The graph of a quadratic equation will be concave downwards and will touch the x-axis at a point -b/2a. The quadratic equation will have equal real roots, i.e. α = β. The quadratic function f(x) will be negative, i.e. f(x) ≤ 0, x ∈ R.
Case 6: When a < 0 and b2 – 4ac < 0
The graph of a quadratic equation will be concave downwards and will not intersect the x-axis. The quadratic equation will have imaginary roots, and the curve will always lie below the x-axis. The quadratic function f(x) will be negative, i.e. f(x) < 0, x ∈ R.
Location of Roots – Quadratic Equation

Location of Roots – JEE Main and Advanced Questions

Range of Quadratic Equation
Consider a quadratic expression f(x) = ax2 + bx + c, where a ≠ 0 and a, b, and c are real. The quadratic expression can be further rewritten as f(x) = x2 + bax = ca.
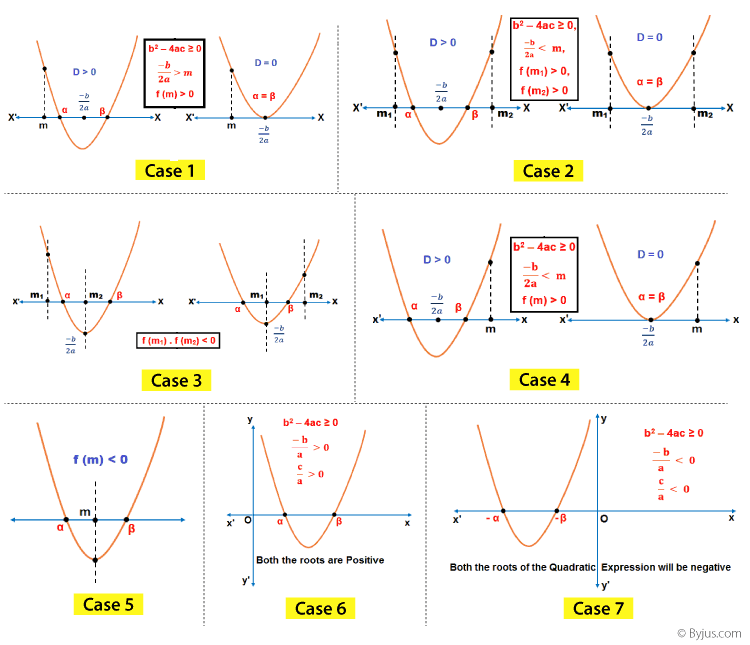
Intervals in which the roots of a Quadratic Equation lie
Case 1: Both the roots of a quadratic equation (α, β) are greater than any given number ‘m’ if,
- b2 – 4ac = (D) ≥ 0,
- -b/2a > m,
- f (m) > 0.
Case 2: Both the roots of a quadratic expression (α, β) are less than any given number ‘m’ if,
- b2 – 4ac = (D) ≥ 0,
- -b/2a < m,
- f(m) > 0.
Case 3: Both the roots of a quadratic expression (α, β) will lie in the given interval (m1, m2) if,
- b2 – 4ac = (D) ≥ 0,
- m1 < -b/2a > m2,
- f(m1) > 0,
- f(m2) > 0.
Case 4: If exactly one root of a quadratic equation (α, β) will lie in the given interval (m1, m2) if, f(m1).f(m2) < 0
Case 5: The given number ‘m’ will lie between the roots of a quadratic equation α and β if f(m) < 0
Case 6: The roots of a quadratic equation α and β will have an opposite sign if f(0) < 0.
Case 7: Both the roots of a quadratic expression α and β are positive if,
- b2 – 4ac = (D) ≥ 0,
- α + β = -b/a > 0,
- αβ = c/a > 0.
Case 8: Both the roots of a quadratic expression α and β are negative if,
- b2 – 4ac = (D) ≥ 0,
- 2. α + β = -b/a < 0,
- 3. αβ = c/a < 0.
How to Find the Range of a Quadratic Equation?
Example 1: Find the range of k for which 6 lies between the roots of the quadratic equation x2 + 2(k – 3)x + 9 = 0.
Solution:
6 will lie between the roots of the quadratic expression f(x) = x2 + 2(k – 3)x + 9 if,
f (6) < 0
i.e. 36 + 2 (k – 3) . 6 + 9 < 0,
36 + 12k – 36 + 9 < 0,
k < -3/4
Therefore, the range of k for which 6 lies between the roots of the given quadratic equation is:
k ∈ (-∞, -3/4)
Example 2: Find the values of k for which exactly one root of the quadratic equation 4x2 – 4(k – 2)x + k – 2 = 0 lies in (0, 1/2).
Solution:
Exactly one root of the quadratic expression 4x2 – 4(k – 2)x + k – 2 = 0 will lie in the given interval if,
f(m1) . f(m2) < 0
i.e., f(0) . f(1/2)<0
Or, (k – 2) [1 – 2 (k – 2) + k – 2] < 0,
Or, (k -2) (3 – k) < 0,
Or, (k – 2) (k – 3) > 0.
Therefore, the values of k for which exactly one root of the given quadratic equation will lie in the interval (0, 1/2):
k ∈ (-∞, 2) ∪ (3, ∞)
Example 3. Find the values of k for which the roots of the quadratic equation x2 – (k – 3)x + k = 0 are greater than 2.
Solution:
The roots of the given quadratic expression f(x) = x2 – (k – 3)x + k are greater than 2 if,
Condition 1: -b/2a > 2
i.e., +(k – 3)/2 >2
Therefore, k > 7 . . . . . . . . . . . . . (1)
Condition 2: f (2) > 0
i.e., 4 – (k – 3)2 + k > 0,
Or, 4 – 2k + 6 + k > 0.
Therefore, k < 10 . . . . . . . . . . . . . . (2)
Condition 3: b2 – 4ac ≥ 0
i.e., (k – 3)2 – 4k ≥ 0,
Or, k2 + 10k + 9 ≥ 0,
Or, (k – 9) (k – 1) ≥ 0.
Therefore, k ∈ (-∞, 1] ∪ [9, ∞) . . . . . . . . . (3)
From equations (1), (2) and (3), the range of ‘k’ for which the roots of the given quadratic expression are greater than 2: k ∈ [9, 10).
Maximum and Minimum Value of Quadratic Equation
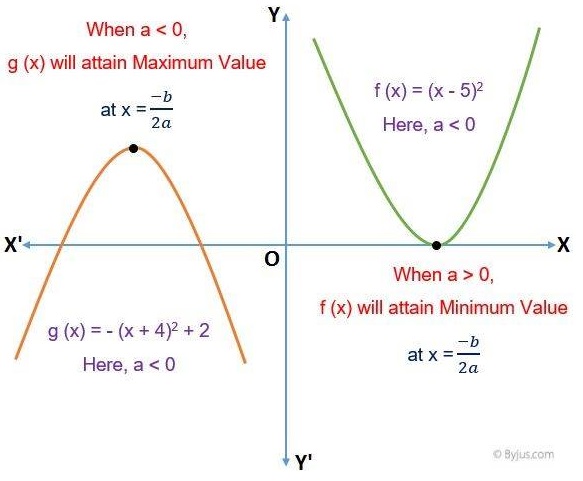
Conditions for Minimum and Maximum Value of Quadratic Equation
To find the minimum value of a quadratic equation, we need to understand the nature of the graph of these equations for different values of ‘a’. The graph of the quadratic equation f(x) = ax2 + bx + c will be either concave upwards (a>0) or concave downwards (a<0), respectively.
When the graph is concave upwards, its vertex determines the minimum value of a quadratic function f(x), and when it is concave downwards, its vertex determines the maximum values of a quadratic function f(x).
How to Find Maximum and Minimum Values of Quadratic Functions?
Case 1: When a > 0, the absolute range of a quadratic equation is given by:
[-b2 – 4ac/4a, ∞) or [-D/4a, ∞)Case 2: When a < 0, the absolute range of a quadratic equation is given by:
(-∞, -D/4a]
Also, the maximum and minimum values of a quadratic equation f(x) occur at x = -b/2a.
If the given quadratic equation is in form f(x) = a(x – h)2 + m, then the value of ‘m’ (vertex) gives us the minimum (when ‘a’ is negative) or maximum (when ‘a’ is positive) values of the given function.
Maximum and Minimum Values in Restricted Domain
Case 1: -b/2a ∉ [m, n]
f(x) = ∈ [ minimum {f(m), f(n)}, maximum {f(m), f(n)} ]
Case 2: -b/2a ∈ [m, n]
f(x) ∈ [minimum {f(m), f(n) – D/4a}, maximum {f(m), f(n), -D/4a}]
Example 1: Find the maximum or minimum value of quadratic expression -4(x – 2)2 + 2.
Solution:
Since the value of ‘a’ is negative, the given quadratic equation will have a maximum value. Hence, the maximum value of the quadratic equation -4(x – 2)2 + 2 is 2.
Example 2: Find the minimum and maximum values of quadratic expression f(x) = x2 – 12x + 11.
Solution:
Since a > 0, the maximum and minimum values of a quadratic expression are given by:
[(-b2 – 4ac)/4a, ∞) or [-D/4a, ∞)Therefore, the minimum value of f(x) is:
-(144 – 44)/4 at x = -(-12/2) = -25 at x = 6.
The maximum value of f(x) is infinity.
Therefore, the range of the given quadratic equation is [- 25, ∞).
Example 3: Find the minimum value of equation y = (2x – 5)/(2x2 + 3x + 6).
Solution:
f(x) will have minimum value at x = -b/2a [Since a>0]
i.e. at x = -3/4.
∴ The minimum value of quadratic equation f(x) = -D/4a = -(9 – 48)/8 = 39/8.
Example 4: Find the range of function f(x) = (x + 2)/(2x2 + 3x + 6), if x is real.
Solution:
Let y = (x + 2)/ (2x2 + 3x + 6)
2x2y + 3xy + 6y = x + 2
2x2y + (3y – 1)x + 6y -2 = x + 2
Now, discriminant = (3y – 1)2 – 4(2y).(6y – 2) ≥ 0 [because x is real]
9y2 + 1 – 6y – 48y2 + 16y ≥ 0
39y2 – 10y – 1 ≤ 0
39y2 – 13y + 3y – 1 ≤ 0
13y(3y – 1) + 1(3y – 1) ≤ 0
∴ The range of quadratic function f(x) = (x+2)/(2x2 + 3x + 6): y ∈ [-1/13, 1/3].
⇒ Try this:
If both the roots of the quadratic equation x2 + x(4 – 2k) + k2 – 3k – 1 = 0 are less than 3, then find the range of values of k.
Ans: k ∈ (-∞, 4).
Descartes’s Rule of Signs for Quadratic Polynomials
This is a very famous rule that helps in getting an idea about the roots of a polynomial equation. The rule states that the number of positive real roots of Pn(x) = 0 cannot be more than the number of sign changes. Similarly, the number of negative roots cannot be more than the number of sign changes in Pn(-x).
Example 1: How many real roots does the equation 2x5 + 2x4 – 11x3 + 9x2 – 4x + 2 = 0 will have?
Solution:
The given equation has 4 sign changes, so it can have a maximum of 4 positive real roots. Now, for f(-x), the equation has only one sign change, i.e. f (-x) = -x5 + 2x4 + x3 + x2 + x + 2 = 0. Hence, the equation will have only one negative real root.
Example 2: How many real roots does the quadratic equation x2 + 3|x| + 2 will have?
Solution:
Since the quadratic equation has no sign change for both f(x) and f(-x), the equation will have no real root.
Sign Convention of Quadratic Equation – ax2 + bx + c = 0
- The roots of a quadratic equation are equal in magnitude but opposite in sign if b = 0 and ac < 0
- The root with greater magnitude is negative if the sign of a = sign of b × sign of c
- If a > 0, c < 0 or a > 0, c > 0; the roots of quadratic equation will have opposite sign
- If y = ax2 + bx + c is positive for all real values of x, a > 0 and D < 0
- If y = ax2 + bx + c is negative for all real values of x, a < 0 and D < 0
Example: For what values of ‘m’ does the quadratic expression x2 + 2(m + 1)x + 9m – 5 = 0 have only negative roots?
Solution:
Here a = 1, b = 2(m + 1), and c = 9m – 5
Therefore, D = 4(m + 1)2 – 4(9m – 5) = 4m2 + 24 – 28m . . . . . (1)
α + β = -2 (m + 1) and αβ = 9m – 5 . . . . . . . . . . . . . . (2)
Now, both the roots of a quadratic expression are negative if b2 – 4ac = (D) ≥ 0, α + β = −ba < 0, and αβ = ca < 0
Therefore, 4m2 + 24 – 28m ≥ 0 [From equation (1)]
i.e., m2 – 7m + 6 ≥ 0
Or, (m – 1) (m – 6) ≥ 0
Therefore, m ≤ 1 or m ≥ 6 . . . . . . . . . . (3)
Now, α + β < 0
i.e., -2(m + 1) < 0 [From equation (2)]
Or, m > -1 . . . . . . . (4)
And, α β < 0
i.e., 9m – 5 < 0
Or, m < 5/9 . . . . . . (5)
From equations (3), (4) and (5), we can conclude that the given quadratic equation will have only negative roots if m ≥ 6.
Quadratic Equations in Two Variables
The general form of a quadratic equation ax2 + 2hxy + by2 + 2gx + 2fy + c can be factorised into two linear factors as shown below,
ax2 + 2(hx + g)x + by2 + 2fy + c = 0 . . . . (i)
Using the quadratic formula in the above equation, we get,
x = [2(hy + g) ± √{4(hy + g)2 – 4a(by2 + 2fy + c)}]/2a
ax + hy + g = ± √(h2y2 + g2 + 2ghy – aby2 – 2afy – ac) . . . . (ii)
At this point, the expression (i) can be resolved into two linear factors if,
(h2 – ab)y2 + 2(gh – af)y + g2 – ac is a perfect square and h2 – ab > 0
But (h2 – ab)y2 + 2(gh – af)y + g2 – ac will be a perfect square if discriminant = 0
i.e. g2h2 + a2f2 – 2afgh – h2g2 + abg2 + ach2 – a2bc = 0 and h2 – ab > 0
abc + 2fgh – af2 – bg2 – ch2 = 0 and h2 – ab > 0
This is the required condition. The condition that this expression may be resolved into two linear rational factors is:
abc + 2fgh – af2 – bg2 – ch2 = 0 and h2 – ab > 0
This expression is called the discriminant of the above quadratic expression.
Biquadratic Equation
A polynomial equation of degree four without the terms of degree three and one is known as a biquadratic equation.
General Form: z4 + a0z2 + c = 0
Examples:
- x4 +16x2 + 6 = 0
- 2x4 + 14x2 + 3 = 0
How to Solve Biquadratic Equations?
Biquadratic equations can be easily solved by converting them into quadratic equations, i.e. by replacing the variable ‘z’ with x2.
Example: Find the zeroes of a biquadratic equation x4 – 3x2 + 2 = 0.
Solution:
Given x4 – 3x2 + 2 = 0
On substituting x2 = z in the given equation, we get,
z2 – 3z + 2 = 0
z2 – 2z – z + 2 = 0
z(z – 2) -1(z – 2) = 0
∴ z = 1 and z = 2
Hence, x = ±√1 and x = ±√2 [Since, z = x²].
Practice Questions for Solving Quadratic Equations
Question 1: If G(x) = px2 + qx + r and H(x) = -px2 + mx + r and p.r ≠ 0, prove that G(x).H(x) = 0 will have exactly two real roots.
Solution:
G(x) will have real roots if q2 – 4pr ≥ 0, and H(x) will have real roots if m2 + 4pr ≥ 0.
Case 1: If pr < 0,
q2 – 4pr ≥ 0, therefore, G(x) will have real root(s).
Case 2: If pr > 0,
m2 + 4pr ≥ 0, therefore, H(x) will also have real root(s).
Hence, at least two roots of G(x).H(x) are real.
Question 2: Find the range in which the value of the given quadratic expression will lie (x2 + 14x + 9)/(x2 + 2x + 3), where x is a real number.
Solution:
Let, y = (x2 + 14x + 9)/(x2 + 2x + 3)
i.e., x2 + 14x + 9 = (x2y + 2xy + 3y)
Or, (1 – y)x2 + (7 – y)2x + 3(3 – y) = 0
Since x is real, b2 – 4ac ≥ 0
i.e. [2(7 – y)]2 – 4[1 – y] × 3[3 – y] ≥ 0
Or, -2y2 – 2y + 40 ≥ 0
Or, (y + 5) (y – 4) ≤ 0
Therefore, the range in which the value of the given quadratic expression will lie is -5 ≤ y ≤ 4.
Question 3: Find the values of x for which the expression (x2 – 4x + 3)/(x2 + x + 1) < 0.
Solution:
Let f(x) = x2 – 4x + 3 and g(x) = x2 + x + 1.
The coefficient of x2 in g(x) is positive, and the value of discriminant (D) < 0. Hence, g(x) is positive for all values of x.
Since, f(x)/g(x) < 0, f (x) must be less than 0.
i.e., x2 – 4x + 3 < 0
Or, (x – 3) (x – 1) < 0
Therefore, 1 < x < 3.
Question 4: Find the values of ‘m’ for which the roots of the given quadratic equation f(x) = 9x2 + (m – 4)x + m/4 satisfy the following given conditions:
- Both the roots of quadratic polynomial f(x) are real and distinct.
- Quadratic expression f(x) has equal roots.
- The roots of the quadratic expression are not real.
- The roots of the quadratic equation have opposite signs.
- Roots are equal in magnitude but have opposite signs.
- Both the roots of the given quadratic equation f(x) are positive.
- Both of the roots are negative.
Solution:
From the given quadratic equation f(x) = 9x2 + (m – 4)/x + m/4,
a = 9, b = (m – 4) and c = m/4
Therefore, D = b2 – 4ac = (m – 4)2 – 4(9).(m/4)
= m2 + 16 – 8m – 9m = m2 – 17m + 16
Therefore, D = m2 – 17m + 16 = (m – 1) (m – 16)
Solution 1. Both the roots of the quadratic equations are real and distinct if,
D = (b2 – 4ac) > 0
i.e., (m – 16) (m – 1) > 0
Note: If ax2 + bx + c > 0, D > 0 and a > 0, then x ∈ (-∞, α) ∪ (β, ∞).
Therefore, both the roots of the given quadratic equation are real and distinct if:
m ∈ (-∞, 1) ∪ (16, ∞).
Solution 2. The quadratic expression f(x) has equal roots if, D = 0
i.e., (m – 16) (m – 1) = 0
Therefore, for m = 16 or m = 1, both the roots of the given quadratic equation are equal.
Solution 3. Roots of the quadratic equation are imaginary if D < 0
i.e., (m – 16) (m – 1) < 0
Note: If ax2 + bx + c > 0, D < 0 and a > 0, then x ∈ R
Therefore, the roots of the given equation are imaginary if m ∈ (1, 16).
Solution 4. Roots of quadratic expression will have an opposite sign if f (0) < 0
Since f(0) = m
Therefore, the roots of the given equation will have an opposite sign if m ∈ (−∞,0).
Solution 5. The roots of quadratic expression are equal in magnitude but opposite sign if,
Condition 1: Sum of roots = 0
i.e., (m – 4)/9 = 0, Therefore, m = 4 . . . . . . . . . . . . . . . (1)
Condition 2: D = (b2 – 4ac) ≥ 0
i.e. (m -1) (m – 16) ≥ 0
Therefore, x ∈ (=∞, 1] ∪ [16, ∞) . . . . . . . . . . . . . . . . (2)
From equation (1) and (2), we conclude that no such value of ‘m’ exist in f(x) when the roots have an opposite sign with equal magnitude.
Solution 6. Both the roots of a given quadratic expression are positive if,
Condition 1: Product of the roots > 0
i.e., m/(4×9) > 0, Therefore, m > 0 . . . . . . . . . . (3)
Condition 2: Sum of the roots > 0
-(m – 4)/9 > 0, Therefore, m < 4 . . . . . . . . . (4)
Condition 3: D = (b2 – 4ac) ≥ 0
From equation (2),
x ∈ (-∞, 1] ∪ [16, ∞) . . . . . . . . (5)
Therefore, from equations (3), (4) and (5), both the roots of f(x) are positive if m ∈ (0,1].
Solution 7. Both the roots are negative if,
Condition 1: The Product of roots > 0
i.e., m/(4×9) > 0, m > 0 . . . . . . . . . . (6)
Condition 2: The Sum of roots < 0
-(m – 4)/9 < 0, m > 4 . . . . . . . . . (7)
Condition 3: D = (b2 – 4ac) ≥ 0
Using equation (2),
x ∈ (-∞, 1] ∪ [16, ∞) . . . . . . . . (8)
Therefore, from equations (6), (7) and (8), both the roots of quadratic expression f (x) are negative if,
m ∈ [16, ∞].
Question 5: The quadratic equations x2 – ax + b = 0 and x2 – px + q = 0 have a common root, and the second equation has equal roots. Show that b + q = ap/2.
Solution:
By considering α and β to be the roots of equation (i) and α to be the common root, we can solve the problem by using the sum and product of the roots formula.
The given quadratic equations are
x2 – ax + b = 0 ………. (i)
x2 – px + q = 0 ………..(ii)
From equation (i), α + β = a, α = b
From equation (ii), 2α = p, α2 = q
b + q = αβ + α2 = α (α + β) = ap/2
Question 6: x2 + ax + bc = 0 and x2 + bx + ca = 0 have a non zero common root and a ≠ b. Show that the other roots are roots of the quadratic equation x2 + cx + ab = 0, c ≠ 0.
Solution:
By considering α to be the common root of the quadratic equations and β, γ to be the other roots of the equations, respectively, then by using the sum and product of roots formula, we can prove this.
Further, α + β = -a and αβ = bc;
α + γ = -b, αγ = ca
2α + β + γ = -(a + b) and α2βγ = abc2 . . . . . . (i)
Therefore, β + γ = c – 2c = -c . . . . . . . (ii)
and, c2βγ = c2ba
Therefore, βγ = ab …. (iii)
From equations (ii) and (iii),
β and γ are the roots of the quadratic equation x2 + cx + ab = 0.
Question 7: The expressions x2 – 11x + a = 0 and x2 – 14x + 2a = 0 must have a common factor and a ≠ 0. Find the common factor and the common root.
Solution:
If (x – α) is the common factor of the given quadratic equations, then x = α becomes the root of the corresponding equation.
Therefore, α2 – 11α + a = 0 and α2 – 14α + 2a = 0
On subtracting the above equations, we get,
3α – a = 0 ⇒ α = a/3
Hence, a2/9 – 11a/3 + a = 0,
On solving the above quadratic equation, we get, a = 0 or 24
Since a ≠ 0, therefore, a = 24.
Question 8: Determine the values of m for which the quadratic equations 3x2 + 4mx + 2 = 0 and 2x2 + 3x – 2 = 0 may have a common root.
Solution:
Consider α to be the common root of the given equations.
Then, 3α2 + 4mα + 2 = 0 and 2α2 + 3α – 2 = 0
Using the cross multiplication method, we have
(-6 – 4)2 = (9 – 8m) (-8m – 6)
⇒ 50 = (8m – 9)(4m + 3)
Or, 32m2 – 12m – 77 = 0
Or, (8m + 11) (4m – 7) = 0
Therefore, the values of m for which the given quadratic equations will have common roots = -11/8 and 7/4.
Question 9: Find the relation between c, a and m if a quadratic equation formed from y2 = 4ax and y = mx + c has equal roots.
Solution:
(mx + c)2 = 4axm2x2 + 2(cm – 2a)x + c2 = 0
Since the roots of this quadratic equation are equal, D = 04(cm – 2a)2 – 4m2c2 = 0
4a2 – 4cma = 0 or a2 = acm
⇒ a = cm or c = a/m.
This is a condition for the line y = mx + c to be tangent to the curve y2 = 4ax.
Question 10: For what values of ‘m’ does the quadratic equation (1 + 2) x2 – 2(1 + 3m)x + (1 + 8m) = 0 have equal roots?
Solution:
The roots are equal if discriminant (D) = 4(1 + 3m)2 – 4(1 + m)(1 + 8m) = 0
Topmost Quadratic Equations Problems for JEE Advanced

Quadratic Equations and Complex Numbers Important JEE Main Questions

Quadratic Equations – Top 12 Most Important and Expected JEE Questions

Quadratic Equations – Rapid Revision Lessons
Nature of Roots

Location of Roots

Also, Practice:-
Previous Year JEE Questions on Quadratic Equations
Quadratic Function Videos
Nature of Graph

Range of Quadratic Function

Quadratic Equations – Lessons for JEE 2023 & 2024
Relation between Roots and Coefficients

Nature of Roots and Common Roots

Range and Graphs of Quadratic Polynomial

Transformation and Location of Roots

Location of Roots and Theory of Equations

Roots and Their Relation with Coefficients

Nature of Roots

Graphical Representation of Quadratic Equations

Transformation of Roots & Location of Roots

Quadratic Equation in Two Variables

Frequently Asked Questions on Quadratic Equation
What are the different ways to solve a quadratic equation?
Solving quadratic equations can be quite difficult sometimes. However, there are several methods that can be used depending on the type of quadratic that needs to be solved. There are mainly four ways of solving a quadratic equation, and they are factoring, using the square roots, completing the square and using the quadratic formula.
What is the standard form of the quadratic equation?
The form ax2 + bx + c = 0 is said to be the standard form of a quadratic equation.
What are the steps involved in factoring a quadratic equation?
The following steps can be used to solve the quadratic equation by the factoring method.
- First, you have to move all terms on one side of the equal sign. Leave zero on the other side and then factor.
- Now, you have to set each factor equal to zero.
- Each equation has to be solved.
- Use the original equation to check the answer.
What is the difference between a quadratic equation and a quadratic expression?
A quadratic equation is said to be any polynomial equation of degree 2 or an equation that is in the form ax2 + bx + c = 0. The quadratic formula, on the other hand, is a formula that is used to solve the quadratic equation. The formula is used to determine the roots/solutions to the equation.
What are the uses of quadratic equations?
Interestingly, quadratic equations are used in our everyday life. It can be used in calculating areas or rooms, determining a product’s profit in business or finding the speed of an object. It is also used in sports and athletics.

Comments