Moment Of Inertia Of Rod

Moment of inertia of a rod whose axis goes through the centre of the rod, having mass (M) and length (L) is generally expressed as;

The moment of inertia can also be expressed using another formula when the axis of the rod goes through the end of the rod. In this case, we use;

Moment Of Inertia Of Rod Formula Derivation / Calculation

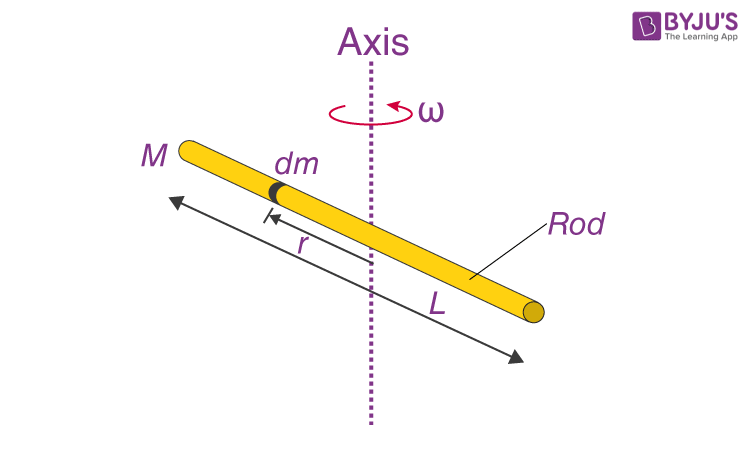
Let us understand the derivation of the moment of inertia for the two moments.

1. When the axis is through the centre of the mass.

We have to keep in mind a few things;

• We have to imagine that the rod is divided into many pieces of infinitesimally thin slices.
• Each slice will have a length of dx and a mass of dm.
• We have to identify the variable to be summed.

In the first instance, the rod must be taken to have an infinite number of point masses. All of their products will be obtained by multiplying the square of the distance from the axis. We also have to consider the exceedingly small element of length dl corresponds to the mass dm. Besides, when we picture or label the origin at the centre of mass that is lying on the line of the axis, we will see that distance of the rod from the left is -L/2, while the distance from the origin to its right is +L/2.

Now,

If we look at the rod we can assume that it is uniform. Therefore the linear density will remain constant and we have;

or = M / L = dm / dl

dm = (M / L) dl

Now we have to replace the value of dm in the expression;

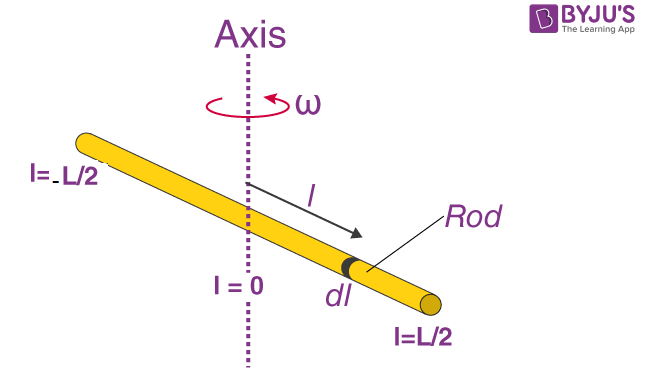
I = _O ∫^M r²dm

I = _-L/2 ∫^L/2 l² (M/L)dl

Here the variable of the integration is the length (dl). The limits have changed from M to the required fraction of L.

I = _-L/2 ∫^L/2 (M/L)l²dl

I = M / L _-L/2^L/2 [l³ / 3]

I = M / 3L [(L / 2)³ – (-L / 2)³]

I = M / 3L [L³ / 8 + L³/ 8³]

I = (M / 3L) . 2L³ / 8

I = (1 / 12) ML²

2. When the axis is through the end of the rod.

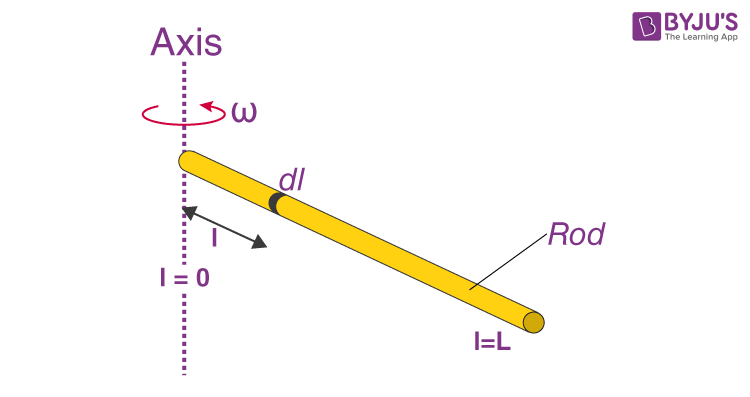
For calculating when the axis is at the end we have to draw the origin at that particular end.

The same expression can be used but with another limit. Since the axis rests at the end, the limit that is used in integration is 0.

I = _O∫^M r²dm

I = _O∫^L l² (M / L) dl

If we apply the integration;

I_end = (M / L )_O∫^L l² dl

I_end = (M / L) ₀^L[l³ / 3]

I_end = (M / 3L) [ L³ – 0³]

I_end = (⅓) ML²

Alternatively, the parallel axis theorem can also be used to determine the expression.

We have;

I = I_cm + Md²

Now if we substitute the values it becomes;

I_end = (1/12) ML² + M (L / 2)²

I_end = (1/12) ML² +( ¼) ML²

I_end = (⅓ )ML²

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of Ellipse
• Moment Of Inertia Of A Cone
• Moment Of Inertia Of Square
• Moment Of Inertia Of Circle
• Moment Of Inertia Of Ring