NERNST Equation

What Is Nernst Equation?

The Nernst equation provides the relation between the cell potential of an electrochemical cell, the standard cell potential, temperature, and the reaction quotient.

Even under non-standard conditions, the cell potentials of electrochemical cells can be determined with the help of the Nernst equation.

The Nernst equation is often used to calculate the cell potential of an electrochemical cell at any given temperature, pressure, and reactant concentration. The equation was introduced by a German chemist, Walther Hermann Nernst.

JEE Main 2021 LIVE Chemistry Paper Solutions 24-Feb Shift-1 Memory-based

Expression of Nernst Equation

The Nernst equation is an equation relating the capacity of an atom/ion to take up one or more electrons (reduction potential) measured at any conditions to that measured at standard conditions (standard reduction potentials) of 298 K and one molar or one atmospheric pressure.

Nernst Equation for Single Electrode Potential

E_cell = E⁰ – [RT/nF] ln Q

Where,

• E_cell = cell potential of the cell
• E⁰ = cell potential under standard conditions
• R = universal gas constant
• T = temperature
• n = number of electrons transferred in the redox reaction
• F = Faraday constant
• Q = reaction quotient

The calculation of single electrode reduction potential (E_red) from the standard single electrode reduction potential (E°_red) for an atom/ion is given by the Nernst equation.

⇒ Also Read: Redox Reactions

For a reduction reaction, the Nernst equation for a single electrode reduction potential for a reduction reaction

Mⁿ⁺ + ne^– → nM is;

E_red = EMⁿ⁺/M = E^oMⁿ⁺/M – [2.303RT/nF] log [1/[Mⁿ⁺]]

Where,

• R is the gas constant = 8.314 J/K Mole
• T = absolute temperature,
• n = number of mole of electron involved,
• F = 96487 (≈96500) coulomb/mole = charge carried by one mole of electrons.
• [Mⁿ⁺] = active mass of the ions. For simplicity, it may be taken as equal to the molar concentration of the salt.

Nernst Equation at 25^oC

For measurements carried out 298 K, the Nernst equation can be expressed as follows:

E = E⁰ – 0.0592/n log₁₀ Q

Therefore, as per the Nernst equation, the overall potential of an electrochemical cell is dependent on the reaction quotient.

Derivation of Nernst Equation

Consider a metal in contact with its own salt-aqueous solution. Reactions of metal losing an electron to become an ion and the ion gaining an electron to return to the atomic state are equally feasible and are in an equilibrium state.

Mⁿ⁺ + ne^– → nM

In the reduction reaction, ‘n’ moles of an electron is taken up by the ion against a reduction potential of E_red.

1. The work done in the movement of electron

W_red = nFE_red

Where,

• F is Faraday = 96487 coulomb = electrical charge carried by one mole of electrons

2. Change in the Gibbs free energy is an indication of spontaneity, and it is also equal to the maximum useful work (other than volume expansion) done in a process.

Combining work done and Gibbs free energy change:

W_red = nFE_red = – ∆G or ∆G = – nFE_red

3. Change in the free energy at standard conditions of 298 K and one molar /one atmospheric pressure conditions is ∆G°. From the above relation, it can be written that

∆G° = – nFE°_red

Where,

• E°_red is the reduction potential measured at standard conditions.

4. During the reaction, concentration keeps changing, and the potential also will decrease with the rate of reaction.

To get the maximum work or maximum free energy change, the concentrations have to be maintained the same. This is possible only by carrying out the reaction under a reversible equilibrium condition.

For a reversible equilibrium reaction, Van’t Hoff isotherm says:

∆G = ∆G° + RT ln K

Where,

• K is the equilibrium constant
• K = Product/Reactant = [M]ⁿ/[M]ⁿ⁺
• R is the Gas constant =8 .314J/K mole
• T is the temperature on the Kelvin scale.

5. Substituting for free energy changes in Van’t Hoff equation,

– nFE_red = – nFE°_red + RT ln [M]/[Mⁿ⁺] = – nFE°_red + 2.303 RT log [M]ⁿ/[Mⁿ⁺]

Dividing both sides by – nF,

or,

The activity of the metal is always considered as equal to unity.

E_red = E°_red – or

This relation connecting reduction potential measurable at conditions other than standard conditions to the standard electrode potential is the Nernst equation.

For reactions conducted at 298 K but different concentrations, the Nernst equation is:

Determining Equilibrium Constant with Nernst Equation

When the reactants and the products of the electrochemical cell reach equilibrium, the value of ΔG becomes 0. At this point, the reaction quotient and the equilibrium constant (K_c) are the same. Since ΔG = -nFE, the cell potential at equilibrium is also 0.

Substituting the values of Q and E into the Nernst equation, the following equation is obtained.

0 = E⁰_cell – (RT/nF) ln K_c

The relationship between the Nernst equation, the equilibrium constant, and Gibbs energy change are illustrated below.

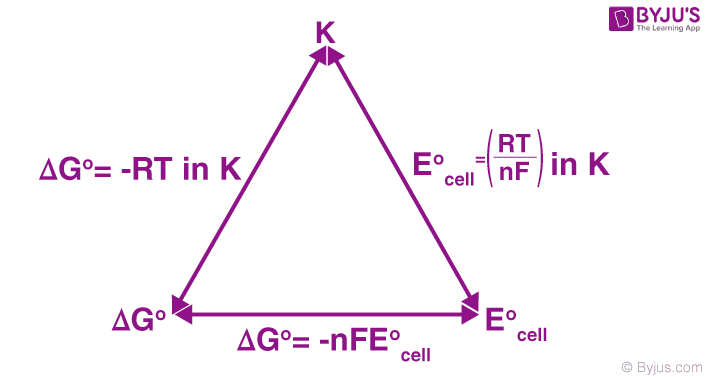
Nernst equation vs Equilibrium constant vs Gibbs energy change

Converting the natural logarithm into base-10 logarithm and substituting T = 298 K (standard temperature), the equation is transformed as follows.

E⁰_cell = (0.0592V/n) log K_c

By rearranging this equation, the following equation can be obtained.

log K_c = (nE⁰_cell)/0.0592V

Thus, the relationship between the standard cell potential and the equilibrium constant is obtained. When K_c is greater than 1, the value of E⁰_cell will be greater than 0, implying that the equilibrium favours the forward reaction. Similarly, when K_c is less than 1, E⁰_cell will hold a negative value which suggests that the reverse reaction will be favoured.

Nernst Equation Applications

The Nernst equation can be used to calculate the following:

• Single electrode reduction or oxidation potential at any conditions
• Standard electrode potentials
• Comparing the relative ability as a reductive or oxidative agent
• Finding the feasibility of combining such single electrodes to produce an electric potential
• Emf of an electrochemical cell
• Unknown ionic concentrations
• The pH of solutions and solubility of sparingly soluble salts can be measured with the help of the Nernst equation.

Limitations of Nernst Equation

The activity of an ion in a very dilute solution is close to infinity and can, therefore, be expressed in terms of the ion concentration. However, the ion concentration is not equal to the ion activity for solutions having very high concentrations. In order to use the Nernst equation in such cases, experimental measurements must be conducted to obtain the true activity of the ion.

Another shortcoming of this equation is that it cannot be used to measure cell potential when a current flows through the electrode. This is because the current flow affects the ions’ activity on the surface of the electrode. Also, additional factors such as resistive loss and overpotential must be considered when a current flows through the electrode.

Solved Examples on NERNST Equation

1. The standard electrode potential of zinc ions is 0.76V. What will be the potential of a 2M solution at 300 K?

Solution:

The Nernst equation for the given conditions can be written as follows:

EMⁿ⁺/M = E^o – [(2.303RT)/nF] × log 1/[Mn⁺]

Here,

• E° = 0.76V
• n = 2
• F = 96500 C/mole
• [Mn⁺] = 2 M
• R =8.314 J/K mole
• T =300 K

Substituting the given values in the Nernst equation, we get,

EZn²⁺/Zn = 0.76 – [(2.303×8.314×300)/(2×96500)] × log 1/2 = 0.76 – [0.0298 × (-0.301)]

= 0.76 + 0.009 = 0.769 V

Therefore, the potential of a 2 M solution at 300 K is 0.769 V.

2. From the following standard potentials, arrange the metals in the order of their increasing reducing power.

• Zn²⁺(aq) + 2e^– → Zn(s): E° = -0.76 V
• Ca²⁺(aq) + 2e^– → Ca(s): E° = -2.87 V
• Mg²⁺(aq) + 2e^– → Mg(s): E° = -2.36 V
• Ni²⁺(aq) + 2e^– → Ni(s): E° = -0.25 V
• Ni(s) → Ni2⁺(aq) + 2e^– : E° = +0.25 V

Reducing power of a metal increases with its ability to give up electrons, i.e., lower standard potentials. Arranging the reduction potentials in decreasing order gives the increasing order of reducing the power of metals.

Increasing order of reduction potentials is Ni (-0.25V) < Zn (-0.76V) < Mg(-2.36V) < Ca(-2.87).

3. What is the Cell Potential of the electrochemical cell in which the cell reaction is: Pb²⁺ + Cd → Pb + Cd²⁺? Given that E^o_cell = 0.277 volts, temperature = 25^oC, [Cd²⁺] = 0.02 M, and [Pb²⁺] = 0.2 M.

Solution

Since the temperature is equal to 25^oC, the Nernst equation can be written as follows:

E_cell = E⁰_cell – (0.0592/n) log₁₀Q

Here, two moles of electrons are transferred in the reaction. Therefore, n = 2. The reaction quotient (Q) is given by [Cd²⁺]/[Pb²⁺] = (0.02M)/(0.2M) = 0.1.

The equation can now be rewritten as:

E_cell = 0.277 – (0.0592/2) × log₁₀(0.1) = 0.277 – (0.0296)(-1) = 0.3066 Volts

Thus, the cell potential of this electrochemical cell at a temperature of 25^oC is 0.3066 volts.

4. The Cu²⁺ ion concentration in a copper-silver electrochemical cell is 0.1 M. If E^o(Ag⁺/Ag) = 0.8 V, E^o(Cu²⁺/Cu) = 0.34V, and Cell potential (at 25^oC) = 0.422 V. Find the silver ion concentration.

Solution

Here, the silver electrode acts as a cathode, whereas the copper electrode serves as the anode. This is because the standard electrode potential of the silver electrode is greater than that of the copper electrode. The standard electrode potential of the cell can now be calculated, as shown below:

E^o_cell = E^o_cathode – E^o_anode = 0.8V – 0.34V = 0.46V

Since the charge on the copper ion is +2 and the charge on the silver ion is +1, the balanced cell reaction is:

2Ag⁺ + Cu → 2Ag + Cu²⁺

Since two electrons are transferred in the cell reaction, n = 2, the Nernst equation for this electrochemical cell can be written as follows:

E_cell = E⁰_cell – (0.0592/2) × log(0.1/[Ag⁺]²)

0.422V = 0.46 – 0.0296 × (-1 – 2log[Ag⁺])

Therefore, -2log[Ag⁺] = 1.283 + 1 = 2.283

Or, log[Ag⁺] = -1.141