Electric potential energy is possessed by an object by virtue of two elements, those being the charge possessed by an object itself and the relative position of an object with respect to other electrically charged objects. The magnitude of electric potential depends on the amount of work done in moving the object from one point to another against the electric field.
Download Complete Chapter Notes of Electrostatic Potential and Capacitance
Download Now
When an object is moved against the electric field, it gains some amount of energy which is defined as the electric potential energy. For any charge, the electric potential is obtained by dividing the potential energy by the quantity of charge.
JEE Main 2021 LIVE Physics Paper Solutions 24-Feb Shift-1 Memory-based

Table of Contents
- Definition
- Formula
- Derivation
- Electric Potential of Point Charge
- Multiple Charges
- Important Points
- Solved Examples
What Is Electric Potential Energy?
The electric potential energy of any given charge or system of changes is defined as the total work done by an external agent in bringing the charge or the system of charges from infinity to the present configuration without undergoing any acceleration.
Definition: Electric potential energy is defined as the total potential energy a unit charge will possess if located at any point in outer space.
Overview
Electric potential energy is a scalar quantity and possesses only magnitude and no direction. It is measured in terms of Joules and is denoted by V. It has the dimensional formula of ML2T-3A-1.
| Electric Potential | |
| Denoted by | V, ∆V, U, ∆U |
| Dimension | ML2T-3A-1 |
| General Formula | Voltage = Energy/Charge |
| SI Unit | Volt |
There are two key elements on which the electric potential energy of an object depends:
- Its own electric charge.
- Its relative position with other electrically charged objects.
⇒ Also Read:
Electric Potential Formula
A charge placed in an electric field possesses potential energy and is measured by the work done in moving the charge from infinity to that point against the electric field. If two charges, q1 and q2, are separated by a distance d, the electric potential energy of the system is:
U = [1/(4πεo)] × [q1q2/d]
If two like charges (two protons or two electrons) are brought towards each other, the potential energy of the system increases. If two unlike charges, i.e., a proton and an electron, are brought towards each other, the electric potential energy of the system decreases.

Electric Potential Formula
Method 1:
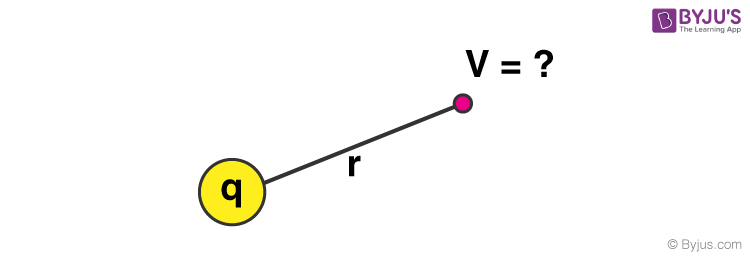
V = k × [q/r]
Where,
- V = electric potential energy
- q = point charge
- r = distance between any point around the charge to the point charge
- k = Coulomb constant, k = 9.0 × 109 N
Method 2: Using Coulomb’s Law

U = k × [q1q2/r2]
Where,
- U is the electrostatic potential energy
- q1 and q2 are the two charges
Note: The electric potential at infinity is zero (as r = ∞ in the above formula).
Electric Potential Derivation
Let us consider a charge q1. Let us say that they are placed at a distance ‘r’ from each other. The total electric potential of the charge is defined as the total work done by an external force in bringing the charge from infinity to the given point.
We can write it as, -∫ (ra→rb) F.dr = – (Ua – Ub)
Here, we see that the point rb is present at infinity, and the point ra is r.
Substituting the values, we can write, -∫ (r →∞) F.dr = – (Ur – U∞)
As we know that Uinfity is equal to zero.
Therefore, -∫ (r →∞) F.dr = -UR
Using Coulomb’s law between the two charges, we can write:
⇒ -∫ (r →∞) [-kqqo]/r2 dr = -UR
Or, -k × qqo × [1/r] = UR
Therefore, UR = -kqqo/r
Electric Potential of a Point Charge
Let us consider a point charge ‘q’ in the presence of another charge ‘Q’ with infinite separation between them.
UE (r) = ke × [qQ/r]
where, ke = 1/4πεo = Columb’s constant
Let us consider a point charge ‘q’ in the presence of several point charges Qi with infinite separation between them.
UE (r) = ke q × ∑ni = 1 [Qi /ri]
Electric Potential for Multiple Charges
In the case of 3 charges:
If three charges, q1, q2 and q3, are situated at the vertices of a triangle, the potential energy of the system is,
U =U12 + U23 + U31 = (1/4πεo) × [q1q2/d1 + q2q3/d2 + q3q1/d3]
In the case of 4 charges:
If four charges, q1, q2, q3 and q4, are situated at the corners of a square, the electric potential energy of the system is,
U = (1/4πεo) × [(q1q2/d) + (q2q3/d) + (q3q4/d) + (q4q1/d) + (q4q2/√2d) + (q3q1/√2d)]
Special Case:
In the field of a charge Q, if a charge q is moved against the electric field from a distance ‘a’ to a distance ‘b’ from Q, the work done is given by,
W = (Vb – Va) × q = [1/4πεo × (Qq/b)] – [1/4πεo × (Qq/a)] = Qq/4πεo[1/b – 1/a] = (Qq/4πεo)[(a-b)/ab]
Important Points
- At a point midway between two equal and opposite charges, the electric potential is zero, but the electric field is not zero.
- The electric potential at a point is said to be one volt if one joule of work is done in moving one Coloumb of the charge against the electric field.
- If a negative charge is moved from point A to B, the electric potential of the system increases.
- The reference level used to define electric potential at a point is infinity. It signifies that the force on a test charge is zero at the reference level.
- The surface of the earth is taken to be at zero potential since the earth is so huge that the addition or removal of charge from it will not alter its electrical state.
⇒ Check: Gauss law and its applications
What Is Electric Potential Difference?
In an electrical circuit, the potential between two points (E) is defined as the amount of work done (W) by an external agent in moving a unit charge (Q) from one point to another.
Mathematically we can say that,
E = W/Q
Where,
- E = Electrical potential difference between two points
- W = Work done in moving a charge from one point to another
- Q = Quantity of charge in coulombs
Electric Potential Energy – Video Lesson

Solved Examples on Electric Potential
Problem 1: A particle of mass 40 mg carrying a charge 5×10-9 C is moving directly towards a fixed positive point charge of magnitude 10-8 C. When it is at a distance of 10 cm from the fixed point charge, it has a velocity of 50 cm/s. At what distance from the fixed point charge will the particle come momentarily to rest? Is the acceleration constant during motion?
Solution:
If the particle comes to rest momentarily at a distance r from the fixed charge, from the conservation of energy, we have,
Total energy of the system = constant
(K.E + P.E) = constant
(1/2)mu2 + 1/4πεo × [Qq/a] = (1/4πεo) × [Qq/r]
Substituting the given data, we get
⇒ 1/2 × 40 × 10-6 × 1/2 × 1/2 = 9 × 109 × 10-8 × 5 × 10-9 × [ 1/r – 1/(10 × 10-2)]
or, [1/r – 10] = (5×10-5)/(9×5×10-8) = 100/9
or, 1/r = (100/9) + 10 = 190/9 m
i.e., r = 4.7 × 10-2 m
Since, F = [1/4πεo] × [Qq/r2]
Therefore, acceleration = F/m ∝ 1/r2, i.e., acceleration is not constant during motion.
Problem 2: A ball of mass 5 g and charge 10-7 C moves from point A, whose potential is 500 V, to point B, whose potential is zero. What is the velocity of the ball at point A if, at point B, it is 25 cm per second?
Solution:
Let u be the velocity of the ball at point A.
Work done on the charge by the field,
W = q × (VA – VB) = 10-7 × (500 – 0) = 5 × 10-5 J
This appears in the form of increased kinetic energy.
∴ W = (1/2) mv2 – (1/2) mu2
5 × 10-5 = (1/2) × 5/1000 [(1/4)2 – u2]
2 × 10-2 = 1/16 – u2
u2 = (1/16) – 0.02
= (1- 0.32)/16
= 0.0425
i.e., u =0.206 m/s = 20.6 cm/sec.
Therefore, u = 20.6 cm/sec.
Example 3: Let us say we have two charges of magnitude 1C and 2C placed at a distance of 2 metres from each other. Calculate the electric potential between these two charges. (Take: k = 1)
Solution:
Given that, the magnitude of charges is q1 = 1C and q2 = 2C.
The distance between these two charges is r = 2m.
The electric potential between these two charges is given by, Ur = -[kqqo]/r
Substituting the given values in the above equation, we get,
Ur = -1 J.
Example 4: How much work is required to be done in order to bring two charges of magnitude 3C and 5C from a separation of infinite distance to a separation of 0.5 m?
Solution:
∆E = E0 – Eg
= 0 – [-(9 × 109 × 5 × 3)/0.5] = 27 × 1010.
Therefore, ∆E = 27 × 1010.
You might also be interested in:
Recommended Videos
Electric Potential and Electric Potential Energy

Electric Potential Due to Dipole and System of Charges

Frequently Asked Questions on Electric Potential Energy
What is the electric potential difference?
In an electrical circuit, the potential between two points (E) is defined as the amount of work done (W) by an external agent in moving a unit charge (Q) from one point to another.
Mathematically we can say that,
E = W/Q
What is electric potential energy?
Electric potential energy is defined as the total potential energy a unit charge will possess if located at any point in outer space.
List a few examples of electric potential energy.
A non-functioning radio tower.
Before you switch on your car’s headlights.
A phone that has been switched off.

Comments