A simple pendulum can be described as a device where its point mass is attached to a light inextensible string and suspended from a fixed support. The vertical line passing through the fixed support is the mean position of a simple pendulum. The vertical distance between the point of suspension and the centre of mass of the suspended body, when it is in the mean position, is called the length of the simple pendulum, denoted by L. This form of the pendulum is based on the resonant system having a single resonant frequency.
Download Complete Chapter Notes of Simple Harmonic Motion
Download Now
Table of Contents
Simple Pendulum Definition
A simple pendulum is a mechanical arrangement that demonstrates periodic motion. The simple pendulum comprises a small bob of mass ‘m’ suspended by a thin string secured to a platform at its upper end of length L.
The simple pendulum is a mechanical system that sways or moves in an oscillatory motion. This motion occurs in a vertical plane and is mainly driven by gravitational force. Interestingly, the bob that is suspended at the end of a thread is very light; somewhat, we can say it is even massless. The period of a simple pendulum can be made extended by increasing the length string while taking the measurements from the point of suspension to the middle of the bob. However, it should be noted that if the mass of the bob is changed, the period will remain unchanged. The period is influenced mainly by the position of the pendulum in relation to Earth, as the strength of the gravitational field is not uniform everywhere.
In addition, pendulums are a common system whose usage is seen in various instances. Some are used in clocks to keep track of the time, while some are just used for fun in case of a child’s swing. In some cases, it is used in an unconventional manner, such as a sinker on a fishing line. In any case, we will explore and learn more about the simple pendulum on this page. We will discover the conditions under which it performs simple harmonic motion as well as derive an interesting expression for its period.
Important Terms
- The oscillatory motion of a simple pendulum: Oscillatory motion is defined as the to and fro motion of the pendulum in a periodic fashion, and the centre point of oscillation is known as the equilibrium position.
- The time period of a simple pendulum: It is defined as the time taken by the pendulum to finish one full oscillation and is denoted by “T”.
- The amplitude of a simple pendulum: It is defined as the distance travelled by the pendulum from the equilibrium position to one side.
- Length of a simple pendulum: It is defined as the distance between the point of suspension to the centre of the bob and is denoted by “l”.
⇒ Also Read:
Time Period of Simple Pendulum
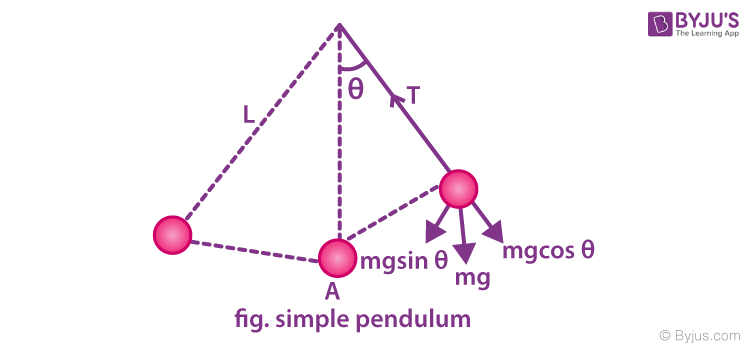
A point mass M is suspended from the end of a light inextensible string, whose upper end is fixed to a rigid support. The mass is displaced from its mean position.
Assumptions:
- There is negligible friction from the air and the system
- The arm of the pendulum does not bend or compress and is massless
- The pendulum swings in a perfect plane
- Gravity remains constant
Time Period of Simple Pendulum Derivation
Using the equation of motion, T – mg cosθ = mv2L
The torque tends to bring the mass to its equilibrium position,
τ = mgL × sinθ = mgsinθ × L = I × α
For small angles of oscillations sin θ ≈ θ,
Therefore, Iα = -mgLθ
α = -(mgLθ)/I
– ω02 θ = -(mgLθ)/I
ω02 = (mgL)/I
ω0 = √(mgL/I)
Using I = ML2, [where I denote the moment of inertia of bob]
we get, ω0 = √(g/L)
Therefore, the time period of a simple pendulum is given by,
T = 2π/ω0 = 2π × √(L/g)
Energy of Simple Pendulum
Potential Energy
The potential energy is given by the basic equation
Potential energy = mgh
m is the mass of the object
g is the acceleration due to gravity
h is the height of the object
However, the movement of the pendulum is not free fall; it is constrained by the rod or string. The height is written in terms of angle θ and length L. Thus, h = L(1 – cos θ)
When θ = 900, the pendulum is at the highest point. Then cos 900 = 0, and h = L.
Therefore,
Potential Energy = mgL
When θ = 00, the pendulum is at the lowest point. Then, cos 00 = 1. Therefore h = L (1-1) = 0
Potential energy = mgL (1-1) = 0
At all the points in between the potential energy is given as mgL (1 – cos θ).
Kinetic Energy
The kinetic energy of the pendulum is given as K.E = (1/2) mv2
m is the mass of the pendulum
v is the velocity of the pendulum
At the highest point, the kinetic energy is zero, and it is maximum at the lowest point. However, the total energy as a function of time is constant.
Mechanical Energy of the Bob
In a simple pendulum, the mechanical energy of the simple pendulum is conserved.
E = KE + PE= 1/2 mv2 + mgL (1 – cos θ) = constant
⇒ Note:
- If the temperature of a system changes, then the time period of the simple pendulum changes due to a change in the length of the pendulum.
- A simple pendulum is placed in a non-inertial frame of reference (accelerated lift, horizontally accelerated vehicle, vehicle moving along an inclined plane).
The mean position of the pendulum may change. In these cases, g is replaced by “g effective” for determining the time period (T).
For example,
- A lift moving upwards with acceleration ‘a’, then, T = 2π × √(L/geff) = 2π √[L/(g + a)]
- If the lift is moving downward with acceleration ‘a’, then T = 2π × √(L/geff) = 2π √[L/(g – a)]
- For a simple pendulum of length L is equal to the radius of the earth ‘R’, L = R = 6.4 x 106 m, then the time period T = 2π √R/2g
- For infinitely long pendulum L > > R near the earth surface, T = 2π × √(R/g)
Physical Pendulum
A simple pendulum is an idealised model. It is not achievable in reality. But the physical pendulum is a real pendulum in which a body of finite shape oscillates. From its frequency of oscillation, we can calculate the moment of inertia of the body about the axis of rotation.
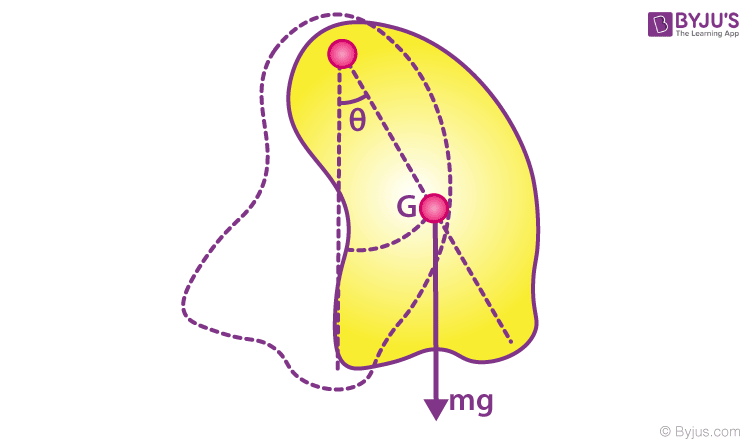
Consider a body of irregular shape and mass (m) that is free to oscillate in a vertical plane about a horizontal axis passing through a point, and weight mg acts downward at the centre of gravity (G).
⇒ Check: Centre of Mass of a System of Particles
If the body is displaced through a small angle (θ) and released from this position, a torque is exerted by the weight of the body to restore its equilibrium.
τ = -mg × (d sinθ)
τ = I α
I α = – mgdsinθ
I . d2θ/dt2 = – mgdsinθ
Where I = moment of inertia of a body about the axis of rotation.
d2θ/dt2 = (mgd/I) θ [Since, sinθ ≈ θ]
ω0 = √[mgd/I].
Time Period of Physical Pendulum
T = 2π/ω0 = 2π × √[I/mgd]
For ‘I’, applying the parallel axis theorem,
I = Icm + md2
Therefore, the time period of a physical pendulum is given by,
T = 2π × √[(Icm + md2)/mgd]
Related Video

Frequently Asked Questions on Simple Pendulum
What is a simple pendulum?
A simple pendulum is a point mass suspended by a weightless and inextensible string fixed rigidly to support.
What is an expression for the time period of a simple pendulum?
T = 2π√(l/g)
l is the length of the pendulum.
g is the acceleration due to gravity.
On what factors does the energy of the particle executing S.H.M. depend?
Mass of the particle.
Square of the amplitude of the particle.
Square of the frequency of the vibrating particle.
What is a second’s pendulum?
A second’s pendulum is a simple pendulum whose time period is 2 seconds.
When will the motion of a simple pendulum be simple harmonic motion?
The motion of a simple pendulum will be simple harmonic motion if its angular displacement θ is very small.
Will the time period increase or decrease when a pendulum is taken on top of the mountain?
The time period increases as ‘g’ decreases, so it gains time.
Why does a simple pendulum not vibrate at the centre of the earth?
At the centre of the earth, g = 0
Therefore, T = 2π√(l/g) = ∞
The pendulum will take infinite time to complete one vibration. In other words, the pendulum will not vibrate at the centre of the earth.
A vibrating simple pendulum of time period T is placed in a lift which is accelerating upwards. What will be the effect on the time period?
When the lift is accelerated upwards, the weight of the pendulum increases. The new weight (mg’) is given as
mg’ = mg + ma
g’ = g + a
The time period of the pendulum
T = 2π√(l/g) becomes
T’ = 2π√(l/g’)
Since g’ > g, so T’ < T
Therefore, the time period decreases.

Comments