NCERT Solutions bring out the very best in students through additional skill-building exercises that are tailored to their grade levels, abilities and interests. NCERT Solutions for Class 9 Maths includes solutions to all the questions covered under Chapter 8, Exercise 8.2. Download free NCERT Solutions for Maths, which help students fetch high marks in their board examinations.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals are solved by subject experts in simple and understandable language. BYJU’S provides step-by-step NCERT Class 9 Maths solutions for all the questions given in the textbook, as per CBSE board guidelines.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.2
Access other exercise solutions of Class 9 Maths Chapter 8 Quadrilaterals
Exercise 8.1 Solutions : 12 Solved Questions
Access Answers to Maths NCERT Class 9 Chapter 8 Quadrilateral Exercise 8.2
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
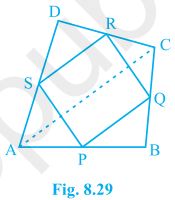
Solution:
(i) In ΔDAC,
R is the mid point of DC and S is the mid point of DA.
Thus, by mid point theorem, SR || AC and SR = ½ AC
(ii) In ΔBAC,
P is the mid-point of AB and Q is the mid point of BC.
Thus, by mid-point theorem, PQ || AC and PQ = ½ AC
also, SR = ½ AC
, PQ = SR
(iii) SR || AC ———————- from question (i)
and, PQ || AC ———————- from question (ii)
⇒ SR || PQ – from (i) and (ii)
also, PQ = SR
PQRS is a parallelogram.
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
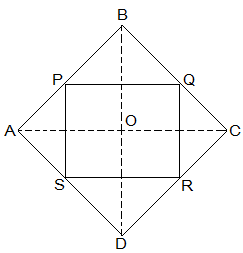
Given in the question,
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
To Prove,
PQRS is a rectangle.
Construction,
Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
, ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]———————- (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
, ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]———————- (ii)
Now,
In ΔCDB,
R and Q are the mid-points of CD and BC, respectively.
⇒ QR || BD
also,
P and S are the mid-points of AD and AB, respectively.
⇒ PS || BD
⇒ QR || PS
, PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
, PQRS is a rectangle.
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
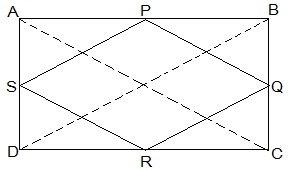
Given in the question,
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively.
Construction,
Join AC and BD.
To Prove,
PQRS is a rhombus.
Proof:
In ΔABC
P and Q are the mid-points of AB and BC, respectively
, PQ || AC and PQ = ½ AC (Midpoint theorem) — (i)
In ΔADC,
SR || AC and SR = ½ AC (Midpoint theorem) — (ii)
So, PQ || SR and PQ = SR
As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each other, so, it is a parallelogram.
, PS || QR and PS = QR (Opposite sides of parallelogram) — (iii)
Now,
In ΔBCD,
Q and R are mid-points of side BC and CD respectively.
, QR || BD and QR = ½ BD (Midpoint theorem) — (iv)
AC = BD (Diagonals of a rectangle are equal) — (v)
From equations (i), (ii), (iii), (iv) and (v),
PQ = QR = SR = PS
So, PQRS is a rhombus.
Hence Proved
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
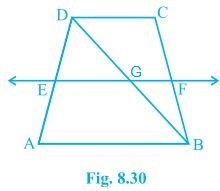
Solution:
Given that,
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD.
To prove,
F is the mid-point of BC.
Proof,
BD intersected EF at G.
In ΔBAD,
E is the mid-point of AD and also EG || AB.
Thus, G is the mid-point of BD (Converse of mid point theorem)
Now,
In ΔBDC,
G is the mid-point of BD and also GF || AB || DC.
Thus, F is the mid-point of BC (Converse of mid point theorem)
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD, respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
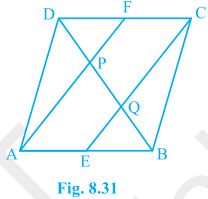
Solution:
Given that,
ABCD is a parallelogram. E and F are the mid-points of sides AB and CD, respectively.
To show,
AF and EC trisect the diagonal BD.
Proof,
ABCD is a parallelogram
, AB || CD
also, AE || FC
Now,
AB = CD (Opposite sides of parallelogram ABCD)
⇒½ AB = ½ CD
⇒ AE = FC (E and F are midpoints of side AB and CD)
AECF is a parallelogram (AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)
Now,
In ΔDQC,
F is mid point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ — (i)
Similarly,
In ΔAPB,
E is midpoint of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB — (ii)
From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Hence Proved.
6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
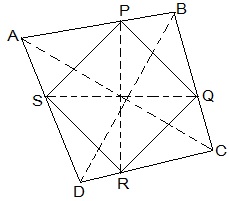
Let ABCD be a quadrilateral and P, Q, R and S are the mid points of AB, BC, CD and DA, respectively.
Now,
In ΔACD,
R and S are the mid points of CD and DA, respectively.
, SR || AC.
Similarly we can show that,
PQ || AC,
PS || BD and
QR || BD
, PQRS is parallelogram.
PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.
7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB
Solution:
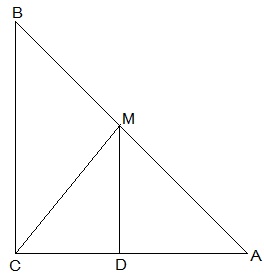
(i) In ΔACB,
M is the midpoint of AB and MD || BC
, D is the midpoint of AC (Converse of mid point theorem)
(ii) ∠ACB = ∠ADM (Corresponding angles)
also, ∠ACB = 90°
, ∠ADM = 90° and MD ⊥ AC
(iii) In ΔAMD and ΔCMD,
AD = CD (D is the midpoint of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
, ΔAMD ≅ ΔCMD [SAS congruency]
AM = CM [CPCT]
also, AM = ½ AB (M is midpoint of AB)
Hence, CM = MA = ½ AB
Chapter 8, Exercise 8.2 is based on the mid-point theorem, which is related to the mid-point of the sides of a triangle. All the questions listed under exercise 8.2 of NCERT Class 9 Maths Chapter 8 are based on the below-listed theorems,
- The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
- The line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.









It’s concept was very clear
This is very helpful 🙂🙂
Thanks for your help!!!
This was very helpful. Thanks a Lot 😃
Nice explanation
Thanku byjus😊😊
Nice
Great explaination
It’s very helpful 👍☺️
It was easy to understand and correct myself
Nice
Nice explanation
Thanks byjus
Thank you for helping🤗🤗🤗🤗
Very good answers