Circle Theorem- Chords

Circle Theorem:

A circle is the locus of all points in a plane which are equidistant from a fixed point. The fixed point is called the center of the circle and the constant distance between any point on the circle and its center is called the radius. The perimeter of a circle is known as circumference.

A line segment, which joins any two points on the circle’s circumference, is known as chord of the circle. Diameter is the largest chord which passes through center of the circle.

Figure 1 Circle

AB is a diameter, CD is a chord and OE is a radius of the circle.

Let us now look into properties exhibited by circles and study various circle theorem and their proofs.

Theorem 1: Two equal chords subtend equal angles at the center of the circle.

Figure 2

Proof: From fig. 2, In ∆AOB and ∆POQ

S. NoStatementReason1. AB = PQChords of equal length (Given)2. OA = OB = OP = OQRadii of the same circle3. ∆AOB ≅ ∆POQSSS Axiom of congruency4. ∠AOB = ∠POQFrom statement 3 (CPCT)

Note: CPCT stands for congruent parts of congruent triangles.

Converse of theorem 1 is also true, according to which if two angles subtended at center by two chords are equal then the chords are of equal length. From fig. 3, if ∠AOB = ∠POQ, then AB = PQ.

Figure 3

Proof:From fig. 3, In ∆AOB and ∆POQ

S. NoStatementReason1. ∠AOB = ∠POQEqual angle subtended at center O (Given)2. OA = OB = OP = OQRadii of the same circle3. ∆AOB ≅ ∆POQSAS Axiom of congruency4. AB = PQFrom statement 3 (CPCT)

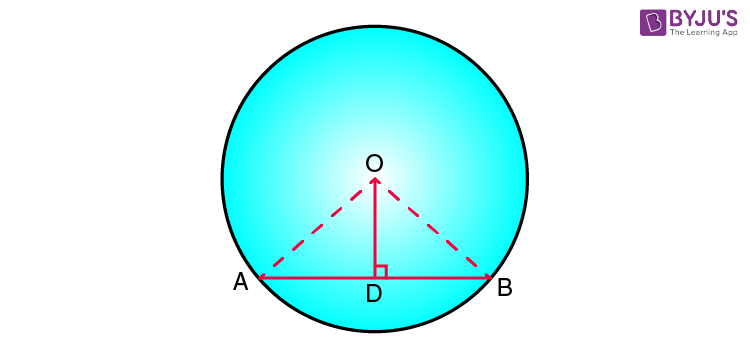
Theorem 2: The perpendicular to a chord, drawn from the center of the circle, bisects the chord.

In fig. 4, as OD⊥AB, therefore, AD = DB

Figure 4

Proof: From fig. 4, In ∆AOD and ∆BOD

S. NoStatementReason1. ∠ADO = ∠BDO = 90°OD ⊥ AB  (Given)2. OA = OBRadii of the same circle3. OD = ODCommon4. ∆AOB ≅ ∆POQR.H.S Axiom of congruency5. AD = DBFrom statement 4 (CPCT)

Converse of theorem 1 is also true, which states that a straight line passing through the center of a circle to bisect a chord is perpendicular to the chord.

Figure 5

Proof: From fig. 5, In ∆AOD and ∆BOD

S. NoStatementReason1. AD = DBOD  bisects (Given)2. OA = OBRadii of the same circle3. OD = ODCommon4. ∆AOB ≅ ∆POQSSS Axiom of congruency5. ∠ADO = ∠BDO = 90°From statement 4 (CPCT)

Theorem 3: Equal chords of a circle are equidistant from the center of the circle.

Figure 6

Construction: Join OB and OD

Proof: From fig. 6, In ∆OPB and ∆OQD

S. NoStatementReason1. BP =  1/2 ABTheorem 2: Perpendicular to chord bisects it2. DQ = 1/2 CDTheorem 2: Perpendicular to chord bisects it3. AB = CDGiven4. BP = DQFrom statements 1, 2 and 35. OB = ODRadii of the same circle6. ∠OPB = ∠OQD = 90°OP ⊥ AB and OQ ⊥ CD7. ∆OPB ≅ ∆OQDR.H.S Axiom of Congruency8. OP = OQCPCT

Converse of theorem 3, which states that chords of a circle, which are at equal distances from the center are equal in length is also true.

Proof: From fig. 6, In ∆OPB and ∆OQD

S. NoStatementReason1. OP = OQGiven2. ∠OPB = ∠OQD = 90° and3. OB = ODRadii of the same circle4. ∆OPB ≅ ∆OQDR.H.S Axiom of Congruency5. BP = DQCPCT6. 1/2 AB = 1/2 CDTheorem 2: Perpendicular from center bisects the chord⇒ Chord AB = Chord CD

Theorem 4: Measure of angles subtended to any point on the circumference of the circle from the same arc is equal to half of angle subtended at center by the same arc.From fig. 7 ∠AOB = 2∠APB

Figure 7

Construction: Join PD passing through center O

Proof:

S. No.StatementReasonIn ∆AOP1. OA = OPRadii of same circle2. ∠OAP = ∠OPAAngles opposite to equal sides of a triangle3. ∠AOD = ∠OAP + ∠OPAExterior Angle Property of triangle4. ∠AOD = 2∠OPAFrom statement 2:Similarly in ∆BOP5.Exterior ∠BOD = 2 ∠OPB 6.

∠AOB = ∠AOD + ∠BOD

⇒ ∠AOB = 2∠OPA + 2∠OPB

⇒ ∠AOB = 2(∠OPA + ∠OPB)

⇒ ∠AOB = 2∠APB

From statements 3 and 4

If ∠AOB is 180°, then ∠APB will be 90°. Also, in such a case AB will be the diameter of the circle passing through center O. This is also a theorem which can be stated as: Angle in a semi-circle is a right angle.

Figure 8

Theorem 5: In a cyclic quadrilateral, opposite angles are supplementary.

Note: A quadrilateral which is inscribed in a circle, i.e. all four vertices of the quadrilateral lie on circumference of the circle then such a quadrilateral is known as cyclic quadrilateral.

The converse of this theorem is also true which states that if opposite angles of a quadrilateral are supplementary then the quadrilateral is cyclic.

Figure 9

Proof: Consider the arc ADC

S. No.StatementReasonConsider arc ABC1. ∠AOC = 2∠ABC = 2αTheorem 4: Angle subtended by same arc is half of the angle subtended at the center.Consider arc ADC2. Reflex ∠AOC = 2 ∠ADC = 2βTheorem 4: Angle subtended by same arc is half of the angle subtended at the center.3.

∠AOC + Reflex ∠AOC = 360°

⇒ 2 ∠ABC + 2∠ADC = 360°

⇒ 2α + 2β = 360°

⇒α + β = 180°

Using statements  1 and 2.