In order to score high in Maths, RD Sharma Solutions are the best study materials for students. These solutions can be downloaded easily by clicking on the links provided here. The subject-matter experts at BYJU’S have prepared the RD Sharma Solutions to help the students who find it difficult to solve the given exercises. Chapter 18, Symmetry, includes three exercises. Students can easily access answers to the problems present in RD Sharma Solutions for Class 7. Let us have a look at some of the important concepts that are discussed in this chapter.
- Definition of symmetry
- Lines of symmetry
- Lines of symmetry of a line
- Lines of symmetry of a line segment
- Lines of symmetry of an angle
- Lines of symmetry of an isosceles triangle
- Lines of symmetry of a rhombus
- Lines of symmetry of rectangle
- Lines of symmetry of an isosceles trapezium
- Lines of symmetry of the kite
- Lines of symmetry of an arrowhead
- Lines of symmetry of a semi-circle
- Lines of symmetry of a circle
- Lines of symmetry of some regular polygons
- Lines of symmetry of an equilateral triangle
- Lines of symmetry of a square
- Lines of symmetry of a regular pentagon
- Lines of symmetry of a regular hexagon
- Line of symmetry and reflection
- Rotational symmetry
- Angle of rotation
- Order of rotational symmetry
RD Sharma Solutions for Class 7 Maths Chapter 18 Symmetry
Access Answers to Maths RD Sharma Solutions for Class 7 Chapter 18 – Symmetry
Exercise 18.1 Page No: 18.6
1. State the number of lines of symmetry for the following figures:
(i) An equilateral triangle
(ii) An isosceles triangle
(iii) A scalene triangle
(iv) A rectangle
(v) A rhombus
(vi) A square
(vii) A parallelogram
(viii) A quadrilateral
(ix) A regular pentagon
(x) A regular hexagon
(xi) A circle
(xii) A semi-circle
Solution:
(i) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore an equilateral triangle has 3 lines of symmetry.
(ii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore an isosceles triangle has 1 line of symmetry.
(iii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a scalene triangle has no line of symmetry.
(iv) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a rectangle has 2 lines of symmetry.
(v) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a rhombus has 2 lines of symmetry.
(vi) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a square has 4 lines of symmetry.
(vii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a parallelogram has no line of symmetry.
(viii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a quadrilateral has no line of symmetry.
(ix) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a regular pentagon has 5 lines of symmetry.
(x) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a regular hexagon has 6 lines of symmetry.
(xi) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a circle has an infinite number of lines of symmetry all along the diameters.
(xii) If a line divides a figure into two parts such that when the figure is folded about the line the two parts of the figure coincide, then the line is known as the line of symmetry.
Therefore a semicircle has only one line of symmetry.
2. What other name can you give to the line of symmetry of
(i) An isosceles triangle?
(ii) A circle?
Solution:
(i) An isosceles triangle has only 1 line of symmetry. This line of symmetry is also known as the altitude of an isosceles triangle.

(ii) A circle has infinite lines of symmetry all along its diameters.

3. Identify three examples of shapes with no line of symmetry.
Solution:



A scalene triangle, a parallelogram and a trapezium do not have any line of symmetry.
4. Identify multiple lines of symmetry, if any, in each of the following figures:

Solution:
(a)The given figure has 3 lines of symmetry. Therefore it has multiple lines of symmetry.

(b) The given figure has 2 lines of symmetry. Therefore it has multiple lines of symmetry.

(c) The given figure has 3 lines of symmetry. Therefore it has multiple lines of symmetry.

(d) The given figure has 2 lines of symmetry. Therefore it has multiple lines of symmetry.

(e) The given figure has 4 lines of symmetry. Therefore it has multiple lines of symmetry.

(f) The given figure has only 1 line of symmetry.

(g) The given figure has 4 lines of symmetry. Therefore it has multiple lines of symmetry.

(h) The given figure has 6 lines of symmetry. Therefore it has multiple lines of symmetry.

Exercise 18.2 Page No: 18.8
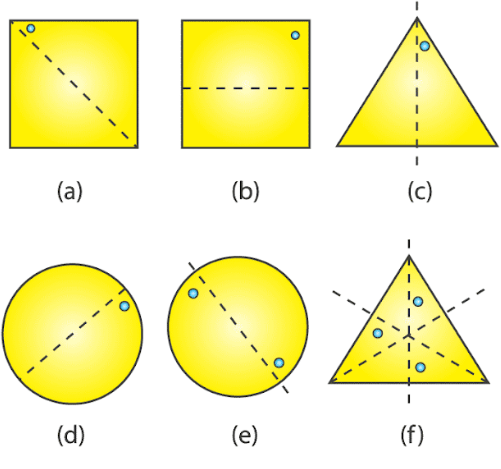
1. In the following figures, the mirror line (i.e. the line of symmetry) is given as dotted line. Complete each figure performing reflection in the dotted (mirror) line. Also, try to recall name of the complete figure.
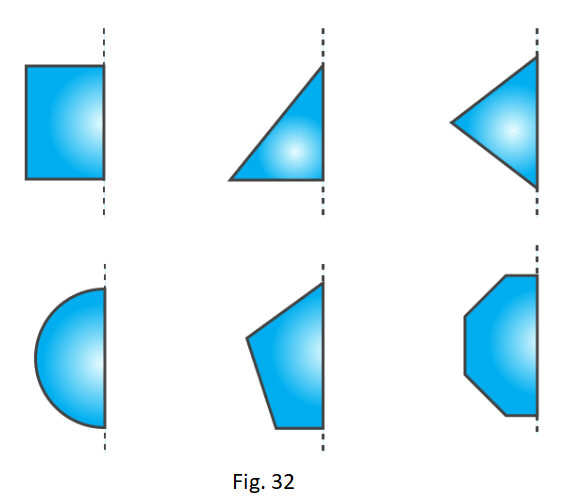
Solution:
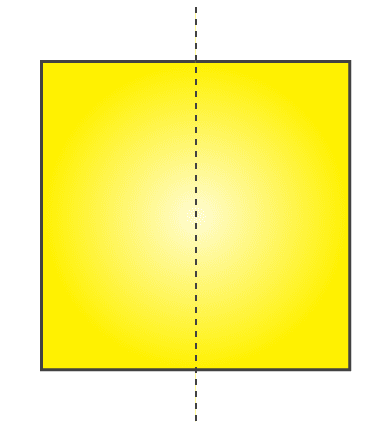
(a) It will be a rectangle.
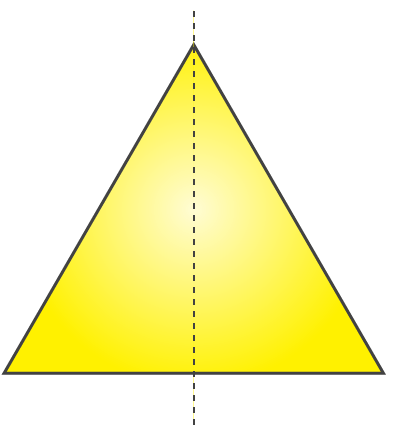
(b) It will be triangle
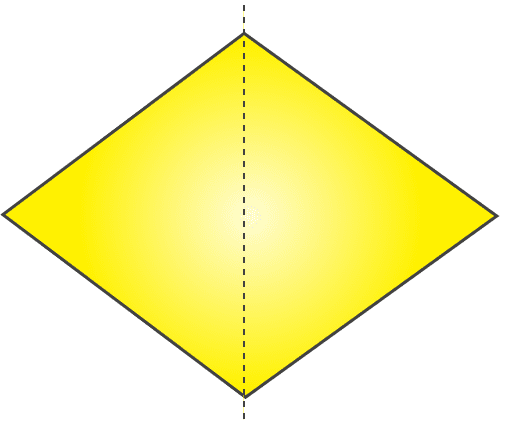
(c) It will be rhombus
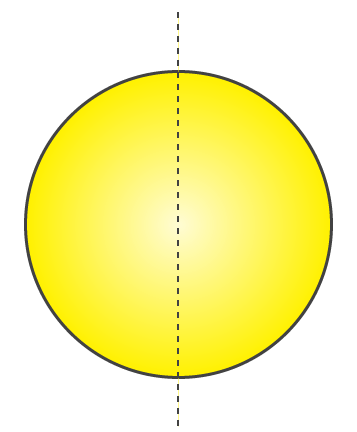
(d) It will be circle
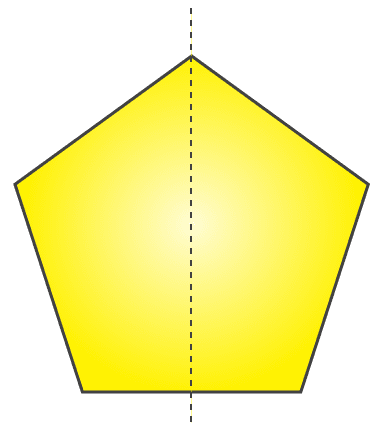
(e) It will be pentagon
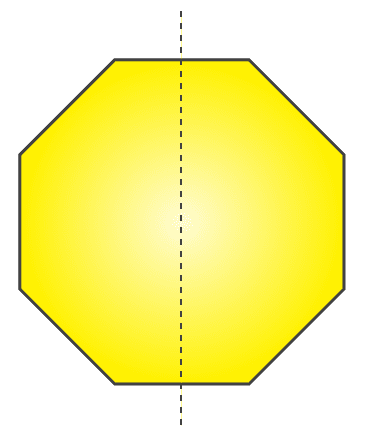
(d) It will be octagon
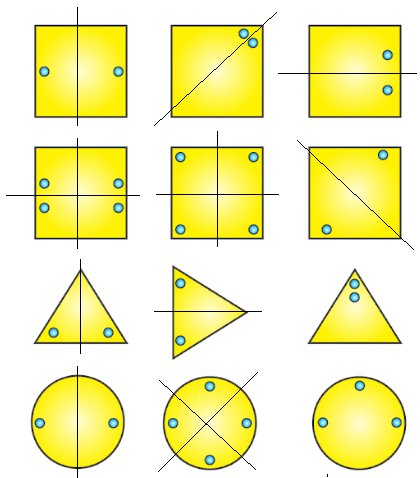
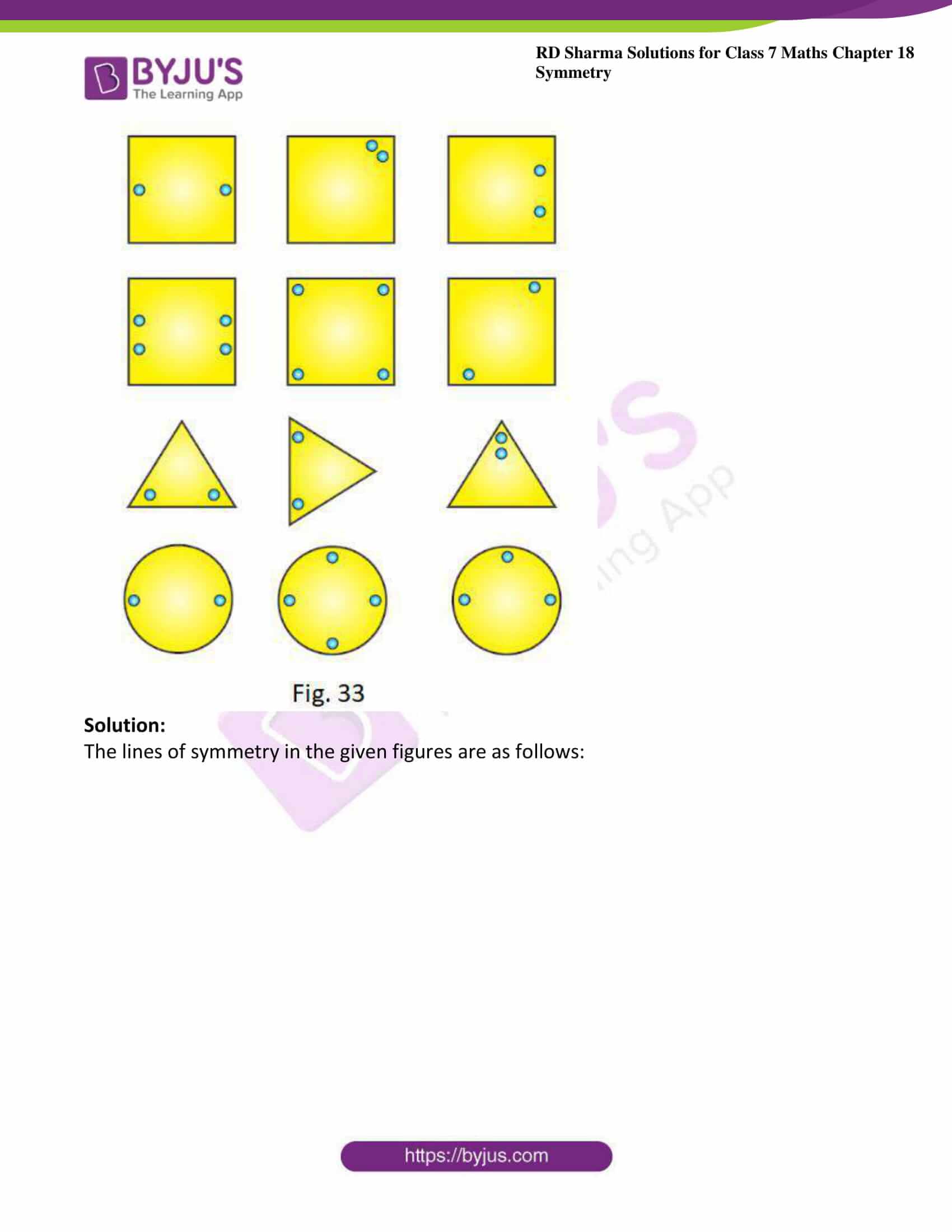
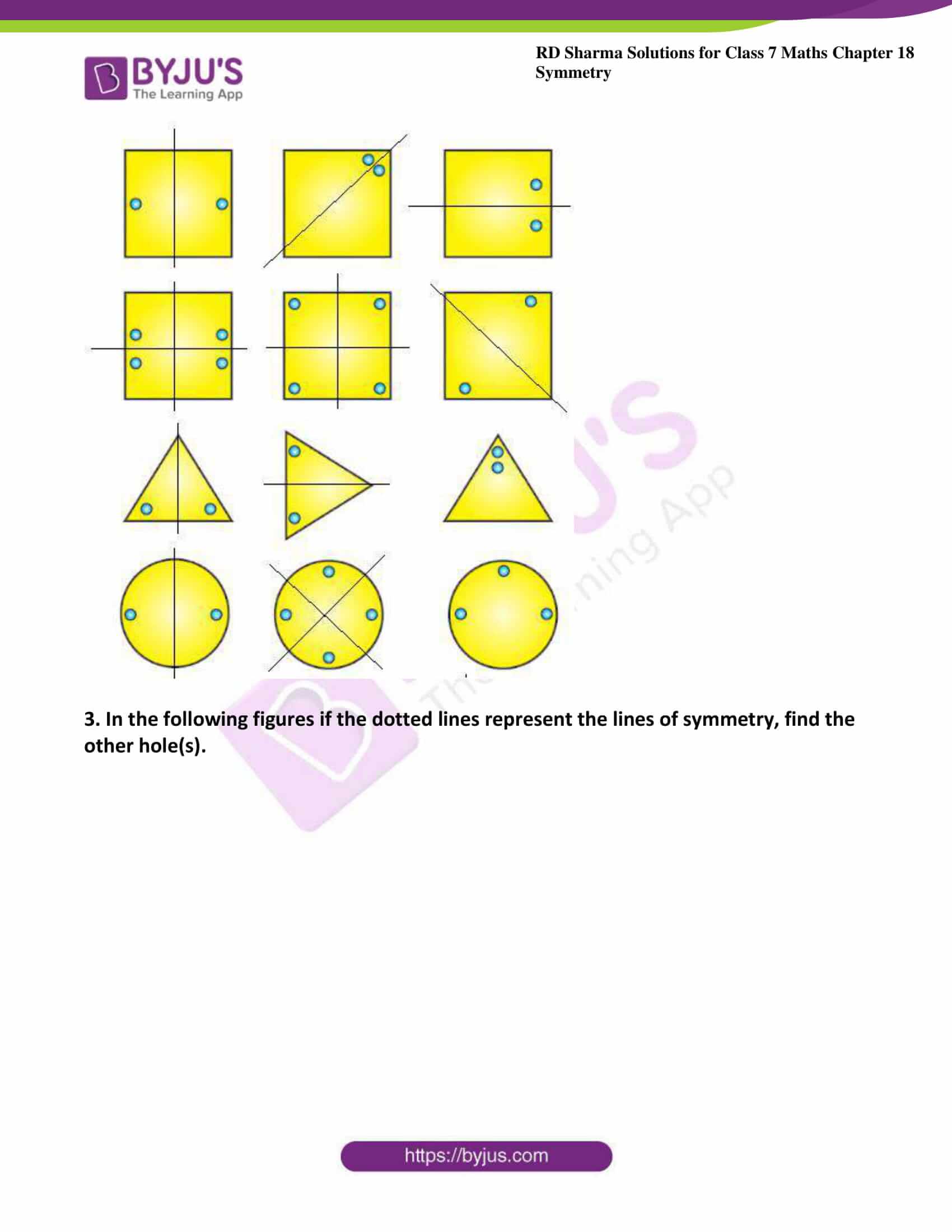
2. Each of the following figures shows paper cuttings with punched holes. Copy these figures on a plane sheet and mark the axis of symmetry so that if the paper is folded along it, then the wholes on one side of it coincide with the holes on the other side.
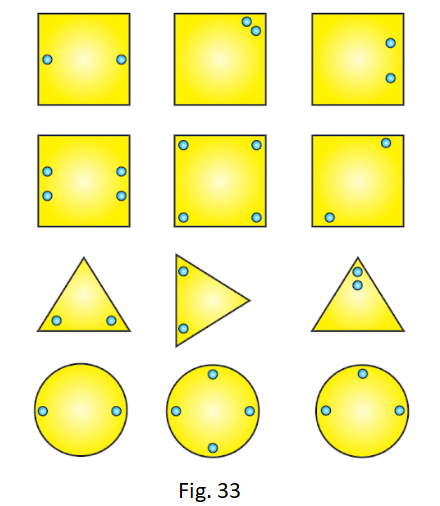
Solution:
The lines of symmetry in the given figures are as follows:
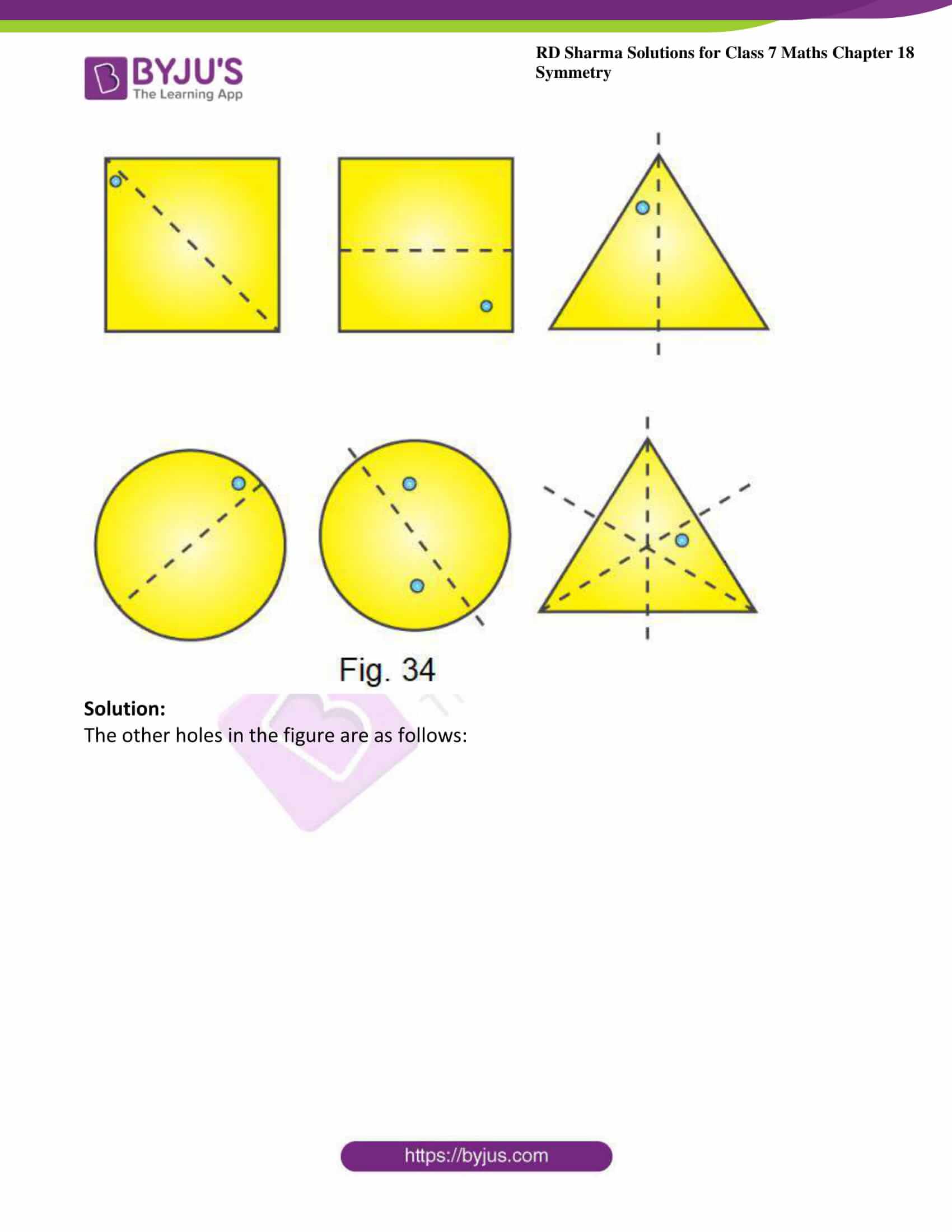
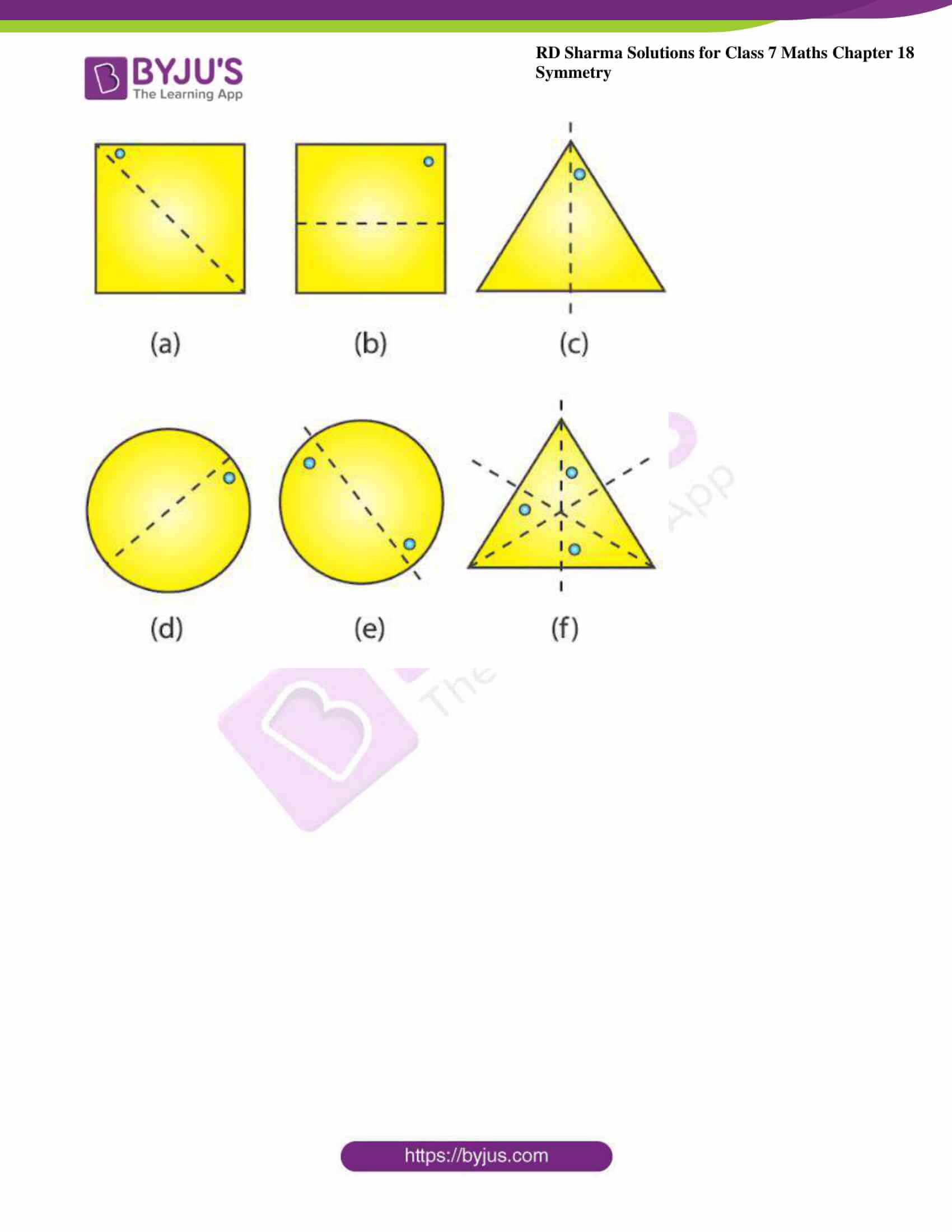
3. In the following figures if the dotted lines represent the lines of symmetry, find the other hole(s).
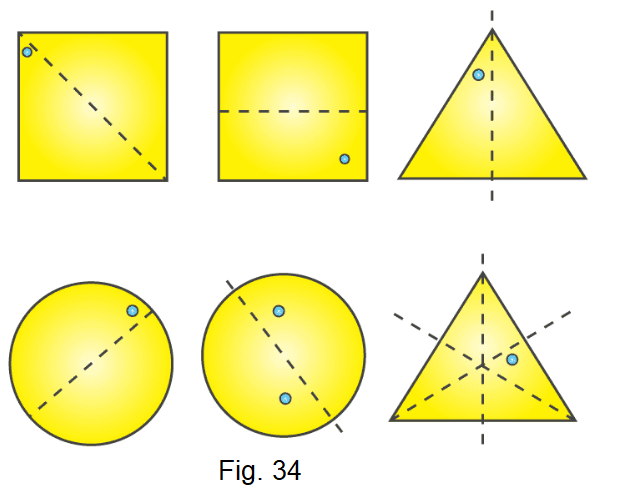
Solution:
The other holes in the figure are as follows:
Exercise 18.3 Page No: 18.16
1. Give the order of rotational symmetry for each of the following figures when rotated about the marked point (x):

Solution:
(i) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 4.
(ii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 3.
(iii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 3.
(iv) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 4.
(v) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 2.
(vi) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 4.
(vii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 5.
(viii) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 6.
(ix) A figure is said to have rotational symmetry if its fits onto itself more than once during a full turn that is rotation through 360o
Therefore the given figure has its rotational symmetry as 3.
2. Name any two figures that have both line symmetry and rotational symmetry.
Solution:
An equilateral triangle and a square have both lines of symmetry and rotational symmetry.

3. Give an example of a figure that has a line of symmetry but does not have rotational symmetry.
Solution:
A semicircle and an isosceles triangle have a line of symmetry but do not have rotational symmetry.

4. Give an example of a geometrical figure which has neither a line of symmetry nor a rotational symmetry.
Solution:
A scalene triangle has neither a line of symmetry nor a rotational symmetry.

5. Give an example of a letter of the English alphabet which has
(i) No line of symmetry
(ii) Rotational symmetry of order 2.
Solution:
(i) The letter of the English alphabet which has no line of symmetry is Z.
(ii) The letter of the English alphabet which has rotational symmetry of order 2 is N.
6. What is the line of symmetry of a semi-circle? Does it have rotational symmetry?
Solution:
A semicircle (half of a circle) has only one line of symmetry. In the figure, there is one line of symmetry. The figure is symmetric along the perpendicular bisector I of the diameter XY. A semi-circle does not have any rotational symmetry.

7. Draw, whenever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries.
(ii) a triangle with only line symmetry and no rotational symmetry.
(iii) a quadrilateral with a rotational symmetry but not a line of symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry.
Solution:
(i) An equilateral triangle has 3 lines of symmetry and a rotational symmetry of order 3.

(ii) An isosceles triangle has only 1 line of symmetry and no rotational symmetry.

(iii) A parallelogram is a quadrilateral which has no line of symmetry but a rotational symmetry of order 2.

(iv) A kite is a quadrilateral which has only one line of symmetry and no rotational symmetry.

8. Fill in the blanks:
| Figures | Centre of rotation | Order of rotation | Angle of rotation |
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral Triangle | |||
| Regular hexagon | |||
| Circle | |||
| Semi-circle |
Solution:
| Figures | Centre of rotation | Order of rotation | Angle of rotation |
| Square | Point of intersection of the line segments joining the mid-points of opposite sides. | 4 | 90o |
| Rectangle | Point of intersection of the line segments joining the mid-points of opposite sides | 2 | 180o |
| Rhombus | Point of intersection of diagonals | 2 | 180o |
| Equilateral Triangle | Point of intersection of angle bisectors i.e., centroid | 3 | 1200 |
| Regular hexagon | Centre of the hexagon | 6 | 60o |
| Circle | Centre of the circle | Unlimited | Any angle |
| Semi-circle | Nil | Nil | Nil |
9. Fill in the blanks:
| English Alphabet Letter | Line Symmetry | Number of Lines of Symmetry | Rotational symmetry | Order of rotational symmetry |
| Z | Nil | 0 | Yes | 2 |
| S | – | – | – | – |
| H | Yes | – | Yes | – |
| O | Yes | – | Yes | – |
| E | Yes | – | – | – |
| N | – | – | Yes | – |
| C | – | – | – | – |
Solution:
| English Alphabet Letter | Line Symmetry | Number of Lines of Symmetry | Rotational symmetry | Order of rotational symmetry |
| Z | Nil | 0 | Yes | 2 |
| S | Nil | 0 | Yes | 2 |
| H | Yes | 2 | Yes | 2 |
| O | Yes | 4 | Yes | 2 |
| E | Yes | 1 | No | 0 |
| N | Nil | 0 | Yes | 2 |
| C | Yes | 1 | No | 0 |















Comments