Get the free PDF of RD Sharma Solutions for Class 7 Maths Exercise 8.1 of Chapter 8 Linear Equation in One Variable, from the provided links. These PDFs can be easily downloaded by the students. Our subject experts have formulated these questions based on students’ grasping abilities. RD Sharma Solutions for Class 7 are the best study materials designed for CBSE students. This exercise includes linear equations. Some of the topics covered in this exercise are listed below.
- Equation – A statement of equality which involves one or more literal
- Linear equation – An equation in which the highest power of the variables involved is 1
- Solution of a linear equation
- Solving a linear equation by trial-and-error method
RD Sharma Solutions for Class 7 Maths Chapter 8 – Linear Equations in One variable Exercise 8.1
Access answers to Maths RD Sharma Solutions for Class 7 Chapter 8 – Linear Equation in One Variable Exercise 8.1
1. Verify by substitution that:
(i) x = 4 is the root of 3x – 5 = 7
(ii) x = 3 is the root of 5 + 3x = 14
(iii) x = 2 is the root of 3x – 2 = 8x – 12
(iv) x = 4 is the root of (3x/2) = 6
(v) y = 2 is the root of y – 3 = 2y – 5
(vi) x = 8 is the root of (1/2)x + 7 = 11
Solution:
(i) Given x = 4 is the root of 3x – 5 = 7
Now, substituting x = 4 in place of ‘x’ in the given equation, we get
= 3(4) – 5 = 7
= 12 – 5 = 7
7 = 7
Since, LHS = RHS
Hence, x = 4 is the root of 3x – 5 = 7.
(ii) Given x = 3 is the root of 5 + 3x = 14.
Now, substituting x = 3 in place of ‘x’ in the given equation, we get
= 5 + 3(3) = 14
= 5 + 9 = 14
14 = 14
Since, LHS = RHS
Hence, x = 3 is the root of 5 + 3x = 14.
(iii) Given x = 2 is the root of 3x – 2 = 8x – 12.
Now, substituting x = 2 in place of ‘x’ in the given equation, we get
= 3(2) – 2 = 8(2) – 12
= 6 – 2 = 16 – 12
4 = 4
Since, LHS = RHS
Hence, x = 2 is the root of 3x – 2 = 8x – 12.
(iv) Given x = 4 is the root of 3x/2 = 6.
Now, substituting x = 4 in place of ‘x’ in the given equation, we get
= (3 × 4)/2 = 6
= (12/2) = 6
6 = 6
Since, LHS = RHS
Hence, x = 4 is the root of (3x/2) = 6.
(v) Given y = 2 is the root of y – 3 = 2y – 5.
Now, substituting y = 2 in place of ‘y’ in the given equation, we get
= 2 – 3 = 2(2) – 5
= -1 = 4 – 5
-1 = -1
Since, LHS = RHS
Hence, y = 2 is the root of y – 3 = 2y – 5.
(vi) Given x = 8 is the root of (1/2)x + 7 = 11.
Now, substituting x = 8 in place of ‘x’ in the given equation, we get
= (1/2)(8) + 7 =11
= 4 + 7 = 11
= 11 = 11
Since, LHS = RHS
Hence, x = 8 is the root of 12x + 7 = 11.
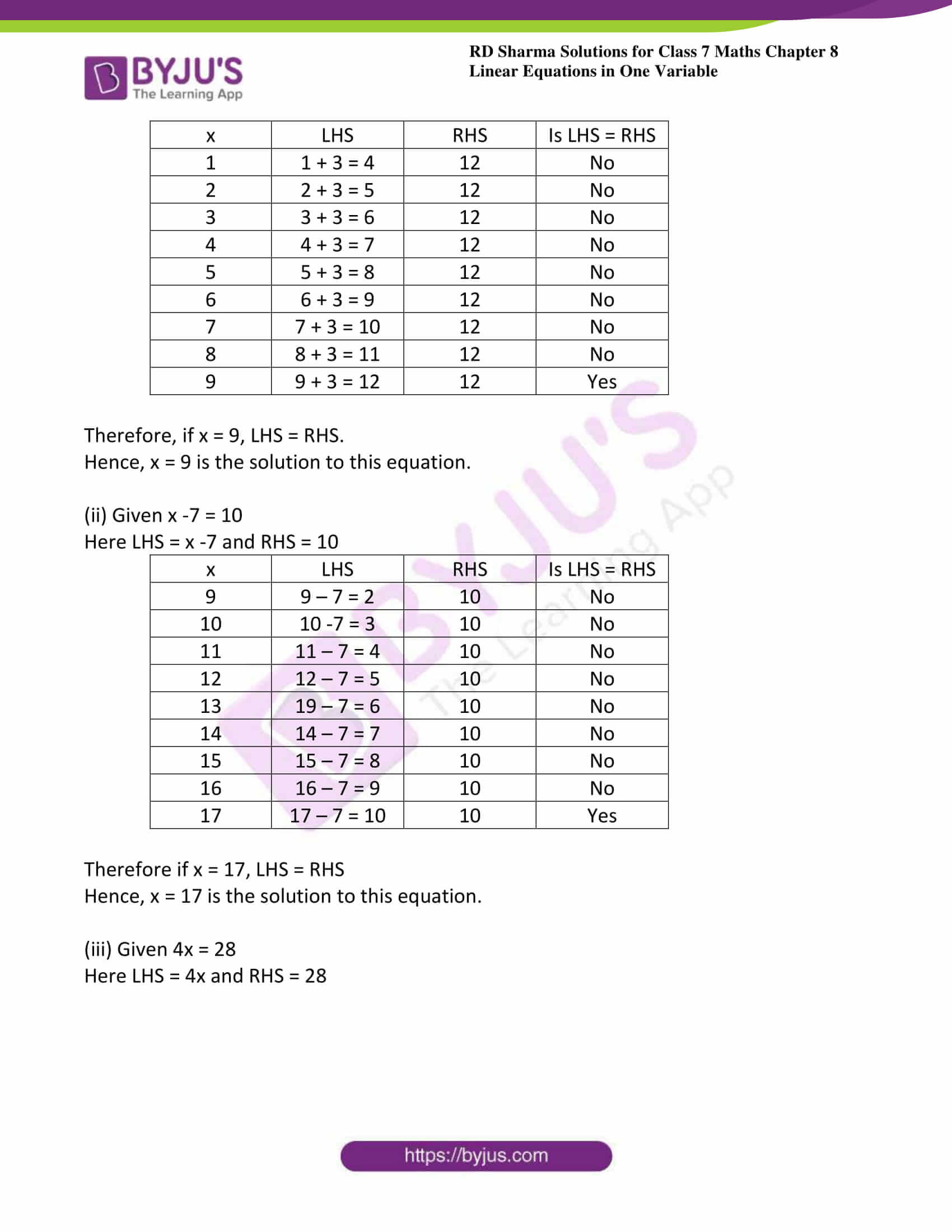
2. Solve each of the following equations by trial – and – error method:
(i) x + 3 =12
(ii) x -7 = 10
(iii) 4x = 28
(iv) (x/2) + 7 = 11
(v) 2x + 4 = 3x
(vi) (x/4) = 12
(vii) (15/x) = 3
(vii) (x/18) = 20
Solution:
(i) Given x + 3 =12
Here LHS = x +3 and RHS = 12
| x | LHS | RHS | Is LHS = RHS |
| 1 | 1 + 3 = 4 | 12 | No |
| 2 | 2 + 3 = 5 | 12 | No |
| 3 | 3 + 3 = 6 | 12 | No |
| 4 | 4 + 3 = 7 | 12 | No |
| 5 | 5 + 3 = 8 | 12 | No |
| 6 | 6 + 3 = 9 | 12 | No |
| 7 | 7 + 3 = 10 | 12 | No |
| 8 | 8 + 3 = 11 | 12 | No |
| 9 | 9 + 3 = 12 | 12 | Yes |
Therefore, if x = 9, LHS = RHS.
Hence, x = 9 is the solution to this equation.
(ii) Given x -7 = 10
Here LHS = x -7 and RHS = 10
| x | LHS | RHS | Is LHS = RHS |
| 9 | 9 – 7 = 2 | 10 | No |
| 10 | 10 -7 = 3 | 10 | No |
| 11 | 11 – 7 = 4 | 10 | No |
| 12 | 12 – 7 = 5 | 10 | No |
| 13 | 19 – 7 = 6 | 10 | No |
| 14 | 14 – 7 = 7 | 10 | No |
| 15 | 15 – 7 = 8 | 10 | No |
| 16 | 16 – 7 = 9 | 10 | No |
| 17 | 17 – 7 = 10 | 10 | Yes |
Therefore if x = 17, LHS = RHS
Hence, x = 17 is the solution to this equation.
(iii) Given 4x = 28
Here LHS = 4x and RHS = 28
| x | LHS | RHS | Is LHS = RHS |
| 1 | 4 × 1 = 4 | 28 | No |
| 2 | 4 × 2 = 8 | 28 | No |
| 3 | 4 × 3 = 12 | 28 | No |
| 4 | 4 × 4 = 16 | 28 | No |
| 5 | 4 × 5 = 20 | 28 | No |
| 6 | 4 × 6 = 24 | 28 | No |
| 7 | 4 × 7 = 28 | 28 | Yes |
Therefore if x = 7, LHS = RHS
Hence, x = 7 is the solution to this equation.
(iv) Given (x/2) + 7 = 11
Here LHS = (x/2) + 7 and RHS = 11
Since RHS is a natural number, (x/2) must also be a natural number, so we must substitute values of x that are multiples of 2.
| x | LHS | RHS | Is LHS = RHS |
| 2 | (2/2) + 7 = 1 + 7 =8 | 11 | No |
| 4 | (4/2) + 7 = 2 + 7 = 9 | 11 | No |
| 6 | (6/2) + 7 = 3 + 7 = 10 | 11 | No |
| 8 | (8/2) + 7 = 4 + 7 = 11 | 11 | Yes |
Therefore if x = 8, LHS = RHS
Hence, x = 8 is the solution to this equation.
(v) Given 2x + 4 = 3x
Here LHS = 2x + 4 and RHS = 3x
| x | LHS | RHS | Is LHS = RHS |
| 1 | 2 (1) + 4 = 2 + 4 = 6 | 3 (1) = 3 | No |
| 2 | 2 (2) + 4 = 4 + 4 = 8 | 3 (2) = 6 | No |
| 3 | 2 (3) + 4 = 6 + 4 = 10 | 3 (3) = 9 | No |
| 4 | 2 (4) + 4 = 8 + 4 = 12 | 3 (4) = 12 | Yes |
Therefore if x = 4, LHS = RHS
Hence, x = 4 is the solution to this equation.
(vi) Given (x/4) = 12
Here LHS = (x/4) and RHS = 12
Since RHS is a natural number, x/4 must also be a natural number, so we must substitute values of x that are multiples of 4.
| x | LHS | RHS | Is LHS = RHS |
| 16 | (16/4) = 4 | 12 | No |
| 20 | (20/4) = 5 | 12 | No |
| 24 | (24/4) = 6 | 12 | No |
| 28 | (28/4) = 7 | 12 | No |
| 32 | (32/4) = 8 | 12 | No |
| 36 | (36/4) = 9 | 12 | No |
| 40 | (40/4) = 10 | 12 | No |
| 44 | (44/4) = 11 | 12 | No |
| 48 | (48/4) = 12 | 12 | Yes |
Therefore if x = 48, LHS = RHS
Hence, x = 48 is the solution to this equation.
(vii) Given (15/x) = 3
Here LHS = (15/x) and RHS = 3
Since RHS is a natural number, 15x must also be a natural number, so we must substitute values of x that are factors of 15.
| x | LHS | RHS | Is LHS = RHS |
| 1 | (15/1) = 15 | 3 | No |
| 3 | (15/3) = 5 | 3 | No |
| 5 | (15/5) = 3 | 3 | Yes |
Therefore if x = 5, LHS = RHS
Hence, x = 5 is the solution to this equation.
(viii) Given (x/18) = 20
Here LHS = (x/18) and RHS = 20
Since RHS is a natural number, (x/18) must also be a natural number, so we must substitute values of x that are multiples of 18.
| x | LHS | RHS | Is LHS = RHS |
| 324 | (324/18) = 18 | 20 | No |
| 342 | (342/18) = 19 | 20 | No |
| 360 | (360/18) = 20 | 20 | Yes |
Therefore if x = 360, LHS = RHS
Hence, x = 360 is the solution to this equation.





Comments