According to the CBSE Syllabus 2023-24, this chapter has been removed from NCERT Class 12 Chemistry textbook.
1. Solids
Solids have definite volume, shape, and mass due to the short distance between the fixed position of particles and the strong interactions between them.
1.1 Characteristic Properties of the Solid State
(i) They have definite mass, volume and shape.
(ii) Intermolecular distances are short.
(iii) Intermolecular forces are strong.
(iv) Their constituent particles (atoms, molecules or ions) have fixed positions and can only oscillate about their mean positions.
(v) They are incompressible and rigid.
Students can refer to the short notes and MCQ questions along with separate solution pdf of this chapter for quick revision from the links below:
For more information on Solid State, watch the below videos


1.2 Amorphous and Crystalline Solids
Solids can be classified as crystalline or amorphous on the basis of the nature of order present in the arrangement of their constituent particles. Amorphous solids behave like super cool liquids as the arrangement of constituent particles has short-range order, is isotropic in nature and has no sharp melting point. Crystalline solids have a characteristic shape, with the arrangement of constituent particles of long-range order, anisotropic in nature and a sharp melting point.
1.3 Classification of Crystalline Solids
The classification of crystalline solids is based on their property. The crystalline property depends on the nature of interactions between the constituent particles, and therefore these solids are divided into four different categories:
- Ionic solids
- Covalent or Network solids
- Molecular solids
- Metallic solids

1.4 Crystal Lattices and Unit Cells
Unit Cell
The smallest repeating unit of the crystal lattice is the unit cell, the building block of a crystal.
Types Of Unit Cell
A lattice can be generated by repeating a small portion called the unit cell. Below are some of the different varieties of the unit cell:
- Primitive cubic unit cell
- Body-centered cubic unit cll
- Face-centred cubic unit cell

Crystal Lattices
A crystal structure is made of atoms. A crystal lattice is made of points. A crystal system is a set of axes. In other words, the structure is an ordered array of atoms, ions or molecules.
Characteristics of Crystal Lattice
(a) Each point in a lattice is called a lattice point or lattice site.
(b) Each point in a crystal lattice represents one constituent particle which may be an atom, a molecule (a group of atoms) or an ion.
(c) Lattice points are joined by straight lines to bring out the geometry of the lattice.
1.5 Number of Atoms in a Unit Cell
1.5.1 Primitive Cubic Unit Cell
The primitive cubic unit cell has atoms only at its corner. Each atom at a corner is shared between eight adjacent unit cells, four unit cells in the same layer, and four-unit cells in the upper or lower layer. Therefore, only 1/8th of an atom actually belongs to a particular unit cell.

1.5.2 Body-Centred Cubic Unit Cell
A body-centred cubic unit cell has an atom at each of its corners and also one atom at its body centre.

Number of Atoms in BCC Cell:
Thus, in a BCC cell, we have:
- 8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
- 1 body center atom = 1 × 1 = 1 atom
Therefore, the total number of atoms present per unit cell = 2 atoms.
1.5.3 Face-Centred Cubic Unit Cell
A face-centred cubic unit cell contains atoms at all the corners and at the centre of all the faces of the cube. The atom present at the face center is shared between 2 adjacent unit cells, and only 1/2 of each atom belongs to an individual cell.

Number of atoms in BCC cell
a) 8 corners × 18 per corner atom = 8 × 18 = 1 atom
b) 6 face-centered atoms × 12 atom per unit cell = 3 atoms
Hence, the total number of atoms in a unit cell = 4 atoms
Thus, in a face-centred cubic unit cell, we have:
- 8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
- 6 face-centered atoms × 1/2 atom per unit cell = 3 atoms
Therefore, the total number of atoms in a unit cell = 4 atoms.
1.6 Close-Packed Structures
In solids, the constituent particles are close-packed, leaving the minimum vacant space.
(a) Close Packing in One Dimension
In close packing of one dimension, spheres are arranged in a row such that adjacent atoms are in contact with each other. The coordination number is defined as the no. of nearest neighbour particles. In the case of one-dimension close packing, the coordination number is equal to two.

(b) Close Packing in Two Dimensions
In two-dimensional close packing, a row of closed-packed spheres is stacked to obtain a two-dimensional pattern.
This stacking is done in two ways:
Square Close Packing and Hexagonal Close Packing
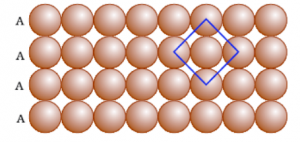
Packing in Solids: One and Two Dimensions
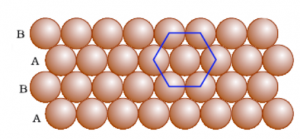
Hexagonal Close-Packing
(c) Close Packing in Three Dimensions

Crystalline solids exhibit a regular and repeating pattern of constituent particles. Three-dimensional closed packing are:
(i) Three-dimensional close packing forms two-dimensional square close-packed layers
(ii) Three-dimensional close packing from two-dimensional hexagonal close-packed layers.
1.6.1 Formula of a Compound and Number of Voids Filled
Voids literally mean gaps between constituent particles. Voids in solid states mean the vacant space between the constituent particles in a closed-packed structure.
There are two types of interstitial voids in a 3D structure:
Tetrahedral voids and Octahedral voids

Tetrahedral and Octahedral void
1.7 Packing Efficiency
Packing Efficiency is the percentage of total space filled by the particles.
1.7.1 Packing Efficiency in hcp and ccp Structures
Hexagonal close packing (hcp) and cubic close packing (ccp) have the same packing efficiency.
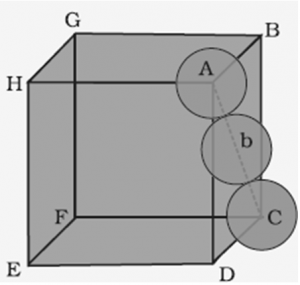
Packing Efficiency of a Unit Cell
1.7.2 Efficiency Packing in Body-Centred Cubic Structures
In a body-centred cubic unit cell, one atom is located at the body centre apart from the corners of the cube.
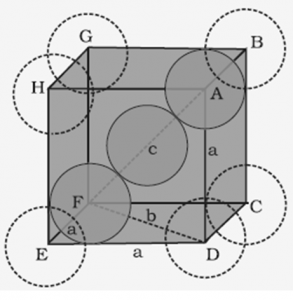
1.7.2 Packing Efficiency in Simple Cubic Lattice
In the simple cubic unit cell, atoms are located at the corners of the cube.

1.8 Calculations Involving Unit Cell Dimensions
The unit cell can be seen as a three-dimensional structure containing one or more atoms. We can determine the volume of this unit cell with the knowledge of the dimensions of the unit cell.
Mass of unit cell = number of atoms in unit cell × mass of each atom = z × m
Where, z = number of atoms in the unit cell, m = Mass of each atom
The mass of an atom can be given with the help of Avogadro number and molar mass as:
M/NA
Where M = molar mass
NA = Avogadro’s number
The volume of the unit cell, V = a3
=> Density of unit cell = mass of unit cell/ volume of the unit cell
=> Density of unit cell = m/V = z×ma/a3 = z×M/a3×NA
1.9 Imperfections in Solids
Point defects explain about the imperfections of solids along with the types of point defects. Point defects are accounted for when the crystallization process occurs at a very fast rate. These defects mainly happen due to deviation in the arrangement of constituting particles. The defects are of two types:
Point defects: Point defects are the irregularities or deviations from ideal arrangement around a point or an atom in a crystalline substance.
Line Defects: Line defects are irregularities or deviations from an ideal arrangement in entire rows of lattice points. These irregularities are called crystal defects.
1.9.1 Types of Point Defects
Point defects can be classified into three types:
1. Stoichiometric defect – In this kind of point defect, the ratio of positive and negative ions (Stoichiometric) and electrical neutrality of a solid is not disturbed. Sometimes it is also known as intrinsic or thermodynamic defects. Fundamentally, they are of two types: Vacancy defect and Interstitial defect
2. Frenkel defect – In ionic solids generally, the smaller ion (cation) moves out of its place and occupies an intermolecular space. In this case, a vacancy defect is created in its original position, and the interstitial defect is experienced at its new position.

3. Schottky defect – This kind of vacancy defects is found in Ionic Solids. But in ionic compounds, we need to balance the electrical neutrality of the compound so an equal number of anions and cations will be missing from the compound. It reduces the density of the substance. In this, the size of cations and anions is almost the same.

1.10 Electrical Properties
Solids can be classified into three types on the basis of their conductivities. They are:
(i) Conductors
(ii) Insulators
(iii) Semiconductors
1.11 Magnetic Properties
To study the magnetic properties of Magnetic Materials, the material is usually placed in a uniform magnetic field and then the magnetic field is varied. There are five major kinds of magnetic behaviour:
(i) Diamagnetic materials
(ii) Paramagnetic materials
(iii) Ferromagnetic materials
(iv) Antiferromagnetic materials
(v) Ferrimagnetic materials
Few Important Questions
- Explain the term coordination number.
- Distinguish between cubic close-packing and hexagonal close-packing.
- Explain why ionic solids are brittle and hard.
- Distinguish between a semiconductor and a conductor.
- Explain paramagnetism with a suitable example.
| Also Access |
| NCERT Solutions for Class 12 Chemistry Chapter 1 |
| NCERT Exemplar for Class 12 Chemistry Chapter 1 |
To discover more about this chapter, browse through these Solid State Class 12 Notes from BYJU’S.
To practise questions on Solid State, watch the below video

Other Important Links:
| Difference Between Isotropic And Anisotropic | Crystal Lattices and Unit Cells |
Frequently Asked Questions on CBSE Class 12 Chemistry Notes Chapter 1 Solid State
What are crystalline solids?
Crystalline solids are solids whose constituents are arranged in a highly ordered microscopic structure, forming a crystal lattice.
What is a unit cell?
A unit cell is the smallest portion of a crystal lattice that shows the three-dimensional pattern of the entire crystal.
What is packing efficiency?
The packing efficiency is the fraction of the crystal/unit cell actually occupied by the atoms.
Comments