Mensuration Class 6 Maths Notes - Chapter 10

Mensuration is a branch of mathematics which is a topic in geometry. It is a study of various geometrical shapes, their length, breadth, volume, and area for 2D as well as 3D shapes. Some important terminologies included in this topic are covered below.

Introduction to Mensuration

Mensuration

• Mensuration is the branch of mathematics that deals with the measurement of length, area or volume of various geometric shapes.

Shapes

• A shape is the form of an object.
• Examples of two-dimensional shapes are square, rectangle and triangle, and of three-dimensional shapes are cube, cuboid and sphere.

For more information on Solid Shapes, watch the below video

To know more about Mensuration, visit here.

Perimeter

• Perimeter is the total length or total distance covered along the boundary of a closed shape.

• Perimeter of a circle is also called as the circumference of the circle.

Perimeter of a Triangle

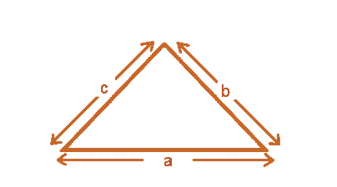
• Perimeter of triangle = Sum of lengths of all sides = a + b + c.
• If the given triangle is equilateral that is if all the sides are equal (a = b = c),
  then its perimeter is equal to 3 × length of one side of the triangle.

Perimeter of a Rectangle

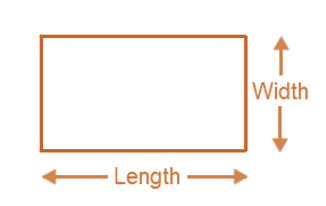
• Perimeter of the rectangle = length ( l ) + length ( l ) + width (w) + width (w)

= 2× [length ( l ) + width (w)]

Perimeter of a Square

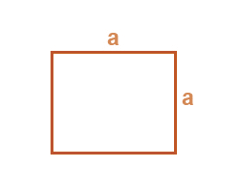
Perimeter of square = 4 × length of a side = 4a

Perimeter of an ‘n’ Sided Polygon

• A polygon is a closed shape made up of line segments.
• Perimeter of n sided polygon = n× length of one side.
• Example: Length of each side of a hexagon is a cm, then:
  Perimeter of the hexagon = 6a cm

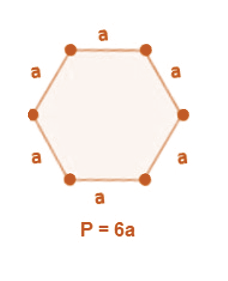
For more information on Perimeter, watch the below video

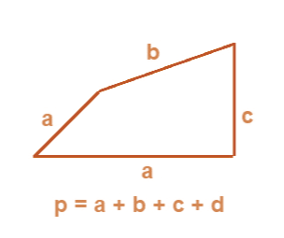
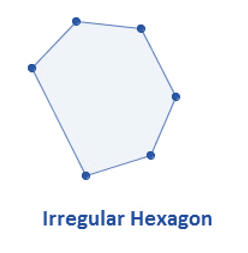
Perimeter of Irregular Sshapes

• Irregular shapes are the shapes which do not have all sides and angles equal.
• The perimeter of irregular shapes is equal to total length covered by the shape.
  In the figure given below, perimeter is the sum of all sides.

Area

• Area is the total amount of surface enclosed by a closed figure.

Area of Square

• Area of a square = Side × Side =Side²=a², where a is the length of each side.

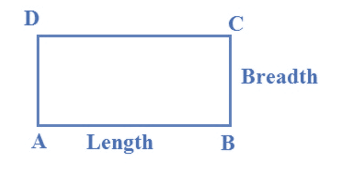
Area of Rectangle

•  Area = length ( l ) × breadth ( b)

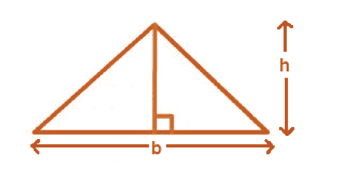
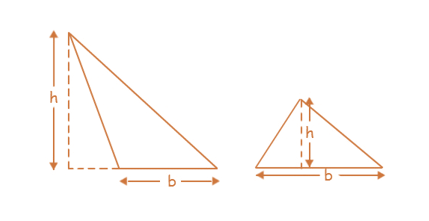
Area of Triangle

Area of triangle = (1/2) × base × height = (1/2) × b × h

To know Mensuration Formulas, visit here.

Areas of different types of triangles

• Consider an acute and an obtuse triangle.
  Area of each triangle = (1/2) × base × height = (1/2) × b × h

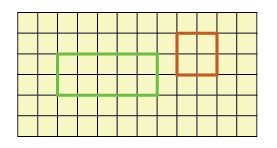
Visualisation of Area

• In the given graph, if the area of each small square is 1 cm², then
  Area of rectangle = l×b = 5×2 = 10cm²
  Area of square = a×a = 2×2 =4cm²

For more information on Visualisation of Areas, watch the below video

Area of Irregular Shapes

• • Area of an irregular figure can be calculated :
    Step 1: Divide the irregular shape into regular shapes that you can recognize (eg. triangles, rectangles, circles and squares)
    Step 2: Find the area of these individual shapes and add them. Sum will be the area of the irregular figure.

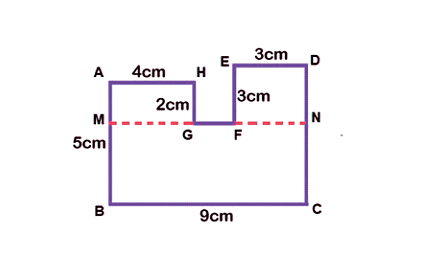
• • Example: Area of the given figure = Area of MNCB + Area of AMGH + Area of EFND
    = [ 5 × 9 + 4 × 2 + 3 × 3 ] cm²
    = [45 + 8 + 9 ] cm²
    =62 cm²

To solve questions on Mensuration, visit here.
Other Important Links: