According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 9.
Perimeter
- Perimeter is the total length or total distance covered along the boundary of a closed shape.

The perimeter of a Quadrilateral
For more information on Perimeter, watch the below video.

To know more about Perimeter, visit here.
Area
- The area is the total amount of surface enclosed by a closed figure.

Areas of a closed figure
For more information on Visualising Area, watch the below video.

The perimeter of Square and Rectangle
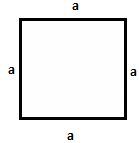
- Perimeter of a square = a + a + a + a = 4a, where a is the length of each side.
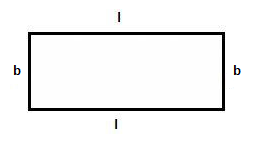
- Perimeter of a rectangle = l + l + b + b = 2(l + b), where l and b are length and breadth, respectively.
To know more about Perimeter Formula’s of All geometrical Figures, visit here.
Area of Square & Rectangle
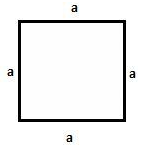
Area of square = 4a2
Here a is the length of each side
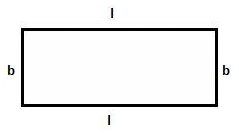
Area of rectangle = Length(l) × Breadth(b) = l×b
Area of a Parallelogram

- Area of parallelogram ABCD = (base×height)
Area of parallelogram ABCD = (b×h)
Triangle as Part of Rectangle
- The rectangle can be considered as a combination of two congruent triangles.
- Consider a rectangle ABCD, it is divided into 2 triangles ACD and ABD.

Triangles as parts of Rectangle - Area of each triangle = 12 (Area of the rectangle).
= 12(length×breadth)
= 12(10cm×5cm)
= 25cm2
Area of a Triangle
- Consider a parallelogram ABCD.
- Draw a diagonal BD to divide the parallelogram into two congruent triangles.
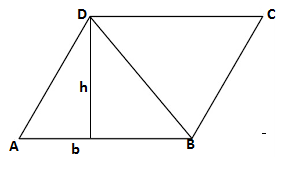
- Area of triangle ABD = 1/2 (Area of parallelogram ABCD)
Area of triangle ABD = 1/2 (b×h)
To know more about Area and Perimeter, visit here.
Conversion of Units
- Kilometres, metres, centimetres, millimetres are units of length.
- 10 millimetres = 1 centimetre
- 100 centimetres = 1 metre
- 1000 metres = 1 kilometre
Life of Pi
Terms Related to Circle
- A circle is a simple closed curve which is not a polygon.
- A circle is a collection of points which are equidistant from a fixed point.

- The fixed point in the middle is called the centre.
- The fixed distance is known as radius.
- The perimeter of a circle is also called as the circumference of the circle.
For more information on Terms Related to Circle, watch the below video.

Circumference of a Circle
- The circumference of a circle ( C ) is the total path or total distance covered by the circle. It is also called a perimeter of the circle.
Circumference of a circle = 2×π×r,
where r is the radius of the circle.
Visualising Area of a Circle
Area of Circle
- Area of a circle is the total region enclosed by the circle.
Area of a circle = π×r2, where r is the radius of the circle.
For more information on Area of Circle, watch the below video.

To know more about Circles, visit here.
Introduction and Value of Pi
- Pi (π) is the constant which is defined as the ratio of a circle’s circumference (2πr) to its diameter(2r).
π= Circumference (2πr)/Diameter (2r)
- The value of pi is approximately equal to 3.14159 or 22/7.
For more information on The Value Of Pi, watch the below video.

To know more about Value of Pi, visit here.
Problem Solving
Cost of Framing, Fencing
- Cost of framing or fencing a land is calculated by finding its perimeter.
- Example: A square-shaped land has length of its side 10m.
Perimeter of the land = 4 × 10 = 40m
Cost of fencing 1m = Rs 10
Cost of fencing the land = 40 m × Rs 10 = Rs 400
Cost of Painting, Laminating
- Cost of painting a surface depends on the area of the surface.
- Example: A wall has dimensions 5m×4m.
Area of the wall = 5m×4m=20m2
Cost of painting 1m2 of area is Rs 20.
Cost of painting the wall =20m2×Rs 20=Rs 400
Area of Mixed Shapes
- Find the area of the shaded portion using the given information.
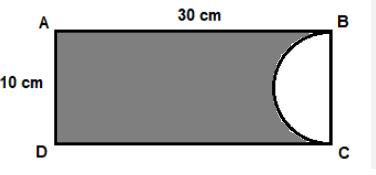
Solution: Diameter of the semicircle = 10cm
Radius of semicircle = 5cm
Area of the shaded portion = Area of rectangle ABCD – Area of semicircle
Area of the shaded portion = (l×b) − (πr2/2)
= 30×10 − (π×52/2)
= 300 − (π×25/2)
= (600 – 25π)/2
= (600 – 78.5)/2
= 260.7 cm2
Frequently Asked Questions on CBSE Class 7 Maths Notes Chapter 11 Perimeter and Area
What is value of pi?
The value of pi is 3.14159.
What is meant by area of a substance?
The amount of space taken up by any 2D shape is known to be the area covered by that substance.
What is the purpose of Unit conversion?
Unit conversion helps in the expression of the same property in different units of measurement. For example, time can be expressed in hours, minutes or seconds.
Every useful
Thank you byjus
Love you