Work And Energy Class 9 CBSE Notes - Chapter 11

Work

Work done on an object is defined as the product of the magnitude of the force acting on the body and the displacement in the direction of the force. W = F.s. The SI unit of force is Newton.

If a force acting on a body causes no displacement, the work done is 0. For example, pushing a wall.

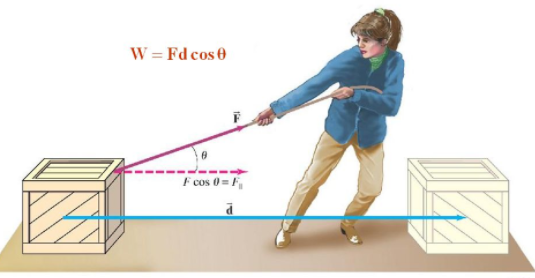
The force component F cos θ gives the component of force along the direction in that the body is displaced. Cos θ is the angle between the force vector and displacement vector.

To know more about Work, visit here.

Energy

Energy is defined as the ability to do work. Its unit is the same as that of work. Energy is a scalar quantity.

SI unit of energy or work = Joule (Nm) or $Kg{m}^2{s}^{-2}$.

Forms of Energy

Energy has different forms: Light, heat, chemical, electrical or mechanical.
Mechanical energy is the sum of
(i) Kinetic energy (K.E)
(ii) Potential energy (P.E)

To know more about Energy and Its Types, visit here.

Kinetic Energy

Objects in motion possess energy and can do work. This energy is called Kinetic Energy.

Also, From the second equation of motion, we know that Rearranging the equation, we get Substituting equation for work done by a moving body, Taking initial velocity as zero, we get

When two identical bodies are in motion, the body with a higher velocity has more KE.

To know more about Kinetic Energy, visit here.

Work-Energy Theorem

The work-energy theorem states that the net work done by a moving body can be calculated by finding the change in KE.

${\mathrm{\Rightarrow \; W}}_{net}=K{E}_{final}-\; KE initial$

${\mathrm{\Rightarrow W}}_{net}=$

m[v2−u2]

To know more about Work-Energy Theorem, visit here.

Factors Affecting Kinetic Energy

• Mass
• Velocity
• Momentum

Potential Energy

Energy can get stored in an object when work is done on it.

For example, stretching a rubber string. The energy that is possessed by a body by virtue of its configuration or change in position is known as Potential Energy.

The potential energy of an object at a height

When an object is raised to a certain height, work is done against gravity to change its position. This energy is stored as Potential Energy.

⇒W = F.s

⇒F = ma
In the case of increasing the height, F = mg
$Therefore,$ W (P.E) = mgh
$\mathrm{\Rightarrow \; \Delta }PE=mg(h_{final}-h_{initial})$

For more information on Kinetic and Potential Energy, watch the below video

To know more about Potential Energy, visit here.

Law of Conservation of Energy

Law of conservation of energy states that energy can neither be created nor destroyed but can be transferred from one form to another. The total energy before and after the transformation remains constant.

Total energy = KE + PE

where, 1/2 mv² + mgh = constant

For example: consider a ball falling freely from a height. At height h, it has only PE = mgh.

By the time it is about to hit the ground, it has a velocity and therefore has $KE=$

 mv2. Therefore, energy gets transferred from $PE$ to $KE,$ while the total energy remains the same.

To know more about the Law of Conservation of Energy, visit here.

Power

The rate of doing work or the rate of transfer of energy is called power. It is denoted by P

⇒ P =

SI unit is Watt $\left(J{s}^{-1}\right)$.

Average power $= \; Total energy consumed/Total time taken$

Commercial Unit of Power

The commercial unit of power is kWh, i.e. energy used in 1 hour at 1000 Joules/second.
$1kWh=3.6\times {10}^{6}J$