Geometry: Understanding Quadrilaterals

Introduction to Quadrilateral:

Figure 1 Quadrilateral

A 4 sided polygon bounded by 4 finite line segments is known as a quadrilateral. The word ‘quadrilateral’ is composed of two Latin words, quadri meaning ‘four ‘and latus meaning ‘side’. Hence, it is a two dimensional figure having four sides (or edges) and four vertices.

A diagonal is a line segment connecting the 2 non-consecutive vertices of a polygon. As it is known that based on diagonals, polygons can be classified as convex and concave.

In case of convex polygons, diagonals always lie inside the boundary of the polygon and in case of concave polygon one or more diagonals or a portion of it lies outside the boundary of polygon and also one or more interior angles of the polygon is reflex. Thus, classifying quadrilaterals based on diagonals, we have convex and concave quadrilaterals.

According to quadrilateral properties, the sum of interior angles of a quadrilateral is 360°. Let us try to prove this.

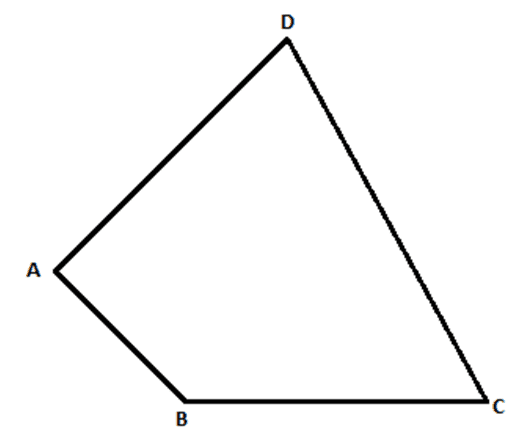
Proof: Consider a quadrilateral ABCD

Figure 2

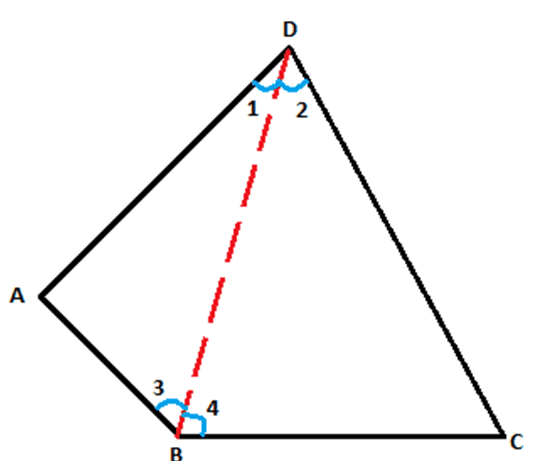
Constructions: Draw diagonal BD as shown:

Figure 3

From fig. 3;

∠B = ∠3 + ∠4 ….(1)

∠D = ∠1 + ∠2 ….(2)

In ∆ABD ∠A + ∠1 + ∠3 = 180° (Angle Sum Property of a triangle)

Similarly, in ∆BCD ∠C + ∠2 + ∠4 = 180° (Angle Sum Property of a triangle)

⇒ ∠A + ∠1 + ∠3 + ∠C + ∠2 + ∠4 = 360°

From equation (1) and (2), we have:

∠A + ∠B + ∠C + ∠D = 360°

Thus, it can be seen that the sum of interior angles in a quadrilateral is always 360°.

Also, the sum of exterior angles of a polygon is 360° always and; therefore, the sum of exterior angles of a quadrilateral is 360°.

Also, diagonal BD divides ABCD into two triangles, ∆ABD and ∆BCD. The measure of the sum of interior angles of ABCD is twice that of the sum of interior angles of a triangle i.e. 2 × 180°.

Based on lengths of sides and angles, types of convex quadrilaterals are:

• i) Parallelogram: Opposite sides are parallel and equal. Opposite angles are also equal. Diagonals bisect each other and pair of consecutive angles are supplementary.
  

  Figure 4 Parallelogram

• ii) Square: A parallelogram in which all sides are equal and each interior angle measures.
  

  Figure 5 Square

• iii) Rectangle: A parallelogram in which measure of all interior angles is and opposite sides are equal.
  

  Figure 6 Rectangle

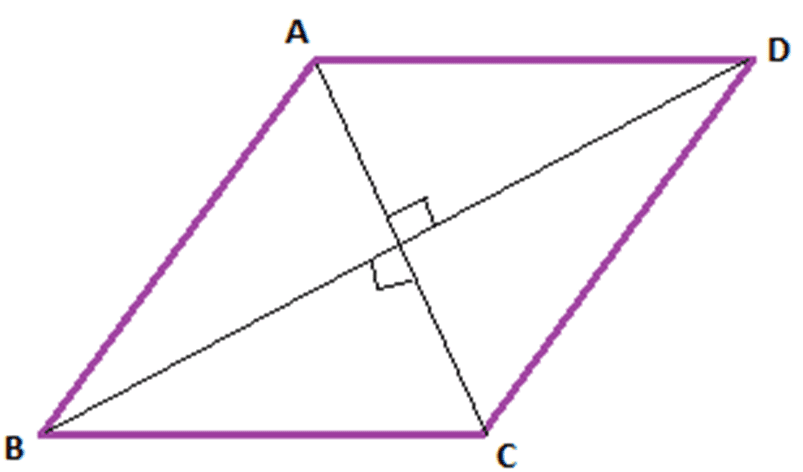
• iv) Rhombus: A parallelogram which has all four sides of equal measure and diagonals are perpendicular bisectors of each other.
  

  Figure 7 Rhombus

• v) Trapezoid: A quadrilateral with at least one pair of parallel sides.
  

  Figure 8 Trapezoid

• vi) Kite: A quadrilateral in which disjoint pair of adjacent sides is equal, and diagonals are perpendicular to each other.
  

  Figure 9 Kite

Let us now consider higher order polygons and try to figure out the sum of their interior angles.

Figure 10 Pentagon

Consider a pentagon as shown:

In pentagon PQRST, diagonals PR and PS divide the polygon into three triangles.

It can be seen that:

∠P = ∠1 + ∠2 + ∠3 ….(3)

∠R = ∠4 + ∠5 ….(4)

∠S = ∠6 + ∠7 ….(5)

Also in ∆PQR,∆PRS and ∆PST,

∠Q + ∠1 + ∠4 = 180°

∠2 + ∠5 + ∠6 = 180°

∠T + ∠3 + ∠7 = 180°

Adding the above three equations, we get:

∠Q + ∠1 + ∠4 + ∠2 + ∠5 + ∠6 + ∠T + ∠3 + ∠7 = 540°

From equations (3), (4) and (5):

∠P + ∠Q + ∠R + ∠S + ∠T = 540°

Thus, sum of interior angles of a pentagon is 540° which is thrice the sum of interior angles of a triangle i.e. 3 × 180°.

Consider a hexagon ABCDEF as shown and the sum of its interior angles can be figured out in similar way:

Figure 11 Hexagon

In hexagon ABCDEF, diagonals AC,AD and AE divide the polygon into four triangles.

From fig. 5:

∠A = ∠1 + ∠2 + ∠3 + ∠4 ….(6)

∠C = ∠5 + ∠6 ….(7)

∠D = ∠7 + ∠8 ….(8)

∠E = ∠9 + ∠10 ….(9)

From ∆ABC,∆ACD,∆ADE and ∆AEF and from equations (6), (7), (8) and (9) it can be seen that:

∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°

Thus, sum of interior angles of a hexagon is 540° which is four times the sum of interior angles of a triangle i.e. 4×180°.

So, the property can be generalized as:

In a n-sided polygon, the sum of interior angles is (n-2)×180°.

Also, for any n-sided polygon, the sum of exterior angles of any polygon is always 360°.

Thus for a regular polygon, measure of each exterior angle (∅) is given as:

∅ =

Understand Quadrilaterals with BYJU’s detailed video tutorial.’