NCERT Solutions for Class 6 Maths Chapter 4 Basic Geometrical Ideas are given here in downloadable PDF format. It is important for the students who are looking for the top score in their final exam to practise the questions from NCERT book class 6. While solving the questions, students might face several difficulties. Therefore, students are provided with NCERT Solutions for Class 6 Chapter 4, in accordance with the CBSE syllabus by our experts, to resolve their queries.
Download Exclusively Curated Chapter Notes for Class 6 Maths Chapter 4 – Basic Geometrical Ideas
Download Most Important Questions for Class 6 Maths Chapter 4 – Basic Geometrical Ideas
NCERT Solutions for Class 6 Maths Chapter 4: Basic Geometrical Ideas
The NCERT Solutions Class 6 Maths Basic Geometrical Ideas given here are extremely easy to understand and can help the students to clear all their doubts instantly. The solutions are explained with the best possible methods for each question. These solved questions will be helpful for the students to know the logic and ideas explained under the concept of geometry.
Access NCERT Solutions for Class 6 Chapter 4: Basic Geometrical Ideas
Exercise 4.1 Page no: 74
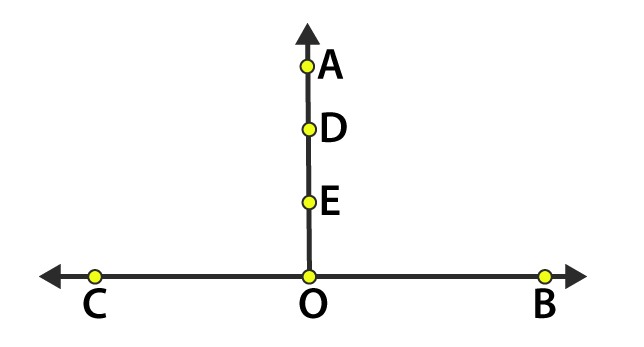
1. Use the figure to name:
(a) Five points
(b) A line
(c) Four rays
(d) Five line segments
Solutions:
(a) The five points are D, E, O, B and C
(b) A line is 
(c) Four rays are 
, 
, 
and 
.
(d) Five line segments are 
, 
, 
, 
and 
2. Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.
Solutions:
The lines are 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
3. Use the figure to name:
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies
(d) Two pairs of intersecting lines.
Solutions:
(a) Line containing point E is 
(b) Line passing through A is 
(c) Line on which O lies is 
(d) Two pairs of intersecting lines are 
, 
and 
, 
4. How many lines can pass through (a) one given point? (b) two given points?
Solutions:
(a) Countless lines can pass through a given point.
(b) Only one line can pass through two given points.
5. Draw a rough figure and label suitably in each of the following cases:
(a) Point P lies on
.
(b) 
and 
intersect at M.
(c) Line l contains E and F but not D.
(d) 
and 
meet at O.
Solutions:
(a)
(b)
(c)
(d)
6. Consider the following figure of line 
. Say whether following statements are true or false in context of the given figure.
(a) Q, M, O, N, P are points on the line 
.
(b) M, O, N are points on a line segment
.
(c) M and N are end points of line segment
.
(d) O and N are end points of line segment 
.
(e) M is one of the end points of line segment 
.
(f) M is point on ray 
.
(g) Ray
is different from ray
.
(h) Ray 
is same as ray
.
(i) Ray 
is not opposite to ray 
.
(j) O is not an initial point of 
(k) N is the initial point of 
and 
.
Solutions:
(a) True
(b) True
(c) True
(d) False
(e) False
(f) False
(g) True
(h) False
(i) False
(j) False
(k) True
Exercise 4.2 Page No: 78
1. Classify the following curves as (i) Open or (ii) Closed
Solutions:
(a) The given curve is an open curve
(b) The given curve is a closed curve
(c) The given curve is an open curve
(d) The given curve is a closed curve
(e) The given curve is a closed curve
2. Draw rough diagrams to illustrate the following:
(a) Open curve
(b) Closed curve
Solutions
(a) The below figure is an open curve
(b) The below figure is a closed curve
3. Draw any polygon and shade its interior.
Solutions:
The below figure is a polygon with a shaded interior.
4. Consider the given figure and answer the questions:
(a) Is it a curve?
(b) Is it closed?
Solutions:
(a) Yes, it is a curve
(b) Yes, it is a closed curve
5. Illustrate, if possible, each one of the following with a rough diagram:
(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.
Solutions:
(a) The below figure is a closed figure but not a polygon.
(b) The below figure is an open curve made up entirely of line segments.
(c) No, it’s not possible, as the polygon with the least number of sides is a triangle, which has three sides.
Exercise 4.3 Page no: 80
1. Name the angles in the given figure.
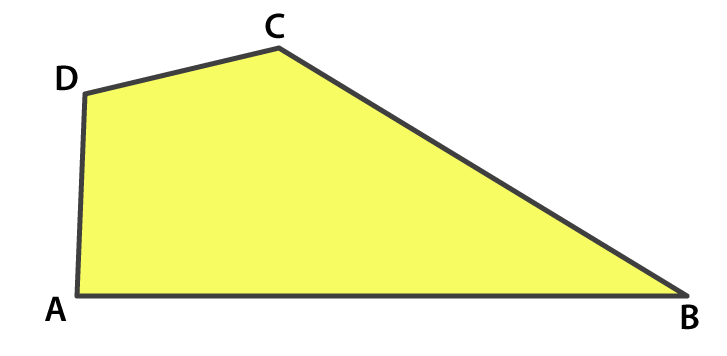
Solutions:
The angles are ∠DAB, ∠ABC, ∠BCD and ∠CDA
2. In the given diagram, name the points(s)
(a) In the interior of ∠DOE
(b) In the exterior of ∠EOF
(c) On ∠EOF
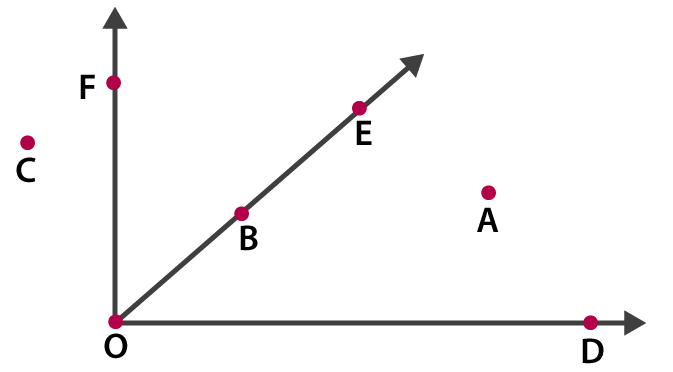
Solutions:
(a) The point in the interior of ∠DOE is A
(b) The points in the exterior of ∠EOF is C, A and D
(c) The points on ∠EOF are E, B, O and F
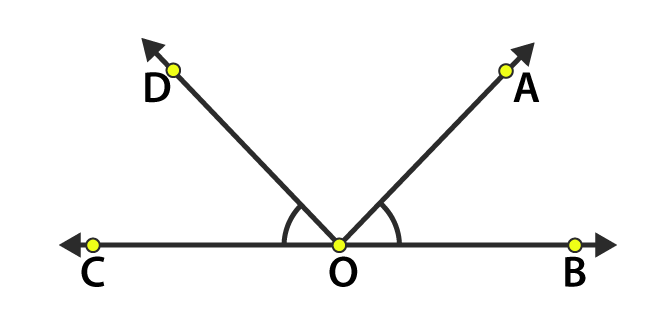
3. Draw rough diagrams of two angles such that they have
(a) One point in common
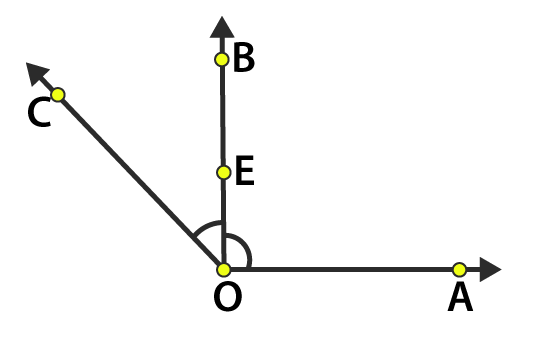
(b) Two points in common
(c) Three points in common
(d) Four points in common
(e) One ray in common
Solutions:
(a) O is the common point between ∠COD and ∠AOB
(b) O and B are common points between ∠AOB and ∠BOC
(c) O, E and B are common points between ∠AOB and ∠BOC
(d) O, E, D and A are common points between ∠BOA and ∠COA
(e) OC is a common ray between ∠BOC and ∠AOC
Exercise 4.4 page no: 81
1. Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior?
Solutions:
Point A lies on the given triangle ABC. It lies neither in the interior nor the exterior.
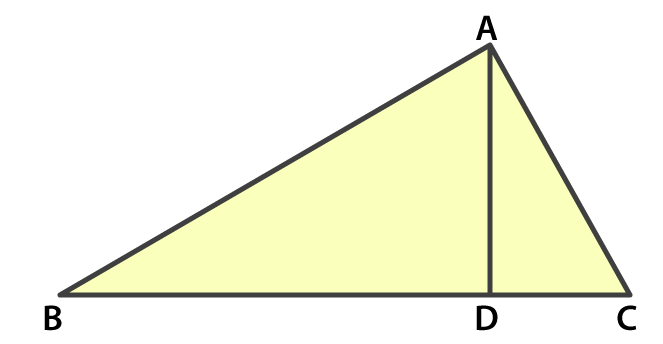
2. (a) Identify three triangles in the figure.
(b) Write the names of seven angles.
(c) Write the names of six line segments
(d) Which two triangles have ∠B as common?
Solutions:
(a) The three triangles are ∠ABD, ∠ACB, ∠ADC
(b) The angles are ∠BAC, ∠BAD, ∠CAD, ∠ADB, ∠ADC, ∠ABC, ∠ACB
(c) The line segments are 
, 
, 
, 
, 
, 
(d) ∠ABD and ∠ABC are triangles which have ∠B as common.
Exercise 4.5 Page no: 82
1. Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral?
Solutions:
PR and QS are the diagonals. They meet at point O, which is in the interior of the quadrilateral.
2. Draw a rough sketch of a quadrilateral KLMN. State,
(a) two pairs of opposite sides,
(b) two pairs of opposite angles,
(c) two pairs of adjacent sides,
(d) two pairs of adjacent angles.
Solutions:
(a) Two pairs of opposite sides are
, 
and 
, 
(b) Two pairs of opposite angles are ∠KLM, ∠KNM and ∠LKN, ∠LMN
(c) Two pairs of adjacent sides are
, 
and 
, 
or 
, 
and 
, 
(d) Two pairs of adjacent angles are ∠K, ∠L and ∠M, ∠N or ∠K, ∠L and ∠L, ∠M
Exercise 4.6 page no: 84
1. From the figure, identify:
(a) the centre of circle
(b) three radii
(c) a diameter
(d) a chord
(e) two points in the interior
(f) a point in the exterior
(g) a sector
(h) a segment
Solutions:
(a) The centre of the circle is O
(b) Three radii are 
, 
, 
(c) A diameter is 
(d) A chord is 
(e) Two points in the interior are O and P
(f) A point in the exterior is Q
(g) A sector is AOB, i.e., shaded region
(h) A segment is ED, i.e., shaded region
2. (a) Is every diameter of a circle also a chord?
(b) Is every chord of a circle also a diameter?
Solutions:
(a) Yes, every diameter of a circle is also a chord. The diameter is also called the longest chord.
(b) No, every chord is not a diameter.
3. Draw any circle and mark
(a) its centre
(b) a radius
(c) a diameter
(d) a sector
(e) a segment
(f) a point in its interior
(g) a point in its exterior
(h) an arc
Solutions:
(a) The centre of the circle is O.
(b) The radius is OC
(c) A diameter is 
(d) A sector is AOC
(e) A segment is DE
(f) A point in its interior is O
(g) A point in its exterior is F
(h) An arc is 
4. Say true or false:
(a) Two diameters of a circle will necessarily intersect.
(b) The centre of a circle is always in its interior.
Solutions:
(a) True, two diameters will always intersect each other at the centre of the circle.
(b) True, the centre of the circle will always be in its interior.
Disclaimer:Â
Dropped Topics – 4.11 Triangles, 4.12 Quadrilaterals, 4.13 Circles .
Frequently Asked Questions on NCERT Solutions for Class 6 Maths Chapter 4
What are the topics explained in Chapter 4 of NCERT Solutions for Class 6 Maths?
Basic Definitions in Geometry
Polygons
Triangles
Quadrilaterals
About Circles
Comments