According to the CBSE Syllabus 2023-24, this chapter has been removed from NCERT Class 6 Maths textbook.
Symmetry and Line of Symmetry Definition
The symmetry of an object is defined as one half of the object is a mirror image of the other half. When an object is split into half, both the sides are exactly the same. The line which divides them is called the line of symmetry. One simple example is reflection symmetry. The object can be divided into one or more than one lines of symmetry.
Below are some types of line of symmetry along with examples-
| S.NO | Type | Example |
| 1 | No line of symmetry | Scalene triangle |
| 2 | 1 line of symmetry | Isosceles triangle |
| 3 | 2 lines of symmetry | Rectangle |
| 4 | 3 lines of symmetry | Equilateral triangle |
Introduction to Symmetry
When figures have equally balanced proportions, they are said to be symmetrical.
For more information on Symmetry, watch the below video

To know more about Symmetry, visit here.
Bilateral Symmetry
If a figure is divided into two halves by only one line and these halves overlap each other completely, then the figure is said to have bilateral symmetry.
Example: A butterfly shows bilateral symmetry.

Line Symmetry
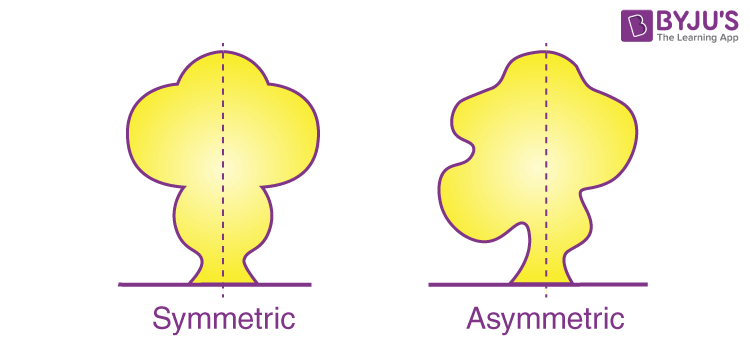
A figure has line symmetry if a line can be drawn dividing the figure into two symmetrical parts. The line is called a line of symmetry.
Example: The dotted lines in the following figures show line symmetry.

Lines of Symmetry
A figure can have any number of lines of symmetry passing through it. Some can have one, two or even multiple lines of symmetry.
Example of a single line of symmetry: A door lock.

Example of two lines of symmetry: A rectangle.

Example of multiple lines of symmetry (two or more): an equilateral triangle.

To know more about Line of Symmetry, visit here.
Point Symmetry and Reflection Symmetry
Reflection Symmetry
Reflection symmetry is very similar to line symmetry except for the change in orientation.

For example, when you view yourself in the mirror, your right hand becomes the left hand in the mirror.

Point Symmetry
Point symmetry exists when a figure is drawn around a single central point.
It is for figures having a point through which the symmetry can be established. This point is called the centre of symmetry.
For example, the hourglass shows point symmetry.

Kaleidoscope
A kaleidoscope uses mirrors to produce images that have several lines of symmetry.

Usually, two mirror strips forming a V-shape are used.
The angle between the mirrors determines the number of lines of symmetry.
The figure below shows the pattern formed by a kaleidoscope.

To know more about Kaleidoscope, visit here.
Other Important Links:
| Two Lines Symmetry | Scalene Triangle |
Frequently Asked Questions on CBSE Class 6 Maths Notes Chapter 13 Symmetry
What is symmetry?
In geometry, symmetry is defined as a balanced and proportionate similarity that is found in two halves of an object.
What are the different types of symmetry?
1. Translation 2. Rotation 3. Reflection 4. Glide reflection
What are the uses of kaleidoscope?
Some artists use a kaleidoscope to create new colour patterns and then draw them onto their canvas, it is very prominently used by designers to create patterns for rugs, clothes, jewellery, etc.
Comments