NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections Miscellaneous Exercise

*According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 10.

NCERT Solutions for Class 11 Maths are provided here to help the students in understanding the steps to solve mathematical problems that are in the Class 11 Maths NCERT textbook. Chapter 11 Conic Sections of Class 11 Maths is categorised under the CBSE Syllabus for the session 2023-24. The Miscellaneous Exercise of NCERT Solutions for Class 11 Maths Chapter 11- Conic Sections is based on the following topics:

1. Sections of a Cone
2. Circle
3. Parabola
4. Ellipse
5. Hyperbola

Each question of the exercise has been carefully solved for the students to understand, keeping the examination in mind. The NCERT Solutions for Class 11 Maths helps the students in understanding all the concepts of Class 11 Maths, in-depth.

NCERT Solutions for Class 11 Maths Chapter 11 – Conic Sections Miscellaneous Exercise

Download PDF

carouselExampleControls112

Previous





Next

Solutions for Class 11 Maths Chapter 11 – Miscellaneous Exercise

1. If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.

Solution:

We know that the origin of the coordinate plane is taken at the vertex of the parabolic reflector, where the axis of the reflector is along the positive x – axis.

Diagrammatic representation is as follows:

We know that the equation of the parabola is of the form y² = 4ax (as it is opening to the right)

Since, the parabola passes through point A(10, 5),

y² = 4ax

10² = 4a(5)

100 = 20a

a = 100/20

= 5

The focus of the parabola is (a, 0) = (5, 0), which is the mid – point of the diameter.

Hence, the focus of the reflector is at the mid-point of the diameter.

2. An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?

Solution:

We know that the origin of the coordinate plane is taken at the vertex of the arch, where its vertical axis is along the positive y –axis.

Diagrammatic representation is as follows:

The equation of the parabola is of the form x² = 4ay (as it is opening upwards).

It is given that at base arch is 10 m high and 5 m wide.

So, y = 10 and x = 5/2 from the above figure.

It is clear that the parabola passes through point (5/2, 10)

So, x² = 4ay

(5/2)² = 4a(10)

4a = 25/(4×10)

a= 5/32

we know the arch is in the form of a parabola whose equation is x² = 5/8y

We need to find width, when height = 2 m.

To find x, when y = 2.

When, y = 2,

x² = 5/8 (2)

= 5/4

x = √(5/4)

= √5/2

AB = 2 × √5/2 m

= √5m

= 2.23 m (approx.)

Hence, when the arch is 2 m from the vertex of the parabola, its width is approximately 2.23 m.

3. The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m.
Find the length of a supporting wire attached to the roadway 18 m from the middle.

Solution:

We know that the vertex is at the lowest point of the cable. The origin of the coordinate plane is taken as the vertex of the parabola, while its vertical axis is taken along the positive y –axis.

Diagrammatic representation is as follows:

Here, AB and OC are the longest and the shortest wires, respectively, attached to the cable.

DF is the supporting wire attached to the roadways, 18 m from the middle.

So, AB = 30 m, OC = 6m, and BC = 50 m.

The equation of the parabola is x² = 4ay (as it is opening upwards).

The coordinates of point A are (50, 30 -6) = (50, 24)

Since, A(50, 24) is a point on the parabola.

y² = 4ax

(50)² = 4a(24)

a = (50×50)/(4×24)

= 625/24

Equation of the parabola, x² = 4ay = 4×(625/24)y or 6x² = 625y

The x – coordinate of point D is 18.

Hence, at x = 18,

6(18)² = 625y

y = (6×18×18)/625

= 3.11 (approx.)

Thus, DE = 3.11 m

DF = DE +EF = 3.11 m +6 m = 9.11 m

Hence, the length of the supporting wire attached to the roadway 18 m from the middle is approximately 9.11 m.

4. An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.

Solution:

Since, the height and width of the arc from the centre is 2 m and 8 m, respectively, it is clear that the length of the major axis is 8 m, while the length of the semi- minor axis is 2 m.

The origin of the coordinate plane is taken as the centre of the ellipse, while the major axis is taken along the x-axis.

Hence, Diagrammatic representation of semi- ellipse is as follows:

The equation of the semi – ellipse will be of the from x²/16 + y²/4 = 1, y ≥ 0 … (1

Let A be a point on the major axis such that AB = 1.5m.

Now draw AC ⊥ OB.

OA = (4 – 1.5)m = 2.5m

The x – coordinate of point C is 2.5

On substituting the value of x with 2.5 in equation (1), we get,

(2.5)²/16 + y²/4 = 1

6.25/16 + y²/4 = 1

y² = 4 (1 – 6.25/16)

= 4 (9.75/16)

= 2.4375

y = 1.56 (approx.)

So, AC = 1.56m

Hence, the height of the arch at a point 1.5m from one end is approximately 1.56m.

5. A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.

Solution:

Let AB be the rod making an angle Ɵ with OX and P(x,y) be the point on it such that

AP = 3cm.

Diagrammatic representation is as follows:

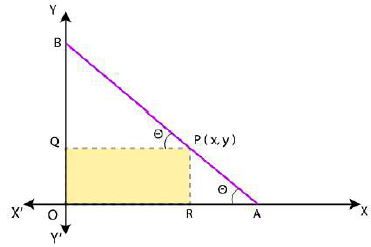
Then, PB = AB – AP = (12 – 3) cm = 9cm [AB = 12cm]

From P, draw PQ ⊥ OY and PR ⊥ OX.

In ΔPBQ, cos θ = PQ/PB = x/9

Sin θ = PR/PA = y/3

we know that, sin² θ +cos² θ = 1,

So,

(y/3)² + (x/9)² = 1 or

x²/81 + y²/9 = 1

Hence, the equation of the locus of point P on the rod is x²/81 + y²/9 = 1

6. Find the area of the triangle formed by the lines joining the vertex of the parabola x² = 12y to the ends of its latus rectum.

Solution:

The given parabola is x² = 12y.

On comparing this equation with x² = 4ay, we get,

4a = 12

a = 12/4

= 3

The coordinates of foci are S(0,a) = S(0,3).

Now let AB be the latus rectum of the given parabola.

The given parabola can be roughly drawn as

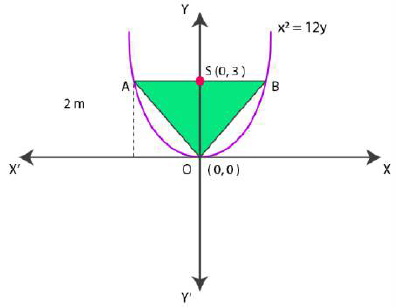
At y = 3, x² = 12(3)

x² = 36

x = ±6

So, the coordinates of A are (-6, 3), while the coordinates of B are (6, 3)

Then, the vertices of ΔOAB are O(0,0), A (-6,3) and B(6,3).

By using the formula,

Area of ΔOAB = ½ [0(3-3) + (-6)(3-0) + 6(0-3)] unit²

= ½ [(-6) (3) + 6 (-3)] unit²

= ½ [-18-18] unit²

= ½ [-36] unit²

= 18 unit²

∴ Area of ΔOAB is 18 unit²

7. A man running a racecourse notes that the sum of the distances from the two flag posts from him is always 10 m and the distance between the flag posts is 8 m.
Find the equation of the posts traced by the man.

Solution:

Let A and B be the positions of the two flag posts and P(x, y) be the position of the man.

So, PA + PB = 10.

We know that if a point moves in plane in such a way that the sum of its distance from two fixed point is constant, then the path is an ellipse and this constant value is equal to the length of the major axis of the ellipse.

Then, the path described by the man is an ellipse where the length of the major axis is 10m, while points A and B are the foci.

Now let us take the origin of the coordinate plane as the centre of the ellipse, and taking the major axis along the x- axis,

The diagrammatic representation of the ellipse is as follows:

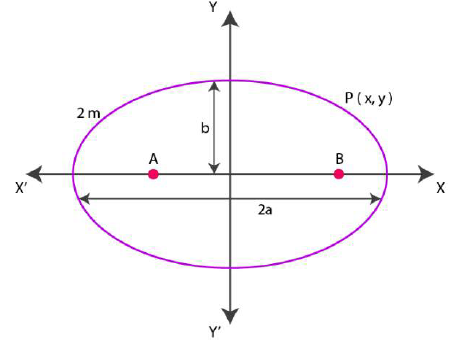
The equation of the ellipse is in the form of x²/a² + y²/b² = 1, where ‘a’ is the semi-major axis.

So, 2a = 10

a = 10/2

= 5

Distance between the foci, 2c = 8

c = 8/2

= 4

By using the relation, c = √(a² – b²), we get,

4 = √(25 – b²)

16 = 25 – b²

b² = 25 -1

= 9

b = 3

Hence, equation of the path traced by the man is x²/25 + y²/9 = 1

8. An equilateral triangle is inscribed in the parabola y² = 4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.

Solution:

Let us consider OAB be the equilateral triangle inscribed in parabola y² = 4ax.

Let AB intersect the x – axis at point C.

Diagrammatic representation of the ellipse is as follows:

Now let OC = k

From the equation of the given parabola, we have,

So, y² = 4ak

y = ±2√ak

The coordinates of points A and B are (k, 2√ak), and (k, -2√ak)

AB = CA + CB

= 2√ak + 2√ak

= 4√ak

Since, OAB is an equilateral triangle, OA² = AB².

Then,

k² + (2√ak)² = (4√ak)²

k² + 4ak = 16ak

k² = 12ak

k = 12a

Thus, AB = 4√ak = 4√(a×12a)

= 4√12a²

= 4√(4a×3a)

= 4(2)√3a

= 8√3a

Hence, the side of the equilateral triangle inscribed in parabola y² = 4ax is 8√3a.

Access Other Exercise Solutions of Class 11 Maths Chapter 11 – Conic Sections

Exercise 11.1 Solutions 15 Questions

Exercise 11.2 Solutions 12 Questions

Exercise 11.3 Solutions 20 Questions

Exercise 11.4 Solutions 15 Questions

Also explore – NCERT Class 11 Solutions